5. Методы измерений

При проведении измерений исходят из характера зависимости измеряемой величины от времени, вида уравнения измерений, условий, определяющих точность результата измерений и способов выражения этих результатов. По характеру зависимости измеряемой величины от времени измерения разделяются на: статические (измерения размеров тела, постоянного давления) при которых измеряемая величина остается постоянной во времени и динамические (измерение пульсирующих давлений, вибраций), при которых измеряемая величина изменяется и является непостоянной во времени. По способу получения результатов эти измерения разделяют на прямые и косвенные, совокупные и совместные.

Прямые - это измерения, при которых искомое значение физи­ческой величины находят непосредственно из опытных данных. Прямые измерения можно выразить формулой Q = Х, где Q - ис­комое значение измеряемой величины, а X - значение, непосред­ственно получаемое из опытных данных.

При прямых измерениях экспериментальным операциям под­вергают измеряемую величину, которую сравнивают с мерой не­посредственно или же с помощью измерительных приборов, гра­дуированных в требуемых единицах. Примерами прямых измере­ний служат измерения длины тела масштабной линейкой, массы при помощи весов и др. Прямые измерения широко применяются в машиностроении (измерения размерных параметров), а также при контроле технологических процессов (измерение давление температуры и др.).

Косвенные - это измерения, при которых искомую величину определяют на основании известной зависимости между этой ве­личиной и величинами, подвергаемыми прямым измерениям.

При косвенных измерениях измеряют не собственно определяе­мую величину, а другие величины, функционально с ней связан­ные. Значение измеряемой величины находят путем вычисления по формуле

Q = f (X₁, X₂, .. X_n)

где Q - искомое значение косвенно измеряемой величины; f -знак функциональной зависимости, форма которой и природа связанных ею величин заранее известны; X₁, X₂, .. X_n, - значения величин измеренных прямым способом.

Примерами косвенных измерений могут служить определение объема тела по прямым измерениям его геометрических размеров, нахождение удельного электрического сопротивления проводник, по его сопротивлению, длине и площади поперечного сечения.

Косвенные измерения широко распространены в тех случаях, когда искомую величину невозможно или слишком сложно изме­рить непосредственно или когда прямое измерение даст менее точ­ный результат. Роль косвенных измерений особенно велика при измерении величин, недоступных непосредственному эксперимен­тальному сравнению, например размеров астрономического пли внутриатомного порядка.

Совокупные - это производимые одновременно измерения не­скольких одноименных величин, при которых искомую величину определяют решением системы уравнений, получаемых при пря­мых измерениях различных сочетаний этих величин.

Примером совокупных измерений является определение мас­сы отдельных гирь набора (калибровка по известной массе од­ной из них по результатам прямых сравнений масс различных сочетаний гирь).

Совместные - это производимые одновременно измерения двух или нескольких неодноименных величин для нахождения зави­симостей между ними.

В качестве примера совместных измерений можно назвать из­мерение электрического сопротивления при 20°С и температурных коэффициентов измерительного резистора по данным прямых из­мерений его сопротивления при различных температурах.

По условиям, определяющим точность результата, измерения делятся на три класса.

1. Измерения максимально возможной точности, достижимой при существующем уровне техники.

К ним относятся в первую очередь эталонные измерения, свя­занные с максимально возможной точностью воспроизведения установленных единиц физических величин, и, кроме того, измере­ния физических констант, прежде всего универсальных (например, абсолютного значения ускорения свободного падения, гиромагнит­ного отношения протона и др.).

2. Контрольно-поверочные измерения, погрешность которых не должна превышать некоторое заданное значение.

К ним относятся измерения, выполняемые лабораториями государственного надзора за внедрением и соблюдением стандартов и состоянием измерительной техники и заводскими измерительны­ми лабораториями и осуществляемые такими средствами изме­рений и по такой методике, которые гарантируют погрешность результата, не превышающую некоторого, заранее заданного значения.

3. Технические измерения, в которых погрешность результата определяется характеристиками средств измерений.

Примерами технических измерений являются измерения, вы­полняемые в процессе производства на машиностроительных предприятиях, на щитах распределительных устройств электрических станций и др.

По способу выражения результатов измерений различают аб­солютные и относительные измерения.

Абсолютными называются измерения, которые основаны на прямых измерениях одной или нескольких основных величин или на использовании значений физических констант.

Примером абсолютных измерений может служить определение длины в метрах, силы электрического тока в амперах, ускорения свободного падения в метрах на секунду в квадрате.

Относительными называются измерения отношения величины к одноименной величине, играющей роль единицы, или измерения величины по отношению к одноименной величине, принимаемой за исходную.

В качестве примера относительных измерений можно при­вести измерение относительной влажности воздуха, определяемой как отношение количества водяных паров в 1 м³ воздуха к коли­честву водяных паров, которое насыщает 1 м³ воздуха при дан­ной температуре.

Все измерения основаны на физических закономерностях, определяющих принцип измерения. Для реализации тех или иных принципов измерения используют различные средства из­мерений.

Совокупность принципов и средств измерений, с помощью которых они осуществляются, составляют метод измерения.

Основными характеристиками измерений являются: принцип измерений, метод измерений, погрешность, точность, правильность и достоверность измерений.

Принцип измерений - физическое явление или совокупность физических явлений, положенных в основу измерений. Например, измерение массы тела при помощи взвешивания с использовани­ем силы тяжести, пропорциональной массе, измерение температу­ры с использованием термоэлектрического эффекта.

Метод измерения – это прием или совокупность приемов сравнения измеряемой ФВ с ее единицей в соответствии с реализованным принципом измерения. Методы измерения можно классифицировать по различным признакам.

Наиболее разработанной является классификация по совокупности приемов использования принципов и средств измерений. По этой классификации различают метод непосредственной оценки и методы сравнения.

Методы сравнения образуют группу: дифференциальный, нулевой, совпадений, замещения.

Метод непосредственной оценки позволяет получить значение величины непосредственно, без каких-либо до­полнительных действий и без вычислений. Исключением является умножение показаний на постоянную прибора или на цену деления. Чаще всего измерение с помощью этого метода осуществляется на показывающих прибо­рах: манометрах, динамометрах, жидкостных термомет­рах и т. д. Взвешивание грузов на циферблатных весах, измерение длины рулеткой - это тоже измерения мето­дом непосредственной оценки. Сущность метода непосредственной оценки состоит в том, что о значении измеряемой величины судят по показанию одного (прямые измерения) или нескольких (косвенные измерения) средств измерений, которые заранее проградуированы в единицах измеряемой величины или единиц других величин, от которых она зависит. В этом методе измеряемая величина определяется непосредственно по отсчетному устройству измерительного прибора, например взвешивание на циферблатных весах, измерение температуры жид­костным термометром, измерение давления манометром, определение времени с помощью секундомера, определение толщины детали с помощью микрометра или размера детали с помощью штангельциркуля, измерение давления пружинным манометром. Однако при этом точность измерения находится в пределах 2-3% в связи с влиянием различных внешних факторов на процесс измерения.

Дифференциальный (разностный) метод заключается в измерении разности между измеряемой величиной и величиной, значение которой известно. Использование этого метода дает возможность получать результаты с высокой точностью даже при применении сравнительно грубых приборов. При дифференциальном методе измерения на измерительный прибор (не обязательно прибор сравнения) подается непосредст­венно разность измеряемой величины и величины, воспроизводи­мой мерой. Этот метод может быть использован, конечно, только в тех случаях, когда просто и точно реализуется операция вычи­тания величин (длины, перемещения, электрические напряжения и Э.Д.С.). Дифференциальный метод не применим при измерении таких величин, как температура или твердость тел. При дифференциальном методе измеряемая величина Х сравнивается непосредственно или косвенно с величиной Х, воспроизводимой мерой. О значении величины Х судят по измеряемой прибором разности Х = Х_изм – Х_м.

Примером дифференциального метода может служить измерение вольтметром разности двух напряжений, из которых одно известно с большой точностью, а другое представляет собой искомую величину.

К разновидностям метода сравнения с мерой относится и ме­тод замещения, широко применяемый в практике точных метроло­гических исследований. Сущность метода заключается в том, что измеряемая величина замещается в измерительной установке не­которой известной величиной, воспроизводимой мерой. Замещение может быть полным или неполным, в зависимости от чего говорят о методе полного или неполного замещения. При полном замеще­нии показания не изменяются, и результат измерения принимается равным значению меры. При неполном замещении для получения значения измеряемой величины к значению меры следует приба­вить величину, на которую изменилось показание прибора. Таким образом, метод замещения заключается в поочередном измерении прибором искомой величины и выходного сигнала меры, однородного с измеряемой величиной. По результатам этих измерений вычисляется исходная величина. Поскольку оба измерения производятся одним и тем же прибором в одинаковых внешних условиях, а искомая величина определяется по отношению показаний прибора, погрешность результата измерения уменьшается в значительной мере

Преимущество метода замещения заключается в последовательномво времени сравнении измеряемой величины и величины, воспроизводимой мерой. Благодаря тому, что обе эти величины включаются одна за другой в одну и ту же часть измерительной цепи прибора, точностные возможности измерений значительно повышаются по сравнению с измерениями, проводящимися с по­мощью других разновидностей метода сравнения, где несимметрия цепей, в которые включаются сравниваемые величины, приводят к возникновению систематических погрешностей. Результат измерения либо вычисляют как сумму значения используемой для сравнения меры и показа­ния измерительного прибора, либо принимают равным значению меры.

Метод сравнения с мерой, заключающийся в том, что измеряе­мая величина и величина, воспроизводимая мерой, одновременно воздействуют на измерительный прибор сравнения, с помощью ко­торого устанавливается соотношение между ними, называется методом противопоставления. Примером этого метода является взве­шивание груза на равноплечих весах, когда измеряемая масса оп­ределяется как сумма массы гирь, ее уравновешивающих, и показа­ния по шкале весов.

При проведении наиболее точных измерений предпочтение от­дается различным модификациям метода сравнения с мерой, при котором измеряемую величину находят сравнением с величиной, воспроизводимой мерой. Примером этого метода является взве­шивание груза на равноплечих весах, когда измеряемая масса оп­ределяется как сумма массы гирь, ее уравновешивающих, и показа­ния по шкале весов.

Нулевой метод заключается в сравнении измеряемой величины с величиной, значение которой заранее изве­стно. Обе величины выбирают равными по размеру, та­ким образом, разность между ними будет равняться нулю. Метод состоит в том, что подбором раз­мера воспроизводимой мерой величины или путем ее принудитель­ного изменения эффект воздействия сравниваемых величин на при­бор сравнения доводят до нуля. В этом случае компенсация воз­действий влияющих величин оказывается более полной, а значение измеряемой величины принимается равным значению меры. Это контролируется специальным высокоточным прибором - нульиндикатором, что позволяет получить достаточно малую погрешность измерения.

Нулевой метод обладает высокой точностью, которая определяется точностью воспроизведения образцовой меры и чувствительностью нулевого прибора (например, метод измерений электрического сопротивления термометра уравнове­шенным мостом).

Нулевой метод применяют при взвешивании на лю­бых рычажных весах, когда масса гирь подбирается равной измеряемой массе. Высокие температуры изме­ряются с помощью оптического пирометра, принцип дей­ствия которого состоит в сравнении яркости нити нака­ливания электролампы с яркостью измеряемого фона (пламени, плавки, обжигаемых изделий). Накал нити регулируют до тех пор, пока яркость ее не сравняется с яркостью фона и нить как бы исчезнет. Таким образом, в оптическом пирометре используется нулевой метод из­мерения. Нулевой метод имеет много общего с дифференциальным; в дифференциальном методе измеряется разность между величинами, а в нулевом эта разность приводится к нулю.

В компенсационном методе измеряемую величину сравнивают с величиной воспроизводимой меры (например, измерение напряжения постоянного тока на компенсаторе сравнением с э.д.с. нормального элемента).

В методе совпадений разность между измеряемой величиной и величиной воспроизводимой мерой, определяют, используя совпадение отметок шкал или периодических сигналов. Этот метод широко используют в практике неэлектрических измерений. Метод используется в конструкции нониуса штангенциркуля, в электронно­лучевых трубках приборов для ультразвуковых испыта­ний материалов.

6. Погрешности измерений

При проведении измерений неизбежно возникают по­грешности, состоящие из погрешности инструменталь­ной и погрешности метода измерений, которые могут иметь систематические и случайные составляющие. Кро­ме того, в процессе измерения могут быть допущены про­махи или грубые погрешности.

Погрешность измерений - разность между полученным при измерении X' и истинным Q значениями измеряемой величины. Погрешность измерения Δ определяется формулой Δ = X' – Q

То есть под погрешностью измерений понимается алгебраическая разность между полученным при измерении значения измеряемой величины и значением, выражающим истинное значение этой величины, т.е. количественная близость измеренного и истинного значения измеряемой величины.

В этой формулировке есть одна неопределенность, связанная с тем, что никто не знает истинное значение измеряемой величины и под ним обычно понимают наиболее близкое к истинному значение. Истинное значение ФВ – это значение, идеальным образом отражающее свойство данного объекта, как в количественном, так и в качественном отношении. На практике это абстрактное понятие заменяют понятием действительное значение – это значение найденное экспериментально и настолько приближающаяся к истинному, что для данной цели оно может быть использовано вместо него. Результат измерения представляет собой приближенную оценку истинного значения величины, найденную путем измерения.

Погрешность измерений вызывается несовершенством методов и средств измерений, непостоянством условий наблюдения, а так­же недостаточным опытом наблюдателя или особенностями его органов чувств.

Как указывалось выше, точность измерений - это характери­стика измерений, отражающая близость их результатов к истинно­му значению измеряемой величины.

Количественно точность можно выразить величиной, обратной модулю относительной погрешности:

Например, если погрешность измерений равна 10^-2 % = 10^-4 то точность равна 10⁴.

Погрешность измерений выражают обычно в единицах измеряемой величины (абсолютная погрешность) или в долях (процентах) от ее значения (относительная погрешность).

По характеру и причинам появления погрешности, измерения относят к трем категориям – систематические, случайные и грубые погрешности измерения.

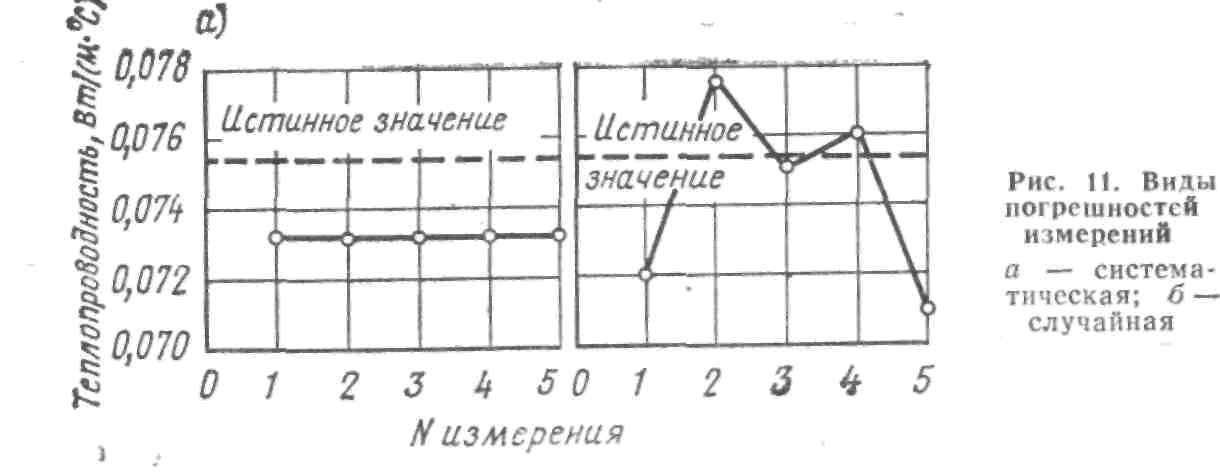Систематическими называют погрешности, которые в процессе последовательных измерений остаются постоян­ными или изменяются по определенному закону (рис. 7.1 а).

Рис. 7.1 Виды погрешностей измерения а) систематическая; б) случайная

Это составляющая часть общей погрешности измерений, остающаяся постоянной или изменяющаяся по определенному закону при повторных измерениях. Систематические погрешности могут быть изучены, а результат измерения уточнен путем введения поправок к показаниям измерительного устройства или применения других способов измерения, исключающих влияние систематических погрешностей [1].

Систематические погрешности могут быть определе­ны экспериментальным путем. Полученное значение погрешности вносят в виде поправки и тем самым улуч­шают результат измерения. Рассмотрим наиболее часто встречающиеся виды систематических погрешностей и способы их обнаружения.

Простейший пример систематической погрешности гири, на которой нанесено значение ее массы –1 кг, а истинная ее масса, при сравнении с эталоном, например, 999,5 г., т.е., при каждом взвешивании такой гирей будет вноситься абсолютная погрешность в 0,5 г.

Особенность систематических погрешностей в том, что они не зависят от числа измерений и поддаются в определенной степени учету (исключению). Они могут быть оценены экспериментально и внесены (учтены) в конечном результате измерения. Однако это касается систематических погрешностей, источник которых обнаружен.

По причинам возникновения систематические погрешности относятся к инструментальным, от неправильной установки измерительного устройства, вследствие внешних влияний, погрешности метода измерения и субъективные.

Инструментальными называют такие погрешности, причина которых заключается в особенностях средств измерения.

Точность измерения – характеристика качества измерения, отражающая близость к нулю погрешности его результата.

Сходимость результатов измерений – характеристика качества измерений, отражающая близость друг к другу результатов измерения одной и той же величины, выполняемые повторно одними и теми же методами и средствами измерений и в одних и тех же условиях. Сходимость измерений отражает влияние случайных погрешностей на результат измерения.

Воспроизводимость результатов измерений - характеристика качества измерений, отражающая близость друг к другу результатов измерения одной и той же величины, полученных в разных местах, разными методами и средствами измерения, разными операторами, но приведенных к одним и тем же условиям.

Правильность измерения определяется как качество измере­ния, отражающее близость к нулю систематических погрешностей результатов (т. е. таких погрешностей, которые остаются постоян­ными или закономерно изменяются при повторных измерениях од­ной и той же величины). Правильность измерений зависит, в част­ности, от того, насколько действительный размер единицы, в ко­торой выполнено измерение, отличается от ее истинного размера (по определению), т. е. от того, в какой степени были правильны (верны) средства измерений, использованные для данного вида измерений.

Важнейшей характеристикой качества измерений является их достоверность.

Достоверности измерения, характеризует степень доверия к результатам измерения и делит их на две категории: достоверные и недостоверные, в зависимости от того, известны или неизвестны вероятностные ха­рактеристики их отклонений от истинных значений соответствую­щих величин т.е. вероятные границы погрешности, за пределы которых не выходят результаты. Доверительная оценка достоверности результатов дается в процентах (90-95 %).

Инструментальные погрешности – это те систематические погрешности, которые зависят от того, какое средство измерения использовано для измерения. Источниками инструментальной погрешности могут быть:

- конструкция измерительного устройства;

(например, неравноплечность рычажных весов, затупление грани призмых весов, на которой уравновешивается коромысло, зазоры (люфты), в узлах трения механизмов прибора и трение в этих узлах, потери энергии в материале сердечников трансформаторов и т.д.)

• несовершенство или неточность в изготовлении прибора; (например, неточности допущенные при внесении градуировок шкал линеек, микрометров, потенциометров.

• вследствие износа, старения или неисправности измерительного устройства;

Например, равноплечие весы не могут быть идеально равноплечими, шкала прибора может быть неточно отградуирована, прибор подвергся пере­грузке - все это вызывает систематические погрешно­сти при измерениях.

Погрешности от неправильной установки средств измерений - возникает в том случае, когда установка прибора влияет на его точность (например, весов).

Погрешности от внешних влияний являются следствием не уточненных помех во внешней среде, которые по той или иной причине искажают результат измерений. Одним из распространенных источников погрешности за счет внешней среды является температура окружающей среды (особенно при неравномерном ее действии на объект).

Неблагоприятно влияет на точность измерения и циркуляция воздуха внутри помещения.

Теоретические погрешности связаны с погрешностя­ми самого метода измерения. Например, при измерении объема тел их форма принимается геометрически пра­вильной, и поэтому размеры измеряются в недостаточ­ном числе мест.

При использовании электрических влагомеров влаж­ность материалов определяется недостаточно точно. В данном случае причина погрешности связана с тем, что в основу измерений положен принцип упрощенной зависимости электрических параметров от влажности. На самом деле эти параметры зависят также от соста­ва и пористой структуры материалов.

Субъективные систематические погрешности являют­ся следствием индивидуальных качеств человека, обу­словленных особенностями его органов чувств или при­обретенными неверными навыками измерений.

Другими факторами, влияющими на точность измерения являются: магнитные и электрические поля, атмосферное давление, влажность воздуха и т.д.

Погрешности метода измерений (теоретические погрешности) связаны с тем, что одну и ту же величину иногда можно измерить разными способами (методами).

Субъективные систематические погрешности являются следствием индивидуальных особенностей человека, производящего измерения, его навыки в конкретном измерении, состояние его организма и т.д.

Способы исключения и учета систематических погрешностей могут быть сведены в четыре основные группы:

- устранение источников погрешностей до начала измерений (так называемая профилактика погрешно­стей);

- исключение погрешностей в процессе измерения разными способами: замещения, компенсации по знаку, противопоставления и т. д. (экспериментальное исклю­чение погрешностей);

- внесение известных поправок в результат изме­рения (исключение погрешностей вычислением);

- оценка границ систематических погрешностей, не поддающихся исключению.

Случайные погрешности. По теории вероятности случайным называют такое событие, которое при осуществлении определенного комплекса условий может произойти, а может и не происходить. Случайными называют такие погрешности, которые при повторных измерениях одной и той же величины принимают различные значения. Применительно к измерениям, даже когда они ведутся одним человеком и очень тщательно при их многократном повторении получают результаты, часть которых совпадает между собой, а другая в разной степени отличается от них (разброс результатов измерений).

Изучить и учесть случайные погрешности измерений помогает теория вероятностей и математическая статистика (в совокупности теория погрешностей).

При обработке результатов измерений, вычисляют среднее арифметическое ( _ср) суммы случайных погрешностей ряда измерений

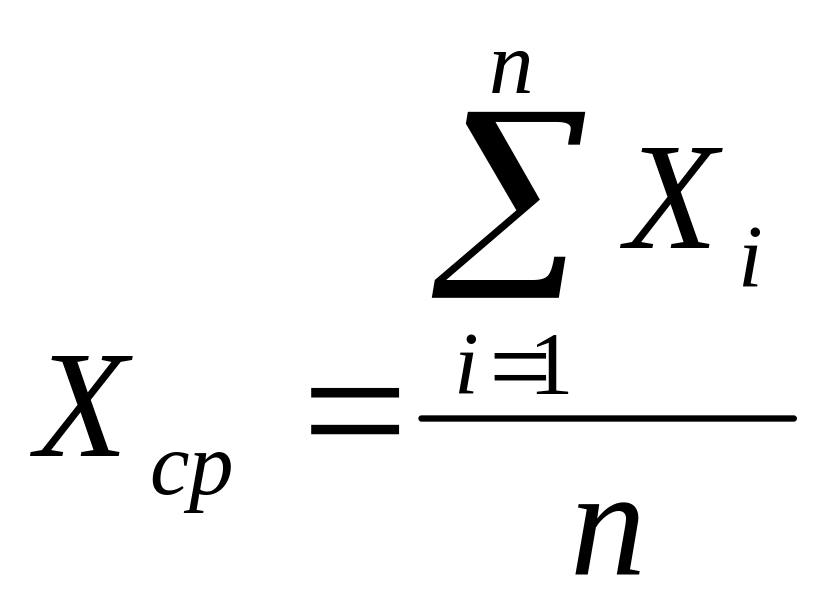
где Х_i – результат i измерения; n – число измерений.

Вычисляем отклонение от среднего значения по формуле

При этом необходимое иметь ввиду два важных свойства.

1. Алгебраическая сумма отклонений равна нулю

2. Сумма квадратов отклонений от среднего имеет минимальное значение

На основании проведенных вычислений определяют приближенное значение средней квадратичной погрешности по формуле

Грубые погрешности. Промахи (грубые погрешности) - это такие погреш­ности, которые значительно превышают объективно до­пустимые систематические или случайные погрешности. Промахи обычно возникают в результате ошибок наблю­дателя, а также вследствие неисправности приборов или резкого изменения условий измерения. К грубым погрешностям относят ошибки, допущенные человеком в процессе измерений, в частности:

• неправильный учет по шкале приборов (иногда из-за неверного учета цены малых делений);

• неправильная запись (описка) при занесении результата в журнал;

• внезапные и кратковременные изменения условий измерения;

• оставшиеся незамеченными неисправности прибора.

Грубые погрешности допускаются значительно реже, чем проявляются систематические и случайные и для их учета в большой массе измеренных величин также существуют специальные приемы.

С учетом всех категорий погрешностей, определяются показатели точности средств измерений, методы испытаний свойств веществ, являющихся объектами стандартизации [1].