2.2 Оценка устойчивости системы по критерию Найквиста

Критерий устойчивости Найквиста наиболее широко используется в инженерной практике по следующим причинам:

- устойчивость системы в замкнутом состоянии исследуют по частотной передаточной функции ее разомкнутой части W_раз(j), а эта функция, чаще всего, состоит из простых сомножителей. Коэффициентами являются реальные параметры системы, что позволяет выбирать их из условий устойчивости

- для исследования устойчивости можно использовать экспериментально полученные частотные характеристики наиболее сложных элементов системы, что повышает точность полученных результатов;

- устойчивость системы можно исследовать по логарифмическим частотным характеристикам, построение которых не сложно;

- достаточно просто определяются запасы устойчивости системы;

- удобно использовать для оценки устойчивости САР с запаздыванием.

Критерий Найквиста основан на анализе АФЧХ. Для построения АФЧХ необходимо определить АЧХ и ФЧХ.

W_раз(jω) = 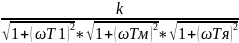= А(ω);

W_раз(jω) =

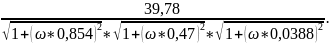
φ(jω) = arctg(jω) = (0^o+φ₁+φ₂+φ₃);

φ₁ = -arctg(ωT₁) = -arctg(ω*0,854);

φ₂ = -arctg(ωT_м) = -arctg(ω*0,47);

φ₃ = -arctg(ωT_я) = -arctg(ω*0,0388).

Таблица 2 – Данные для построения годографа Найквиста

ω	А(ω)	ϕ1	ϕ2	ϕ3	ϕ
0,00	39,78	0,00	0,00	0,00	0,00
0,61	33,90	-27,52	-16,00	-1,36	-44,87
1,49	20,10	-51,84	-35,00	-3,31	-90,15
3,30	7,15	-70,46	-57,19	-7,30	-134,95
9,36	1,03	-82,87	-77,19	-19,96	-180,02
32,00	0,06	-87,90	-86,20	-51,15	-225,25
45,00	0,02	-88,51	-87,29	-60,20	-236,00

Полученный годограф критерия Найквиста представлен на рисунке 5.

Рисунок 5 – Годограф Найквиста

Система неустойчива, так как годограф Найквиста охватывает точку(-1;0).

2.3 Исследование устойчивости по критерию Михайлова

Относится к частотным и основан на исследовании характерной функции D(jω)=U(ω)+jV(ω) полученной из характерного уравнения системы подстановкой p=jω.

Составим годограф функции:

D(p) = .

.

.

.

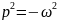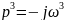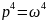D(jω) = .

Делим на действительную и мнимую части и находим значения при которых уравнения будут равны нулю:

= 0.

Действительная часть:

U(ω) =

.

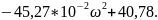
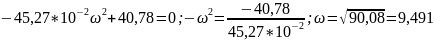Мнимая часть:

jV(ω) =

.

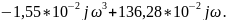
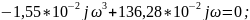
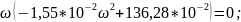
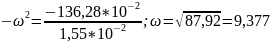Составляем таблицу 3 по результатам расчетов:

U(0) =

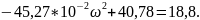
U(9,377) =

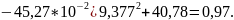
U(9,491) =

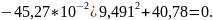
jV(0) =

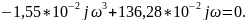
jV(9,377) =

jV(9,491) =

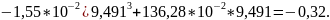
Таблица 3

ω	U(ω)	V(ω)
0	40,78	0,00
9,377	0,97	0,00
9,491	0,00	-0,32
∞	-∞	-∞

По данным таблицы 3 строим годограф Михайлова (рис. 6).

Рисунок 6 – годограф Михайлова

Система неустойчива, так как годограф проходит по часовой стрелки.