Лабораторная работа Моделирование гармонии Теоретическое введение

Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Гармоничная форма способствует наилучшему зрительному восприятию и появлению ощущения красоты. Под гармоничностью формы подразумевают пропорциональность основных размеров объекта и его составных частей, обеспечивающую зрительное восприятие объекта как единого целого. Еще древние греки заметили, что у гармоничных объектов простой формы коэффициент пропорциональности для сопоставляемых размеров одинаков и составляет приблизительно 1,62. У гармоничных объектов сложной формы коэффициенты пропорциональности могут варьироваться, но их значения имеют непосредственную связь с этим замечательным числом. Впоследствии это число получило название «золотое сечение» или «число Фибоначчи». Как получается это число?

Разделим отрезок АВ точкой С на две части так, чтобы отношение длины всего отрезка к длине его большей части равнялось отношению длины этой части к длине оставшейся: (Рис. 1). Обозначим длину всего отрезка АВ через d, а длину АС примем равной 1, тогда

.

Преобразуем это выражение

.

Найдем положительный корень полученного квадратного уравнения

Рис.1

Это иррациональное число и является знаменитым золотым сечением. Если мы прибавим к длине отрезка АВ длину его большей части АС, то отношение длины полученного отрезка к длине АВ снова будет равно d:

Эту процедуру можно продолжить до бесконечности, но пропорциональность отношения длины всего отрезка к длине его большей части не нарушится!

.

Знаменитый древнегреческий храм Парфенон, который считается одним из семи чудес античного мира, своей красотой поражает людей уже не одно тысячелетие. Своей гармоничной стройности он обязан тому, что соотношение его основных размеров, а также и размеров отдельных частей между собой определяется золотым сечением. Принцип золотого сечения используется архитекторами всего мира и по сей день [1].

Число d можно получить иначе. Итальянский математик Фибоначчи в 1202 году выстроил такой ряд целых чисел, в котором каждый его член, начиная с третьего, равен сумме двух предыдущих

1; 1; 2; 3; 5; 8; 13; 21; 34;…;(n); (n+1); ( (n)+ (n+1));…

Отношение каждого последующего члена ряда Фибоначчи к предыдущему является последовательным приближением к золотому сечению . Например, отношение шестого члена к пятому равно 8:5=1,6. А отношение девятого члена к восьмому: 34:21=1,61905.

Используя ряд Фибоначчи, можно получить значение d с любой степенью точности.

Я ркой иллюстрацией простой геометрической фигуры, вызывающей ощущение красоты и стройности, является правильная пятиконечная звезда (Рис. 2). Каждый луч этой звезды представляет собой равнобедренный треугольник, отношение боковой стороны которого к его основанию равно d. Каждый отрезок, соединяющий вершины звезды, поделен в пропорции золотого сечения так, что M:m=d.

О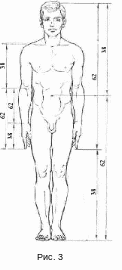 щущение гармоничности, которое вызывают у нас объекты с основными размерами, относящимися друг к другу в пропорции золотого сечения, не случайно. Пропорции человеческого тела напрямую связаны с золотым сечением. Немецкий исследователь профессор Цейзинг в 1854г. опубликовал труд [2], в котором на основании исследования двух тысяч человеческих тел пришел к выводу, что золотое сечение выражает средний статистический закон: отношение длины гармонично развитого человеческого тела к расстоянию от подошв до пояса равно золотому сечению. Пропорции золотого сечения проявляются и в отношении других частей тела, частей лица, кисти и т.д. (Рис. 3).

Пропорции золотого сечения часто встречаются и у представителей растительного и животного мира [3]. На рис. 4 изображен стебель цикория. Отростки делят длину стебля так, что отношение смежных частей равно d. На рис. 5 вы видите ящерицу. Размеры ее тела указаны в сантиметрах. Нетрудно найти и в отношениях этих чисел золотое сечение.

Многие великие умы волновала тайна золотого сечения. Им восхищались древнегреческий математик и философ Пифагор, великий художник и инженер Леонардо да Винчи, знаменитый астроном Кеплер и другие. И по сей день золотому сечению посвящают статьи и монографии математики и биологи [4], философы и искусствоведы [5,6]. Некоторые исследователи видят в золотом сечении выражение всеобщего закона гармонии природы [8]. С этим числом связывают и строение вселенной, и развитие жизнеобразующих форм, и пропорциональность структур в устойчивых сообществах, и многое, многое другое. Насколько они правы – это пока неясно, но несомненно одно: золотое сечение отражает особенности психологии восприятия человеком внешних образов. Поэтому принцип золотого сечения успешно используется для построения композиции произведения искусства и в музыке и в живописи и в литературе и в дизайне. Так, например, кульминационные события в романе никогда не происходят в середине повествования. В хорошем романе они сдвинуты ближе к концу, а отношение длины текста до кульминации к длине текста после нее равно золотому сечению.

Рис. 5	Рис. 4

В объектах сложной формы отношения размеров отдельных частей принимают различные значения, но данный объект воспринимается нами как гармоничный, пропорциональный, если эти отношения напрямую связаны с золотым сечением. На рис.6 представлен чертеж с анализом пропорций одного из красивейших зданий Петербурга – Смольного собора. В этом храме отношения между размерами отдельных частей равняются числу d, возведенному в разные степени.

Рис.6

Приведем пример графического построения отрезков, длины которых находятся в пропорции золотого сечения (Рис.7). Построим прямоугольный треугольник с катетом АВ, длина которого вдвое больше длины катета АС. Примем длину катета АС равной 1. Тогда длина катета АВ будет равна 2, а длина гипотенузы ВС равна 5. Продлим гипотенузу отрезком СD, длина которого равна 1. Разделим отрезок ВD точкой О пополам. Длина отрезка ВО равна (5+1):2=1,618…=d.

Построим на сторонах треугольника АВС прямоугольники: на стороне АВ прямоугольник, вторая сторона которого равна ВС; на стороне ВС прямоугольник, вторая сторона которого равна АС; на стороне АС прямоугольник, вторая сторона которого равна ВО (см. рис.7).

М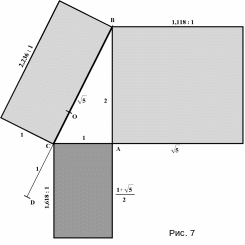 ы получили три прямоугольника, пропорции которых часто используются художниками при выборе размеров холста. Первый прямоугольник с отношением сторон 5:2=1,118:1 используется при написании погрудных портретов и натюрмортов. Художники его называют «живой квадрат». Этот прямоугольник зрительно воспринимается квадратом, если его длинная сторона горизонтальна. Второй прямоугольник с отношением сторон 2,236:1 называется «двойной квадрат» и используется при написании батальных сцен, панорамных пейзажей и парадных портретов во весь рост. Третий прямоугольник с отношением сторон, равным золотому сечению, особенно часто используется художниками. Они утверждают, что картина на холсте с такими пропорциями легко компонуется. Конечно, отношения сторон выдерживаются приблизительно, но отклонения, как правило, не больше 10%. Холсты с пропорциями других размеров используются сравнительно редко.

Выбирая холст того или иного размера, художник ориентируется на зрительное восприятие будущей картины, поэтому он сознательно или интуитивно стремится выбрать пропорции холста, обеспечивающие наиболее благоприятное впечатление. Напомним эти пропорции: 5:1; (5/2):1; d:1. Если учесть, что 5 входит в состав числа d, то все эти три пропорции непосредственно связаны с золотым сечением.