
Лекции по АиГ / Alg_13
.docМногочлены и функции от оператора.
Пусть j: Vk® Vk линейный оператор, a0+a1x+…+amxm = p(x) – многочлен над полем k.
Определение.
Положим: p(j) = a0idV+a1j+…+amjm. Оператор p(j): Vk® Vk называется многочленом от оператора j. Если V конечномерно, e – базис V и A = Ae(j) – матрица оператора в этом базисе, то, очевидно, Ae(p(j)) = a0E+a1A+…+amAm. Эта матрица обозначается p(A) и называется многочленом от матрицы A.
Отметим, что по формуле замены базиса p(S-1AS) = S-1p(A)S.
Поскольку степени одной матрицы коммутируют между собой, для любых многочленов p и q имеет место формула: p(A)q(A) = q(A)p(A). Точно также коммутируют и операторы p(j) и q(j).
Теорема.
Собственный вектор v оператора j, отвечающий собственному значению l, является собственным и для оператора p(j), причем соответствующее собственное значение равно p(l).
Доказательство.
Из равенства j(v) = lv индукцией по k выводим равенство jk(v) = lkv. Отсюда следует, что p(j)v = (a0id+a1j+…+amjm)v = a0v+a1lv+…+amlmv = p(l)v.
Лемма.
Пусть A
– квадратная матрица, имеющая блочный
вид
![]() ,
где матрицы B
и C
квадратные, а элементы, обозначенные
звездочкой, не играют роли. Тогда для
всякого многочлена p
имеем:
,
где матрицы B
и C
квадратные, а элементы, обозначенные
звездочкой, не играют роли. Тогда для
всякого многочлена p
имеем:
![]() .
.
(Индукцией
по k
выводится равенство
![]() ,
после чего утверждение становится
очевидным).
,
после чего утверждение становится
очевидным).
Следствие.
Если A = diag(l1,l2, …ln), то p(A) = diag(p(l1), p(l2), …p(ln)). Если A – верхняя треугольная матрица с диагональными элементами l1,l2, …ln, то p(A) – также верхняя треугольная с диагональными элементами p(l1), p(l2), …p(ln).
Теорема Гамильтона-Кэли.
Каждая квадратная матрица A является корнем своего характеристического многочлена, то есть pA(A) = 0.
Доказательство.
Будем
считать, что элементы матрицы A
лежат в поле kÌC
и
порядок A
равен n.
Рассмотрим линейный оператор j:
Cn®
Cn,
действующий по формуле: j(x)
= Ax.
Тогда A = Ae(j),
где e
– стандартный базис пространства Cn.
Проведем индукцию по n.
Если n
= 1 и A = (a),
то pA(x)
= a-x
и потому pA(A)
= a-a
= 0. Пусть результат уже доказан для
матриц порядка (n-1)
и A
имеет порядок n.
Характеристический многочлен pA(x)
по теореме Гаусса имеет в поле C
корень
l.
Пусть h1
– собственный вектор оператора j,
относящийся к собственному значению
l.
Включим вектор h1
в некоторый базис h =
(h1,…, hn)
пространства Cn.
Матрица B = Ah(j)
имеет вид:
![]() ,
где CÎMat(n-1)´(n-1)(C).
Раскладывая определитель det(B-xE)
по первому столбцу, приходим к равенству:
pB(x)
= (l-x)pC(x).
По предположению индукции pC(C)
= 0. Используя лемму, получаем:
,
где CÎMat(n-1)´(n-1)(C).
Раскладывая определитель det(B-xE)
по первому столбцу, приходим к равенству:
pB(x)
= (l-x)pC(x).
По предположению индукции pC(C)
= 0. Используя лемму, получаем:
![]() .
Но тогда pB(B)
= (lE-B)pC(B)
=
.
Но тогда pB(B)
= (lE-B)pC(B)
=
![]() .
Поскольку A
и B
– матрицы одного оператора в разных
базисах, имеем A = S-1BS
и pA(x)
= pB(x).
Следовательно, pA(A)
= pB(A)
= pB(S-1BS)
= S-1pB(B)S
= 0, что и требовалось доказать.
.
Поскольку A
и B
– матрицы одного оператора в разных
базисах, имеем A = S-1BS
и pA(x)
= pB(x).
Следовательно, pA(A)
= pB(A)
= pB(S-1BS)
= S-1pB(B)S
= 0, что и требовалось доказать.
Следствие 1.
Для любого оператора в конечномерном пространстве справедливо равенство: pj(j) = 0.
Следствие 2.
Если два многочлена p1 и p2 совпадают на спектре S матрицы A, то p1(A) = p2(A).
В самом деле, если (p1-p2)|S = 0, то pA|(p1-p2). Записывая p1-p2 = pAr, получаем: p1(A)-p2(A) = pA(A)r(A) = 0.
Замечание.
В процессе
доказательства было показано, что всякая
матрица A
с комплексными элементами подобна
матрице вида
![]() ,
где l
- одно из ее собственных значений. Отсюда
по индукции получается, что A
подобна верхней
треугольной матрице
,
где l
- одно из ее собственных значений. Отсюда
по индукции получается, что A
подобна верхней
треугольной матрице
 ,
причем набор l1,…,ln
совпадает со спектром матрицы A.
Значит, согласно следствию к предыдущей
теореме, спектр матрицы p(A)
совпадает с набором p(l1),…,
p(ln).
Отметим, в частности, что det
p(A) =
p(l1)…p(ln).
,
причем набор l1,…,ln
совпадает со спектром матрицы A.
Значит, согласно следствию к предыдущей
теореме, спектр матрицы p(A)
совпадает с набором p(l1),…,
p(ln).
Отметим, в частности, что det
p(A) =
p(l1)…p(ln).
Примеры.
-
Если для квадратной матрицы A порядка n существует такое число N, что AN = 0, то матрица A называется нильпотентной, а наименьшее число N в последнем равенстве – показателем ее нильпотентности. Единственная матрица с показателем нильпотентности 1 – нулевая матрица. Легко проверить, что матрица
 при p ¹
0 имеет показатель нильпотентности 2.
Заметим, что все корни характеристического
многочлена нильпотентной матрицы равны
0. В самом деле, если lÎC
один из его корней и vÎCn
соответствующий собственный вектор,
то ANv
= lNv
= 0 и потому l
= 0. Следовательно, pA(x)
= xn.
По теореме Гамильтона-Кэли отсюда
следует, что An
= 0. Итак, показатель нильпотентности
матрицы не может превосходить ее
порядка.
при p ¹
0 имеет показатель нильпотентности 2.
Заметим, что все корни характеристического
многочлена нильпотентной матрицы равны
0. В самом деле, если lÎC
один из его корней и vÎCn
соответствующий собственный вектор,
то ANv
= lNv
= 0 и потому l
= 0. Следовательно, pA(x)
= xn.
По теореме Гамильтона-Кэли отсюда
следует, что An
= 0. Итак, показатель нильпотентности
матрицы не может превосходить ее
порядка. -
Пусть для матрицы
 найден характеристический многочлен
pA(x)
= -x3+x2+3x-1.
По теореме Гамильтона-Кэли имеем
E = 3A+A2-A3.
Поскольку pA(0)
= det A = -1 ¹
0, обратная матрица A-1
существует. Умножая предыдущее равенство
на A-1,
получаем: A-1 =
3E+A-A2.
Матрицу A2
находим непосредственно: A2
=
найден характеристический многочлен
pA(x)
= -x3+x2+3x-1.
По теореме Гамильтона-Кэли имеем
E = 3A+A2-A3.
Поскольку pA(0)
= det A = -1 ¹
0, обратная матрица A-1
существует. Умножая предыдущее равенство
на A-1,
получаем: A-1 =
3E+A-A2.
Матрицу A2
находим непосредственно: A2
=
 .
Отсюда получаем: A-1
=
.
Отсюда получаем: A-1
=
 .
Можно найти также степени A3,
A4,
и т.д. не перемножая матрицы. В
самом
деле,
A3 =
A2+3A-E
=
.
Можно найти также степени A3,
A4,
и т.д. не перемножая матрицы. В
самом
деле,
A3 =
A2+3A-E
=
 ,
A4 =
A3+3A2-A
=
,
A4 =
A3+3A2-A
=
 и
т.д.
и
т.д. -
Как вычислить
 ?
Спектр матрицы имеет вид 1[2].
Пусть p1(x)
= x100, p2(x)
= 100x-99.
Тогда p1(1) =
p2(1),
?
Спектр матрицы имеет вид 1[2].
Пусть p1(x)
= x100, p2(x)
= 100x-99.
Тогда p1(1) =
p2(1),
 ,
то есть эти многочлены равны на спектре
матрицы A.
Значит, A100 =
p1(A)
= p2(A)
= 100A-99E =
,
то есть эти многочлены равны на спектре
матрицы A.
Значит, A100 =
p1(A)
= p2(A)
= 100A-99E =
 .
.
Отметим, что в последнем примере p2(x) – интерполяционный многочлен Лагранжа-Сильвестра для таблицы значений функции x100 на спектре матрицы.
Пусть теперь j: VC® VC – любой оператор, S - его спектр и f(z) – такая функция комплексного переменного z, которая определена на S, то есть в простых точках S существуют значения этой функции, а в точке спектра кратности k - еще и ее производные до порядка (k-1). Составим таблицу значений T функции f на спектре.
Определение.
Пусть функция f(z) определена на спектре S матрицы A и T – таблица ее значений на S. Построим по этим значениям интерполяционный многочлен p(z). Определим тогда значение функции от оператораj формулой: f(j) = p(j).
Замечание 1
Если имеются 2 интерполяционных многочлена p1 и p2, построенных по значениям одной функции f(z), то, поскольку p1(S) = p2(S), имеем p1(j) = p2(j), так что оператор f(j) определен однозначно.
Замечание 2.
Если VC конечномерно, e – базис этого пространства и A = Ae(j), то матрица f(A) определяется формулой f(A) = p(A), где p – многочлен, интерполирующий значения f(z) на спектре матрицы A. Очевидно, f(A) = Ae(f(j)). Поэтому f(S-1AS) = S-1f(A)S.
Примеры.
-
Пусть
 ,
f(z) =
,
f(z) =
 .
Спектр A
имеет вид: 1, 4. Таблица значений функции
на спектре имеет вид
.
Спектр A
имеет вид: 1, 4. Таблица значений функции
на спектре имеет вид
-
z
1
4
f(z)
±1
±2
Двойные
знаки во второй строке таблицы отражают
тот факт, что f(z)
– многозначная функция и потому для
выбора в каждом столбце таблицы одного
из ее двух значений необходимы
дополнительные соглашения. Будем
считать, что мы хотим найти значения
всех 4 функций на матрице A.
Соответствующие интерполяционные
многочлены равны: p+,+
= 1/3(x+2); p+,-
= -x+2; p-,+
= x-2; p-,-
= -1/3(x+2).
Соответственно получаем 4 значения
корня из матрицы:
![]() .
Проверка
показывает, что квадрат любой из этих
матриц равен A.
.
Проверка
показывает, что квадрат любой из этих
матриц равен A.
-
Пусть V – пространство многочленов степени не выше n и D – оператор дифференцирования в этом пространстве. Построим оператор ehD, где hÎC некоторое число. Выберем базис e = (1,x, …,xn) пространства V. Поскольку Dxm = mxm-1, матрица оператора в этом базисе будет верхней треугольной с нулями на главной диагонали. Следовательно, все собственные значения оператора равны 0 и его спектр имеет вид 0[n+1]. Интерполяционный многочлен Лагранжа-Сильвестра, построенный по значениям функции ehz на спектре, совпадает с многочленом Тейлора: p(z) = 1+hz+h2z2/2!+…=hnzn/n! Поэтому ehD = id+hD+…+hnDn/n! Если qÎV – любой многочлен, то ehDq(z) =
 = q(z+h).
Итак, ehD
– оператор сдвига на число h.
= q(z+h).
Итак, ehD
– оператор сдвига на число h.
Замечание.
Если функция f(z) принимает действительные значения при zÎR, а оператор j переводит вещественные векторы в вещественные, то можно доказать, что таким же свойством будет обладать и оператор f(j). Аналогично, если A – матрица с вещественными элементами, то такой же будет и матрица f(A).
Теорема
Если между функциями f1(z), …fn(z) имеется алгебраическая зависимость U(f1,…fn) = 0, где U(x1,…, xn) – некоторый многочлен от n неизвестных, то такая же зависимость имеется между операторами f1(j),…, fn(j): U(f1(j),…, fn(j)) = 0.
Доказательство.
Отметим,
прежде всего, что поскольку операторы
f1(j),…,
fn(j)
коммутируют между собой, выражение
U(f1(j),…,
fn(j))
имеет смысл. (Иначе, например для U
= x1x2
= x2x1,
пришлось бы различать операторы
f1(j)f2(j)
и f2(j)f1(j)).
Пусть p1(z),…,
pn(z)
– многочлены, интерполирующие значения
функций f1(z),…,
fn(z)
на спектре S.
Проверим, что многочлен p(z)
= U(p1(z),…,
pn(z))
равен 0 на спектре S.
Если l
- точка спектра кратности k,
то надо проверить, что значения функции
p,
а также ее производных до порядка (k-1)
включительно в этой точке равны 0. Как
известно, производная порядка p
от сложной функции U(g1(z),…,
gn(z))
представляет собой многочлен от частных
производных внешней функции
![]() и производных
и производных
![]() внутренних функций, причем s£p.
Поскольку для функций f(z)
= U(f1(z),…,
fn(z))
º
0 и p(z)
внешние функции совпадают, а внутренние
имеют одинаковые производные до порядка
(k-1)
по определению интерполяционного
многочлена, мы видим, что действительно
p(S)
= f(S)
= 0. Следовательно, по определению, f(j)
= p(j)
= 0, что и требовалось.
внутренних функций, причем s£p.
Поскольку для функций f(z)
= U(f1(z),…,
fn(z))
º
0 и p(z)
внешние функции совпадают, а внутренние
имеют одинаковые производные до порядка
(k-1)
по определению интерполяционного
многочлена, мы видим, что действительно
p(S)
= f(S)
= 0. Следовательно, по определению, f(j)
= p(j)
= 0, что и требовалось.
Примеры.
-
Доказанная теорема объясняет, почему в примере 1 предыдущего раздела мы действительно построили корни из матрицы. Вот еще один аналогичный пример. Пусть требуется найти решение матричного уравнения 2X3+3X = A, где
 .
Рассмотрим алгебраическое уравнение
2x3+3x
= t.
Пусть x(t)
– один из его корней. Поскольку
2x3(t)+3x(t)-t
º
0, (1) доказанная теорема позволяет
утверждать, что функция x(A)
будет одним из решений исходного
матричного уравнения. Чтобы найти эту
матрицу надо составить таблицу значений
x(t)
на спектре A.
Легко проверить, что спектр A
имеет вид 5[2].
Следовательно, нам надо найти x(5)
и
.
Рассмотрим алгебраическое уравнение
2x3+3x
= t.
Пусть x(t)
– один из его корней. Поскольку
2x3(t)+3x(t)-t
º
0, (1) доказанная теорема позволяет
утверждать, что функция x(A)
будет одним из решений исходного
матричного уравнения. Чтобы найти эту
матрицу надо составить таблицу значений
x(t)
на спектре A.
Легко проверить, что спектр A
имеет вид 5[2].
Следовательно, нам надо найти x(5)
и
 .
Уравнение 2x3+3x
= 5 имеет действительный корень x1
= 1 и два комплексных корня: x2,3
= 0,5(-1±3I).
Положим x(5)
= 1. Чтобы найти производную
.
Уравнение 2x3+3x
= 5 имеет действительный корень x1
= 1 и два комплексных корня: x2,3
= 0,5(-1±3I).
Положим x(5)
= 1. Чтобы найти производную
 продифференцируем соотношение (1):
продифференцируем соотношение (1):
 .
Отсюда
.
Отсюда
 =
1/9. По этим значениям построим
интерполяционный многочлен L1(t)
= 1/9(t+4).
Следовательно, x(A)
= L1(A)
= 1/9
=
1/9. По этим значениям построим
интерполяционный многочлен L1(t)
= 1/9(t+4).
Следовательно, x(A)
= L1(A)
= 1/9 .
Аналогично, по значениям x2,3
можно построить еще 2 комплексных
решения того же уравнения:
.
Аналогично, по значениям x2,3
можно построить еще 2 комплексных
решения того же уравнения:
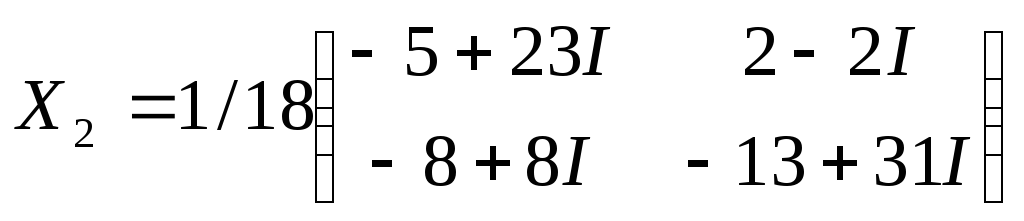 и
и
 .
. -
Соотношения e(p+q)z = epzeqz и sin2z+cos2z = 1 приводят к соотношениям между соответствующими операторами или матрицами: e(p+q)A = epAeqA и sin2A+cos2A = E. В то же время соотношение eA+B = eAeB может и не выполняться для произвольных матриц A и B, поскольку тождество ex+y = exey нельзя записать в виде соотношения U(f1(z), f2(z)) = 0.
