Лекции по АиГ / Alg_11

Линейные операторы (продолжение).

Собственные векторы и собственные значения линейного оператора.

Определение.

Пусть j: U_k® U_k линейный оператор. Вектор uÎU называется собственным вектором, а скаляр lÎk собственным значением оператора j, если

1. u ¹ 0;

2. j(u) = lu.

Отметим, что, поскольку u ¹ 0, скаляр l определен однозначно.

Примеры.

1. Пусть U – пространство геометрических векторов , mÌR³ некоторая прямая. Определим в пространстве U оператор j формулой: j(x) = пр_mx. Поскольку пр_m(x+y) = пр_mx+пр_my и пр_m(lx) = lпр_mx, оператор j будет линейным. Если x½½m, то j(x) = x = 1x так что x будет собственным вектором, относящимся к собственному значению l = 1. Если x ^ m, то j(x) = 0 = 0x и такой вектор будет собственным, относящимся к собственному значению l = 0.

2. Для нулевого оператора O: U® U любой вектор x ¹ 0 будет собственным и соответствующее собственное значение равно 0. Точно также для тождественного оператора id: U® U все ненулевые векторы – собственные и l = 1.

3. Пусть U = C^¥(R ) – пространство бесконечно дифференцируемых функций на оси, ¶: U® U оператор дифференцирования. Равенство имеет место в точности для показательных функций: f(t) = Ce^lt так что при C ¹ 0 такая функция будет собственным вектором оператора дифференцирования, относящимся к собственному значению l.

Случай конечномерного пространства.

В случае конечномерного пространства U можно указать способ нахождения собственных векторов и собственных значений линейного оператора.

Теорема.

Пусть j: U_k® U_k линейный оператор в пространстве размерности n, A = A_e(j) матрица этого оператора в некотором базисе e. Тогда:

1. Функция P_A(x) = det(A-xE) является многочленом степени n. Этот многочлен не зависит от выбора базиса e и называется характеристическим многочленом линейного оператора j.

2. Скаляр lÎk будет собственным значением оператора тогда и только тогда, когда P_A(l) = 0.

3. Ненулевой вектор xÎU будет собственным для j и ему отвечает собственное значение l тогда и только тогда, когда (A-lE)x_e = 0.

Доказательство.

Матрица B = A-xE является квадратной порядка n, все элементы которой, за исключением диагональных, равны соответствующим элементам матрицы A, а диагональные элементы равны (a_ii-x). Поэтому каждый член в разложении ее определителя представляет собой многочлен от x степени не выше n, причем только один из них - а именно b₁₁…b_nn = (a₁₁-x)…(a_nn-x) имеет степень n. Следовательно, detB – многочлен от x вида: (-1)ⁿxⁿ+… Если h – другой базис в U, то A_h(j) = S^-1AS, а потому

Det(A_h(j)-xE) = detS^-1det(A-xE)detS = det(A-xE).

Если x собственный вектор j, относящийся к собственному значению l, то Ax_e = lx_e или (A-lE)x_e = 0. Отсюда можно сделать вывод, что однородная система линейных уравнений (A-lE)y = 0 имеет ненулевое решение и потому ее определитель равен 0, что можно записать как P_A(l) = 0. Тем самым все утверждения теоремы доказаны.

Фиксируем некоторое собственное значение lÎk. Множество всех векторов, координаты которых удовлетворяют системе уравнений (A-lE)x_e = 0, образуют подпространство U_l = Ker(j-lid) положительной размерности, называемое подпространством собственных векторов, относящихся к собственному значению l. Если dim U_l = g, то можно выбрать линейно независимую систему из g собственных векторов, относящихся к этому собственному значению. Число g = g(l) называется геометрической кратностью собственного значения l.

Теорема.

Пусть l - одно из собственных значений оператора j в конечномерном пространстве, так что l корень характеристического многочлена. Пусть (алгебраическая) кратность этого корня равна a = a(l). Тогда g(l)£a(l).

Доказательство.

По условию теоремы можно выбрать линейно независимую систему, состоящую из g собственных векторов оператора, относящихся к собственному значению l. Дополним эту систему до базиса e всего пространства. Поскольку j(e_i) = le_i при i = 1, 2,…, g, матрица A оператора в этом базисе имеет вид A = . Раскладывая определитель det(A-xE), а затем полученные миноры по первому столбцу, получим: P_A(x) = (l-x)^g det(D-xE). Отсюда вытекает, что (x-l)^g | P_A(x), что и требовалось доказать.

Линейно независимые системы собственных векторов.

Теорема 1.

Пусть j - линейный оператор, l₁, …, l_k – попарно различные собственные значения этого оператора, x₁,…, x_k – соответствующие собственные векторы. Тогда эти векторы линейно независимы.

Доказательство.

Предположим, что m₁x₁+…+m_kx_k = 0. Докажем, что все векторы y_i = m_ix_i нулевые, откуда и будет следовать наше утверждение, поскольку x_i ¹ 0.

По предположению:

y₁+…+y_k = 0. (0)

Применим к обеим частям этого равенства оператор j. С учетом того, что j(y_i) = l_Iy_i, получим:

l₁y₁+…+l_ky_k = 0 (1)

Если снова применить оператор j, то получится аналогичное равенство с заменой l_i на (l_i)². Применяя оператор j s раз, получим равенство:

= 0 (s).

Пусть q(x)Îk[x] – любой многочлен, q(x) = q₀+q₁x+…+q_mx^m. Если равенство (0) умножить на q₀, равенство (1) – на q₁ и т.д. равенство (m) на q_m и все эти равенства сложить, то получится: q(l₁)y₁+…+q(l_k)y_k = 0. Выберем такой многочлен q, для которого все числа l₁,…, l_k, за исключением l_i являются корнями (например, q(x) =). Тогда получим: q(l_i)y_i = 0, а так как i может быть любым, это и доказывает наше утверждение.

Теорема 2.

Пусть в условиях предыдущей теоремы для каждого собственного значения l_i выбрана линейнонезависимая система S_i, состоящая из собственных векторов оператора, относящихся к этому собственному значению. Тогда система S = S₁È…ÈS_k линейно независима.

Доказательство.

Пусть . Обозначим через y_i вектор равный , так что y₁+…+y_k = 0. Поскольку вектор y_i лежит в подпространстве собственных векторов, относящихся к собственному значению l_i, рассуждение, использованное при доказательстве теоремы 1, показывает, что этот вектор нулевой. Но тогда = 0 и виду линейной независимости системы S_i, все коэффициенты m_a = 0 при x_aÎS_i. Так как i может быть любым, отсюда и следует утверждение теоремы.

Следствие.

Пусть j - линейный оператор в конечномерном пространстве U_k, l₁,…, l_k – полное множество его попарно различных собственных значений, g_i = g(l_i) – их геометрическая кратность. Тогда максимальная линейно независимая система, состоящая из собственных векторов этого оператора, содержит g₁+…+g_k векторов.

Приведение линейного оператора к диагональному виду.

В этом разделе будут изучаться исключительно операторы в пространстве конечной размерности n.

Теорема.

Матрица линейного оператора j в базисе e имеет диагональный вид D, тоесть равна 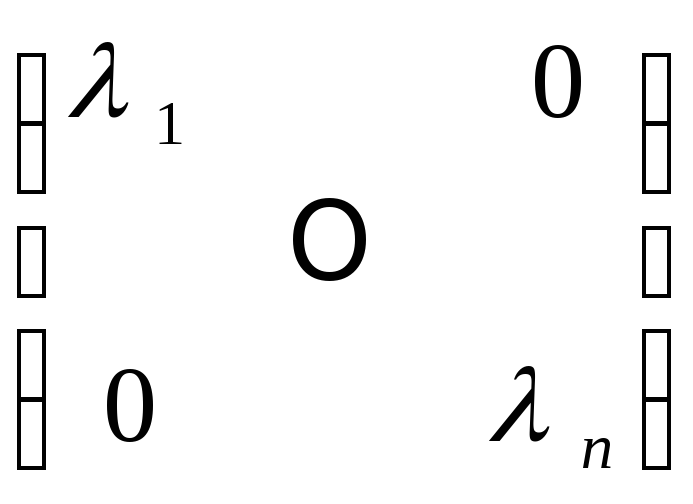= diag(l₁,…, l_n) тогда и только тогда, когда e состоит из собственных векторов этого оператора. При этом диагональные элементы l₁,…, l_n равны соответствующим собственным значениям.

Доказательство.

Пусть e_k – собственный вектор оператора, относящийся к собственному значению l_k, так что j(e_k) = l_ke_k. Поскольку c_k(A_e(j)) = j(e_k)_e = , мы получаем, что A_e(j) = diag(l₁,…, l_n). Обратно, если матрица оператора диагональна, то j(e_k) = ej(e_k)_e = l_ke_k. Поскольку базис не может содержать нулевых векторов, мы видим, что e_k – собственный вектор оператора, относящийся к собственному значению l_k.

Говорят, что линейный оператор j в пространстве U приводится к диагональному виду, если существует базис, в котором матрица этого оператора имеет диагональный вид. Доказанная теорема утверждает, что такое приведение возможно в точности тогда, когда из собственных векторов оператора можно построить базис пространства U.

Определение.

Спектром квадратной матрицы AÎMat_n´n(C ) называется набор корней характеристического многочлена P_A(x), указанных вместе с их алгебраическими кратностями.

Если kÌC это определение пригодно и для матриц с элементами из k, но в этом случае сами точки спектра уже могут и не входить в поле k. Поскольку над полем комплексных чисел многочлен степени n имеет ровно n корней, если каждый из них учитывать столько раз, какова его кратность, то k₁+…+k_s = n.

Так как характеристический многочлен матрицы линейного оператора не зависит от выбора базиса, можно говорить о спектре линейного оператора.

Теорема (о приведении оператора к диагональному виду).

Линейный оператор j: U_k® U_k приводится к диагональному виду тогда и только тогда, когда

1. Все точки спектра оператора лежат в поле k.

2. Для всякой точки спектра l_i ее алгебраическая кратность равна геометрической: k(l_i) = k_i = g_i = g(l_i).

Доказательство.

Оператор приводится диагональному виду тогда и только тогда, когда в пространстве U_k можно построить базис из его собственных векторов, то есть линейно независимую систему, состоящую из n = dim U_k собственных векторов. Пусть - собственные значения оператора, указанные вместе с кратностями равных им корней характеристического многочлена. Тогда k₁+…+k_p£ n, причем равенство имеет место в точности тогда, когда все корни характеристического многочлена лежат в поле k. Поскольку геометрическая кратность не выше алгебраической, имеем:

m =g₁+…+g_p£ k₁+…+k_p£ n.

Как нам известно, m – количество векторов в максимальной линейно независимой системе собственных векторов оператора. Мы видим, что равенство m = n имеет место тогда и только тогда, когда выполнены условия 1) и 2), указанные в теореме.

Замечание.

Если k(l_i) = 1, то, поскольку 0< g(l_i)£ k(l_i), имеем: k(l_i) = g(l_i). Значит, если спектр оператора простой, то есть все кратности k(l_i) = 1, то условие 2) выполняется автоматически. Условие 1) не нуждается в проверке, если k = C Итак, всякий оператор над полем C с простым спектром приводится к диагональному виду.

Пример.

Пусть a,bÎk. В пространстве k_n[x] многочленов степени не выше n рассмотрим оператор j_a,b, действующий по формуле: j_a,b(p(x)) = p(ax+b). Выясним, при каких значениях параметров a, b этот оператор приводится к диагональному виду. Выберем базис e из многочленов p₀ = 1, p₁ = x,…, p_n = xⁿ. Поскольку (ax+b)^k = , матрица A = A_e(j) будет верхней треугольной с элементами при i£ j; i,j = 0, 1,…, n. На диагонали этой матрицы расположены элементы 1, a, a²,…, aⁿ, которые и составляют спектр этого оператора. Отметим, что все точки спектра лежат в поле k. Если среди этих чисел нет одинаковых, то спектр оператора прост и потому оператор приводится к диагональному виду. Это условие будет выполнено при a ¹ 0 и a^k ¹ 1 при 1< k£ n. Базис из собственных векторов составляют при этом многочлены q_k = (x+b/(a-1))^k, k = 0,…, n. В самом деле,

j(q_k) = (ax+b+b/(a-1))^k = a^k(x+b/(a-1))^k. Если a^k = 1, но a ¹ 1, то те же многочлены составляют базис из собственных векторов, так что оператор и в этом случае приводится к диагональной форме, хотя его характеристический многочлен и имеет кратные корни. Оставляем читателю проверку условия 2) в этом случае. При a = 0 спектр оператора имеет вид 1^[1], 0^[n], а в матрице A все строки, начиная со второй – нулевые. Поэтому g(0) = (n+1)-rkA = n = a(0) и условие 2) снова выполнено. Оператор приводится к диагональному виду, а собственными векторами будут в этом случае, например, многочлены: r₀ = 1, r₁ = x-b,…, r_n = xⁿ-bⁿ.

Наконец, при a = 1 спектр j имеет вид 1^[n+1], а ранг матрицы (A-E) равен n при b ¹ 0, так что g(1) = (n+1)-rk(A-E) = 1 ¹ a(1). Мы видим, что в этом случае приведение к диагональному виду невозможно при n>0. Это означает отсутствие среди многочленов положительной степени периодических функций. В оставшемся случае a = 1, b = 0 оператор j - тождественный и его матрица будет диагональной в любом базисе.