Лекции по АиГ / Alg_15

Евклидовы пространства.

Скалярное пролизведение и его простейшие свойства.

Пусть основное поле k совпадает либо с полем R действительных, либо с полем C комплексных чисел. В дальнейшем все наши определения и результаты будут, как правило, формулироваться для случая k = C, а поле R будет рассматриваться как подполе C.

Пусть V_k векторное пространство. Функция f(u, v) = u×v, зависящая от 2 векторов этого пространства, и принимающая значения в поле k называется скалярным произведением векторов u и v, если она удовлетворяет следующим условиям (аксиомам скалярного произведения):

1. Симметричность. .

2. Первое свойство линейности.

3. Второе свойство линейности.

4. Положительность. .

Поясним, что как следует из аксиомы 1, u×uÎR и потому можно говорить о знаке этого числа.

Пространство V_k, в котором задано скалярное произведение, называется евклидовым. Очевидно, что любое подпространство евклидова пространства само будет евклидовым.

Отметим некоторые следствия из аксиом скалярного произведения. Во-первых, из аксиомы 2 вытекает, что "(uÎV) 0×u = 0. Во-вторых, используя аксиому 1, можно вывести свойства линейности по второму аргументу: и .

Примеры евклидовых пространств.

1. Пространства геометрических векторов относительно “геометрического” скалярного произведения (произведение длин на косинус угла) являются, разумеется, примерами действительных евклидовых пространств.

2. В координатном пространстве kⁿ можно определить стандартное скалярное произведение формулой: u×v = . Все аксиомы, очевидно, выполняются.

3. В пространстве матриц Mat_m´n(k) определим скалярное произведение следующим образом: A×B = , где tr(P) означает след, то есть сумму диагональных элементов квадратной матрицы P. Эта формула в более подробной записи имеет вид: 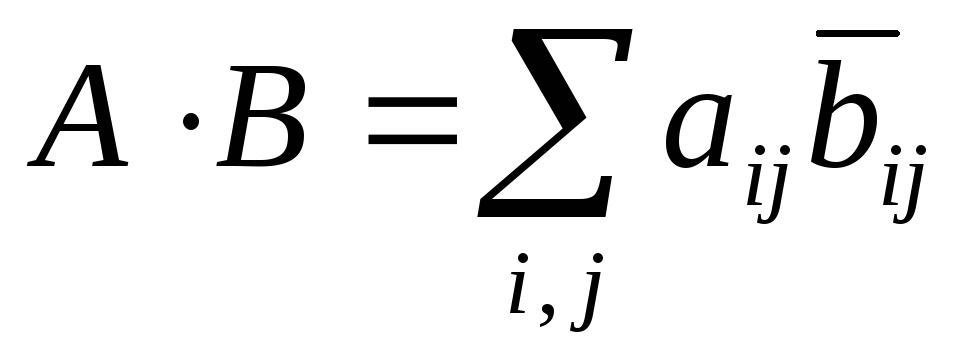. Поэтому, если обычным образом отождествить пространство Mat_m´n(k) с координатным пространством k^mn, то скалярное произведение в нашем примере оказывается таким же, как в примере 2, то есть стандартным.

4. В пространстве C[a, b] непрерывных на отрезке функций с комплексными значениями определим скалярное произведение по формуле: f×g = . Свойства линейности скалярного произведения вытекают из линейности интеграла, а свойство положительности из следующей теоремы из курса анализа: “Если интеграл по некоторому отрезку от неотрицательной непрерывной функции равен 0, то эта функция равна 0 во всех точках отрезка”. Рассматривая пространство многочленов k[x] как подпространство C[a, b], причем отрезок можно выбирать произвольно, получаем евклидово пространство многочленов.

Длина вектора.

Длиной вектора v в евклидовом пространстве V называется число |v| = . Из аксиомы 4 следует, что |v| = 0 Û v = 0. Отметим также, что |lv| = |l| |v|.

Неравенство Коши-Буняковского и неравенство треугольника.

Теорема (неравенство Коши-Буняковского).

Для любых векторов u и v евклидова пространства имеет место неравенство:

|u×v|£|u||v|, причем равенство достигается тогда и только тогда, когда векторы u и v линейно зависимы.

Доказательство.

Если левая часть неравенства обращается в 0, то утверждение очевидно. Пусть u×v = re^Ij, где r>0. Рассмотрим функцию f(t) = |u-te^Ijv|². Имеем: f(t) = (u-te^Ijv)×(u-te^Ijv) = |u|²--te^-Iju×v+t²|v|² = |u|²-2tr+ t²|v|². Мы видим, что квадратный трехчлен f(t) неотрицателен при всех значениях t. Следовательно, его дискриминант 4r²-4|u|²|v|²£0. Отсюда r£|u||v|, что и надо было установить. Если неравенство превращается в равенство, то дискриминант равен 0 и потому существует t₀, для которого f(t₀) = 0. Это означает, что u-t₀e^Ijv = 0, то есть u = lv, где l = t₀e^Ij, что и требовалось доказать.

Теорема (неравенство треугольника).

Для любых векторов u и v евклидова пространства имеет место неравенство:

|u+v|£|u|+|v|, причем равенство достигается тогда и только тогда, когда, либо один из векторов – нулевой, либо они сонаправлены, то есть u = lv, где l - положительное действительное число.

Доказательство.

Возведя обе части неравенства треугольника в квадрат, мы можем записать его в форме: (u+v)×(u+v)£|u|²+2|u||v|+|v|² или u×v+v×u£2|u||v|. Поскольку числа u×v и v×u комплексно сопряжены, доказываемое неравенство принимает вид:

Re(u×v)£|u||v|. В таком виде оно следует из неравенства Коши-Буняковского:

Re(u×v)£|Re(u×v)|£|u×v|£|u||v|. Если неравенство треугольника превращается в равенство, то и все 3 неравенства в последней строке также должны быть равенствами. Следовательно, считая, что u, v – ненулевые векторы, получаем, во-первых, u = lv (из последнего неравенства). Во-вторых, из предпоследнего неравенства следует, что |l| = |Rel|, откуда lÎR. Наконец, из первого неравенства вытекает, что l>0, что и требовалось доказать.

Угол между векторами. Ортогональность.

Пусть u и v – ненулевые векторы вещественного евклидова пространства. Из неравенства Коши-Буняковского следует, что действительное число лежит в промежутке [-1;1]. Определим угол между векторами формулой: a = . Таким образом, угол между векторами лежит в промежутке [0;p], a = 0 Û векторы сонаправлены и a = p Û векторы противонаправлены.

Если u×v = 0, то векторы называются ортогональными (u ^ v), причем это определение применяется и к случаю, когда один или оба вектора нулевые, и к случаю векторов комплексного евклидова пространства. Ясно, что в вещественном случае ортогональность ненулевых векторов означает, что угол между ними равен p/2.

Матрица Грама системы векторов; выражение скалярного произведения через координаты перемножаемых векторов.

Пусть в евклидовом пространстве V_k задана система векторов H = (h₁, h₂, …, h_m). Построим квадратную матрицу G(H) порядка m с элементами g_ij = h_i×h_j. Она называется матрицей Грама системы S. Можно записать G(H) = H^t×H. Из свойства симметрии скалярного произведения вытекает, что . Следовательно, определитель матрицы Грама всегда является действительным числом.

Если от системы H мы переходим к системе H^/ = HS, то G(H^/) = (HS)^t×(HS) = (S^tH^t)×(HS) = . В частности, если системы H и H^/ состоят из одинакового числа векторов, так что матрица S – квадратная, то detG(H^/) = |detS|²detG(H).

Допустим теперь, что V_k – конечномерно и e = (e₁, e₂, …, e_n) – базис этого пространства. Если , а , то по свойству линейности скалярного произведения имеем: , где g_ij – элементы матрицы Грама G(e). Это можно записать в форме: .

Ортогональные и нормированные системы векторов.

Определение.

Система векторов H = (h₁, h₂, …, h_m) евклидова пространства называется ортогональной, если "(i ¹ j) векторы h_i и h_j ортогональны.

Система H называется нормированной, если "i |h_i| = 1. Система, удовлетворяющая обоим условиям одновременно, называется ортонормированной.

Если система является базисом, то говорят соответственно об ортогональном, нормированном и ортонормированном базисе.

Теорема.

Ортогональная система линейно зависима тогда и только тогда, когда она содержит нулевой вектор.

Доказательство.

Пусть система H ортогональна и a₁h₁+…+a_mh_m = 0. Докажем, что если система не содержит нулевых векторов, то a_j = 0 для всех j. Умножим обе части равенства скалярно на вектор h_j. Получаем: a₁(h₁×h_j)+…+a_m(h_m×h_j) = 0. Учитывая ортогональность системы, получаем: a_j|h_j|² = 0. Поскольку h_j ¹ 0, получаем a_j = 0, что и требовалось.

Следствие.

Ортонормированная система линейно независима.

Процесс ортогонализации.

Процедура, которая сейчас будет описана, позволяет сопоставить каждой системе H = (h₁, h₂, …, h_m) векторов евклидова пространства новую систему

P = (p₁, p₂, …, p_m) векторов этого же пространства, которая будет ортогональной. Системы H и P связаны между собой рядом условий, которые перечислены в формулировке теоремы.

Теорема.

Пусть в евклидовом пространстве V задана любая система векторов H = (h₁, h₂, …, h_m). Существует ортогональная система P = (p₁, p₂, …, p_m), удовлетворяющая условиям:

, для всех i = 1,2, , m. (*)

Эти условия определяют систему P однозначно. Кроме того, имеют место следующие утверждения:

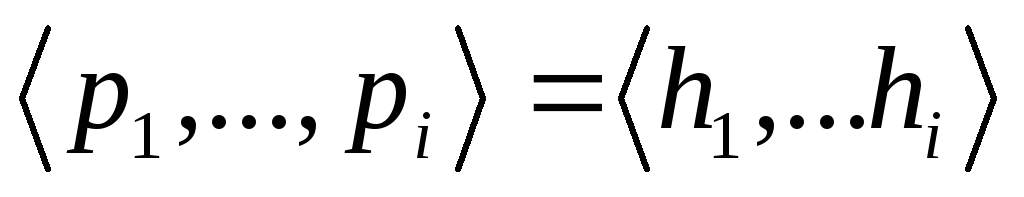1. , i = 1,2, , m.

2. Cистема H линейно независима тогда и только тогда, когда система P не содержит нулевых векторов.

3. Матрицы Грама систем H и P имеют одинаковые определители.

Доказательство.

Проведем индукцию по m. Если m = 1, то из условия (*) при i = 1 следует:

p₁-h₁ Î = {0}, откуда p₁ = h₁ определено однозначно. (Напомним, что линейная оболочка пустого множества векторов по определению совпадает с нулевым вектором 0.) Условия 1, 2, 3 очевидно удовлетворяются.

Пусть для систем, содержащих (m-1) векторов, утверждение уже доказано и, как и в формулировке теоремы, система H содержит m векторов.

Положим H^/ = (h₁, …, h_m-1). По предположению индукции однозначно определена система P^/ = (p₁, …, p_m-1), удовлетворяющая условиям 1, 2, 3. Остается построить вектор p_m и проверить для новой системы справедливость утверждений теоремы. Поскольку по предположению индукции , условие (*) для i = m можно записать в форме . Коэффициенты a_j следует подобрать так, чтобы выполнялись условия ортогональности p_m ^ p_i при i = 1, 2, …, m-1. Отсюда:

0 = p_m×p_i = h_m×p_i + a_i(p_i×p_i). Если p_i ¹ 0, то коэффициент a_i определяется однозначно: . Если же p_i = 0, то этот коэффициент может быть любым числом, что не отражается на величине вектора p_m, поскольку соответствующее слагаемое в выражении для него будет равно 0. Итак, система P = (P^/, p_m) однозначно строится по системе H. Проверим теперь для нее выполнение условий 1, 2, 3.

Поскольку , h_mÎ, а потому и Ì. С другой стороны, откуда следует обратное включение. Следовательно, эти линейные оболочки совпадают, что и утверждалось в пункте 1.

Докажем теперь утверждение 2. Линейная независимость системы H равносильна равенству dim<H> = m. Но, по уже доказанному утверждению2, <H> = <P> и потому условие принимает вид dim<P> = m, что равносильно независимости системы P. Остается заметить, что ортогональная система P линейно независима в точности тогда, когда она не содержит нулевых векторов.

Для вывода утверждения 3 заметим, что переход от системы H к системе P происходит по формулам: и потому матрица перехода S является верхней треугольной с единицами на диагонали. Поэтому detS = 1 и, следовательно, detG(P) = |detS|²detG(H) = detG(H), что и утверждалось.

Следствие 1.

Определитель Грама любой системы векторов неотрицателен; он равен 0 тогда и только тогда, когда система линейно зависима.

В самом деле, применяя к заданной системе H процесс ортогонализации, получаем ортогональную систему P с тем же определителем Грама. Однако, ввиду условия ортогональности P, G(P) = diag(|p₁|²,…|p_m|²), откуда и вытекает следствие.

Замечание.

Если система H состоит из 2 векторов u и v, то и потому detG(H) = |u|²|v|²-|u×v|². Следовательно, в этом частном случае неравенство detG(H)³0 равносильно неравенству Коши-Буняковского, которое таким образом получает новое доказательство.

Следствие 2

В любом конечномерном евклидовом пространстве V существует ортонормированный базис.

Применяя процесс ортогонализации к любому базису пространства V, получаем ортогональный базис p₁, …, p_n. Положим теперь

e_i = p_i/|p_i|. Тогда векторы e₁,…, e_n составляют ортонормированный базис V.