Линейные операторы (продолжение)

Подобие квадратных матриц.

Напомним, что две квадратные матрицы A,BÎMat_n´n(k) называются подобными над k, если существует невырожденная матрица S с элементами из k, такая, что B = S^-1AS. Подобные матрицы можно рассматривать как матрицы одного и того же оператора в разных базисах. Будем считать, что kÌC.

Теорема.

Для подобия матриц A и B порядка n необходимо, чтобы:

1. их характеристические многочлены P_A(x) и P_B(x) совпадали.

2. для всякого (комплексного) корня l их общего характеристического многочлена выполнялось условие: rk(A-lE) = rk(B-lE).

Если условие 2) заменить на условие

2а. rk(A-lE) = rk(B-lE) = n-a(l), где а(l) – алгебраическая кратность этого корня, то условия 1) и 2а) будут достаточны для подобия матриц A и B.

Если характеристические многочлены P_A(x) и P_B(x) не имеют кратных корней, то условие 1) необходимо и достаточно для подобия матриц A и B.

Доказательство.

Необходимость условия 1) уже отмечалась: характеристический многочлен матрицы оператора не зависит от выбора базиса. Легко устанавливается и необходимость условия 2). Из подобия матриц A и B следует подобие (A-lE) и (B-lE), а потому и их эквивалентность. Значит, их ранги совпадают.

Докажем теперь достаточность условий 1) и 2а). Рассмотрим в начале случай k = C Пусть j: Сⁿ® Сⁿ линейный оператор, действующий по формуле j(x) = Ax. Если e – стандартный базис Сⁿ, то A_e(j) = A. Проверим, что j приводится к диагональному виду. Поскольку мы считаем, что k = C, все корни P_A(x) лежат в k. Если l один из этих корней, то его геометрическая кратность g(l) = dim U_l. Вектор xÎU_l тогда и только тогда, когда (A-lE)x = 0, так что U_l совпадает с пространством решений однородной системы с матрицей (A-lE) и его размерность, поэтому, равна n –rk(A-lE). По условию 2а) n –rk(A-lE) = a(l). Значит, g(l) = a(l) и по теореме о диагональном виде оператора j приводится к диагональной форме. Такой же вывод можно сделать из предположения, что P_A(x) не имеет кратных корней. Итак, существует такая квадратная матрица P, что P^-1AP = diag(l₁,…, l_n), где l₁,…, l_n – набор корней характеристического многочлена P_A(x), причем каждый корень повторяется столько раз, какова его кратность. Аналогичные рассуждения доказывают существование такой невырожденной матрицы Q, что Q^-1BQ = diag(l₁,…, l_n), причем с тем же набором диагональных элементов, поскольку P_A(x) = P_B(x). Итак, матрицы A и B подобны одной и той же диагональной матрице, а, следовательно, подобны и между собой. (Легко видеть, что в качестве преобразующей матрицы S в равенстве B = S^-1AS можно взять S = PQ^-1.)

В случае kÌC можно воспользоваться следующей леммой.

Лемма.

Пусть матрицы A и B подобны над полем C, а их элементы лежат в некотором меньшем поле k. Тогда преобразующую матрицу S можно выбрать таким образом, чтобы все ее элементы также лежали в поле k.

Доказательство.

Равенство B = S^-1AS равносильно равенству SB = AS. Найдем все матрицы X, удовлетворяющие условию XB = AX. Это равенство можно рассматривать как систему из n² однородных линейных уравнений с n² неизвестными элементами матрицы X. Пусть S₁,…, S_k – стандартная ФСР этой системы. Как мы отмечали, элементы всех этих матриц лежат в поле k. Преобразующая матрица S является их линейной комбинацией: S = l₁S₁+…+l_kS_k. Покажем, что в этом равенстве каждый коэффициент l_mÎC можно заменить на m_mÎk, не меняя при этом остальных коэффициентов и сохраняя невырожденность матрицы S. Положим S(x) = xS_m+. Тогда, очевидно, r(x) = det S(x) представляет собой многочлен от x, который не равен 0 тождественно, поскольку r(l_m) = det S ¹ 0. Степень этого многочлена не выше n, так что он имеет не более n корней. Поэтому в бесконечном множестве k можно выбрать такой элемент m_m, что r(m_m) ¹ 0. Лемма доказана.

Примеры.

1. Матрицы и имеют разные характеристические многочлены: P_A(x) = x²-7x+1 и P_B(x) = x²-7x+7 и потому не подобны.

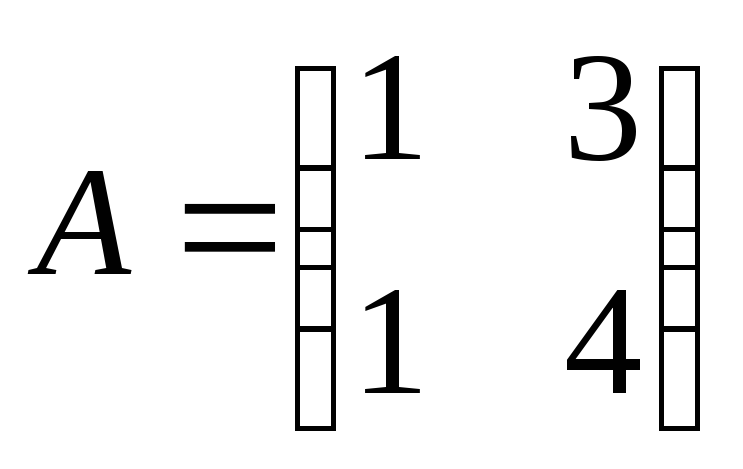2. Матрицы и имеют одинаковые характеристические многочлены P_A(x) = P_B(x) = x²-5x+1. Поскольку этот многочлен не имеет кратных корней, матрицы подобны. Элементы преобразующей матрицы S удобнее всего искать, рещая систему уравнений AS = SB. Оказывается, что элементы последней строки S – свободные неизвестные, а элементы ее первой строки – главные неизвестные. Стандартная ФСР имеет вид: . Обе матрицы невырожденны и потому каждая из них может быть выбрана в качестве преобразующей.

3. Для матриц и характеристические многочлены совпадают: P_A(x) = P_B(x) = -(x-1)³. Однако, rk(A-E) = 2, rk(B-E) = 1 и потому матрицы не подобны.

4. Матрицы и имеют равные характеристические многочлены:P_A(x) = P_B(x) = -(x-1)²(x-2). Кроме того, rk(A-E) = rk(B-E) = 1 = 3-a(1). Следовательно, матрицы A и B подобны. Обе матрицы имеют собственный вектор, относящийся к собственному значению 2 и два независимых собственных вектора, относящихся к значению 1. Из этих векторов-столбцов составляем матрицы P и Q, преобразующие A и B в диагональную матрицу diag(2,1,1). При этом можно взять ; . Матрица S, преобразующая A в B равна S= PQ^-1 = .

5. Матрицы и имеют равные характеристические многочлены: P_A(x) = P_B(x) = x⁴. Кроме того, rk A = rk B = 2, но это число не совпадает с числом 4-a(0) = 0. Поэтому сформулированные выше условия оставляют открытым вопрос о подобии этих матриц. В действительности эти матрицы не являются подобными. Можно проверить, что A² ¹ 0, но B² = 0, что невозможно для подобных матриц.