
- •Раздел 7 181
- •Раздел 7
- •§7.1. Определение линейного пространства
- •§7.2. Линейная зависимость, размерность и базис в линейном пространстве
- •§7.3. Подмножества линейного пространства
- •§7.4. Операции с элементами линейного пространства в координатном представлении
- •§7.5. Изоморфизм линейных пространств
§7.4. Операции с элементами линейного пространства в координатном представлении
|
Определение 7.4.1. |
Коэффициенты
|
Заметим,
что в силу теоремы 7.2.1. элемент
![]() линейного пространства
линейного пространства
![]() в
базисе
в
базисе
![]() однозначно представляетсяn-компонентным
столбцом, называемым «координатным
представлением элемента
однозначно представляетсяn-компонентным
столбцом, называемым «координатным
представлением элемента
![]() в базисе
в базисе![]() »,
», .
.
В
![]() базис может быть выбран не единственным
способом и потому необходимо установить
правило изменения координат элемента
линейного пространства
базис может быть выбран не единственным
способом и потому необходимо установить
правило изменения координат элемента
линейного пространства
![]() при переходе от одного базиса к другому.
при переходе от одного базиса к другому.
Пусть
в
![]() даны два базиса: “старый”
даны два базиса: “старый”
![]() и “новый”
и “новый”![]() ,
с соответствующими координатными
разложениями элементаx:
,
с соответствующими координатными
разложениями элементаx:
![]() и
и![]() .
Пусть, кроме того, известны разложения
элементов “нового” базиса по элементам
“старого”
.
Пусть, кроме того, известны разложения
элементов “нового” базиса по элементам
“старого”![]() .
.
|
Определение 7.4.2. |
Матрица
|
Отметим, что это определение является обобщением определения 1.8.2. Тогда справедлива
|
Теорема 7.4.1.
|
Координаты
|
|
|
Доказательство:
Пусть
известно разложение элементов “нового”
базиса по “старому”
или
Теорема доказана. |
Иначе
говоря, если столбец элементов “нового”
базиса выражаются через столбец элементов
“старого” при помощи умножения слева
на транспонированную матрицу перехода
![]() ,
то координатный столбец в “старом”
базисе равен произведению матрицы
перехода на координатный столбец в
“новом” базисе. В матричной форме: если
,
то координатный столбец в “старом”
базисе равен произведению матрицы
перехода на координатный столбец в
“новом” базисе. В матричной форме: если ,
то
,
то![]() .
.
Рассмотрим
теперь вопрос о том, как операции с
элементами линейного пространства
выполняются в координатной форме. Пусть
в конкретном базисе
![]() и
и![]() ,
тогда в силу определения базиса и аксиом
линейного пространства будут справедливы
следующие соотношения.
,
тогда в силу определения базиса и аксиом
линейного пространства будут справедливы
следующие соотношения.
1.
Для
операции сравнения:
два элемента в
![]() равны тогда и только тогда, когда
равны тогда и только тогда, когда
![]() ,
или в координатной форме
,
или в координатной форме
 .
.
2. Для операции сложения:
![]() ,
или в координатной форме
,
или в координатной форме
![]() .
.
3. Для операции умножения на число:
![]() ,
или в координатной форме
,
или в координатной форме
![]() .
.
Откуда следует, что элементы конечномерного линейного пространства не только могут представляться матрицами (столбцами), но и правила выполнения операций с этими элементами совпадают с определением соответствующих матричных операций.
Отметим,
наконец, что факт равенства или неравенства
двух элементов в координатной форме
можно проверять в любом базисе, поскольку
в силу невырожденности
![]() будут справедливы соотношения
будут справедливы соотношения![]()
§7.5. Изоморфизм линейных пространств
Рассмотрим
два линейных пространства: множество
многочленов
![]() степени не выше, чем 2 , и множество
векторов трехмерного геометрического
пространства.
степени не выше, чем 2 , и множество
векторов трехмерного геометрического
пространства.
Операции сложения многочленов и их умножения на число выглядят следующим образом:

Аналогичные операции с трехмерными векторами в координатной форме, в свою очередь, записываются так:
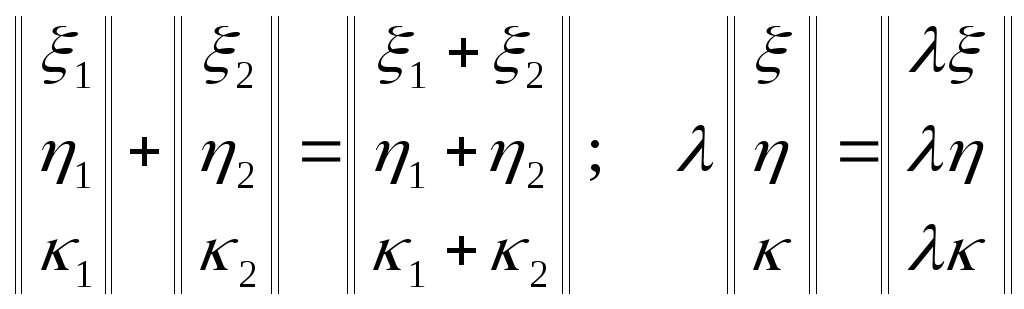 .
.
Сопоставляя эти записи, можно заметить, что природа данных множеств не играет роли, когда исследуются их характеристики, связанные только с операциями сравнения, сложения и умножения на число.
Отмеченное свойство линейных пространств носит название изоморфизма. Более точно его описывает
|
Определение 7.5.1. |
Два
линейных пространства
|
|
|
1.
2.
Отображение
|
Напомним,
что отображение
![]() являетсявзаимно
однозначным (биективность
являетсявзаимно
однозначным (биективность
![]() ),
если:
),
если:
а)
разные элементы из
![]() имеют в
имеют в![]() разные образы (инъективность
разные образы (инъективность
![]() );
);
б)
каждый элемент из
![]() является образом некоторого элемента
из
является образом некоторого элемента
из![]() (сюръективность
(сюръективность
![]() ).
).
|
Теорема 7.5.1. (об изоморфизме) |
Два
линейных конечномерных пространства
|
|
|
Доказательство:
Пусть
Допустим,
что
Случай n < m рассматривается аналогично.
Теорема доказана. |
|
Теорема 7.5.2. |
Число
линейно независимых элементов в любом
конечном наборе элементов из
|
|
|
Доказательство:
Следует
из изоморфности линейного пространства
|
|
Следствие 7.5.1. |
k
элементов в
|
|
Следствие 7.5.2. |
Матрица
перехода невырожденная, то есть
|
|
|
Доказательство:
Предположим
противное,
Следствие доказано. |
|
Следствие 7.5.3. |
Существует
матрица
|
Для
обратной матрицы перехода справедливы
соотношения
 и
и![]() ,
вытекающие из равенств
,
вытекающие из равенств ,
,![]() и теоремы 7.4.1.
и теоремы 7.4.1.
|
Следствие 7.5.4. |
Пусть
в
|
|
|
Доказательство:
Следует
из того, что данное подпространство
|
|
|
линейных
уравнений
|
|
Следствие 7.5.5. |
Пусть
в
|
|
|
Доказательство:
Аналогично рассуждениям, приведенным для следствия 7.5.4. |
|
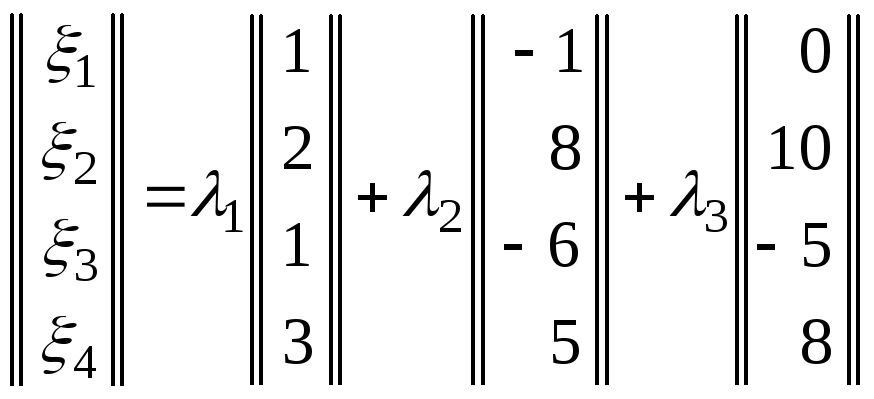
Задача 7.5.1. |
Проверить,
что элементы
|
|
Решение: |
1.
Для того, чтобы из элементов
|
|
|
2.
Обозначим искомые координаты элемента
x
через
3. Использовав условие равенства двух элементов в координатной форме, получим систему линейных уравнений
решив
которую по правилу Крамера (теорема
6.4.1.) или методом Гаусса (§6.8.), получим
|
|
Задача 7.5.2. |
Найти
матрицу перехода от базиса в
|
|
Решение: |
1.
Пусть
|
|
|
где
матрицы
Обозначим
через
Тогда
2. Подсчитав произведение
используя,
например, схему описанную в §6.8. для
выражений вида
|
|
Задача 7.5.3. |
В линейном пространстве многочленов степени не выше чем 3, найти базис и размерность пересечения двух линейных оболочек элементов
|
|
Решение: |
1.
По теореме 7.4.1. каждая из линейных
оболочек является подпространством.
Первое из них
Пусть каждое из уравнений этих систем имеет вид
Тогда,
воспользовавшись изоморфизмом между
где
которое
будет выполняться при любых
Решив эту систему, например, по схеме описанной в §6.8., получим общее решение в виде |
|
|
откуда
заключаем, что существует два независимых
набора искомых чисел
Аналогично
строим однородную систему линейных
уравнений, задающую
Наконец,
подпространство
общее решение которой есть
и,
следовательно, для
|
1)
То есть имеется возможность устанавливать
факт «равенства
![]() и
и
![]() »
»![]() или «неравенства
или «неравенства![]() и
и![]() »
»![]() для любых двух элементов
для любых двух элементов![]() .
.
1) Предполагается, что операции сложения и умножения на число выполняются в соответствии с ранее данными определениями.
1) То
есть для любого натурального n
в данном линейном пространстве найдется
n+1
линейно независимый элемент, например,
система функций вида
![]() .
.

 ,
,
 ,
,
 и
и
 .
. ,
которое имеет место, поскольку
,
которое имеет место, поскольку .
. .
.
 .
.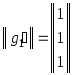 ,
,
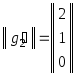 ,
,
 ,
, ,
,
 и
и
 .
.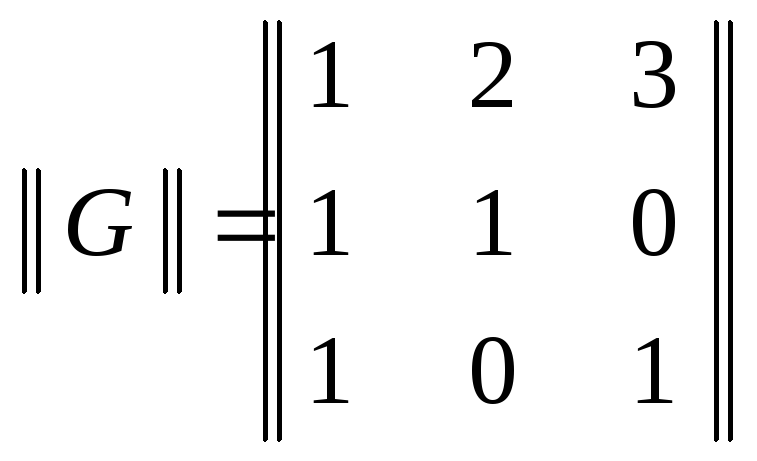 и
и
 .
.

 .
. и
и

 .
. ,
, ,
,
 ,
,


 ,
, .
.