
§Пр.4.3. Операции с тензорами
Вводимые ниже операции с тензорами во всех случаях требуют обоснования того, что результатом каждой из них является также тензор. В рамках данного курса эти утверждения предлагаются в качестве упражнений.
Сложение тензоров
|
Определение Пр.4.3.1. |
Пусть
даны два тензора типа
|
|
Пример 4.3.1. |
Сумма
двух линейных операторов
|
Умножение тензоров на число
|
Определение Пр.4.3.2. |
Пусть
дан тензор типа
|
|
Замечание: |
нетрудно
показать, что множество тензоров типа
|
Тензорное произведение
|
Определение Пр.4.3.3. |
Пусть
даны два тензора типа
Иногда тензорное произведение обозначают символом . |
|
Пример Пр.4.3.2. |
Мы
видели, что элементы линейного
пространства
|
|
|
Заметим,
|
|
Задача Пр.4.3.1. |
Определить
тип и матрицу тензора
|
|
Решение |
По
определению тензорного произведения,
c
есть тензор типа
Таким образом матрица тензора c имеет вид:
|
Свертывание тензоров
|
Определение Пр.4.3.4. |
Пусть
дан тензор типа
|
Заметим,
что в последнем равенстве правая часть
- это сумма n
слагаемых, где m
- индекс, по которому выполняется
суммирование, а само данное тензорное
равенство равносильно
![]() скалярным равенствам.
скалярным равенствам.
|
Пример Пр.4.3.3. |
Свертка
тензора типа
|
Операция
свертки часто комбинируется с операцией
умножения тензоров. Например, результатом
произведения один раз ковариантного
тензора на один раз контравариантный
с последующей сверткой является
инвариант, представляющий значение
линейного функционала в
![]() .
Действительно,
.
Действительно,
![]() .
В этом случае говорят, что тензор
.
В этом случае говорят, что тензор
![]() свертывается
с тензором
свертывается
с тензором
![]() .
.
|
Задача Пр.4.3.2. |
Даны тензоры:
a
-
типа
b
-
типа
c
-
типа
Найти
свертки
|
|
Решение |
1.
По определению операции свертывания,
2.
Аналогично
|
Транспонирование тензоров
Как уже отмечалось ранее, перестановка местами любой пары ковариантных (или пары контравариантных) индексов у тензора, то есть транспонирования тензора, вообще говоря, приводит к его изменению, поскольку в определении тензора говорится об упорядоченной системе индексов. При этом новый тензор будет того же типа, что и исходный.
В общем случае для группы, состоящей из N верхних (или нижних) индексов, существует N! различных способов перестановок. Это означает, что, переставляя данные индексы, можно построить N! новых тензоров.
|
Задача Пр.4.3.3. |
Тензор
|
|
Решение |
Данный
тензор можно транспонировать по паре
контравариантных индексов i
и j.
После перестановки соответствующих
элементов получаем тензор с матрицей
|
Симметрирование и альтернирование тензоров
|
Определение Пр.4.3.5. |
Тензор называется симметричным относительно группы (верхих или нижних) индексов, если он не меняется при перестановке любых двух индексов, принадлежащих данной группе. |
|
Определение Пр.4.3.6. |
Тензор называется антисимметричным (или кососимметричным) относительно группы индексов, если он меняет, в смысле указанного выше определения равенства тензоров, свой знак на противоположный при перестановке любых двух индексов, принадлежащих данной группе. |
Выделим у тензора группу, состоящую из N индексов (либо верхних, либо нижних), построим путем перестановок индексов данной группы N! всевозможных новых тензоров и возьмем их среднее арифметическое. В результате мы получим тензор, симметричный по выбранной группе индексов.
Данная операция называется симметрированием тензора по группе индексов. Группа индексов, по которой выполняется симметрирование тензора, выделяется круглыми скобками.
|
Пример Пр.4.3.4. |
N=1 |
|
|
|
N=2 |
|
|
|
N=3 |
|
|
|
... |
... |
Операция симметрирования часто комбинируется с умножением, причем имеет место следующий порядок действий: сначала умножение, а потом симметрирование.
|
Пример Пр.4.3.5. |
|
Выделим
у тензора группу, состоящую из N
индексов (либо верхних, либо нижних),
построим путем перестановок индексов
данной группы N!
всевозможных новых тензоров, приписав
каждому из них знак
![]() ,
где
,
где
![]() - число беспорядков в перестановке чисел
- число беспорядков в перестановке чисел
![]() ,
и возьмем их среднее арифметическое. В
результате мы получим тензор,
антисимметричный по выбранной группе
индексов.
,
и возьмем их среднее арифметическое. В
результате мы получим тензор,
антисимметричный по выбранной группе
индексов.
Данная операция называется альтернированием тензора по группе индексов. Группа индексов, по которой выполняется альтернирование тензора, выделяется квадратными скобками.
|
Пример Пр.4.3.6.
|
N=1 |
|
|
|
N=2 |
|
|
|
N=3 |
|
|
|
... |
... |
Операция альтернирования часто комбинируется с умножением, причем имеет место следующий порядок действий: сначала умножение, а потом альтернирование.
|
Пример Пр.4.3.7. |
|
Заметим, что как симметрирование кососимметричного тензора, так и альтернирование симметричного дает нулевой тензор.
|
Задача Пр.4.3.4. |
Тензор
|
|
Решение |
1.
Тензор
Тензор
2.
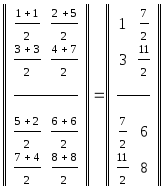
Тогда тензор
тензор
|
|
|
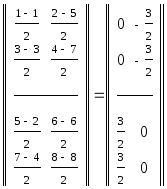
а
тензор
|

 .
.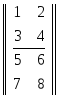 ,
и b
-
тензор типа
,
и b
-
тензор типа
 .
. ;
; ;
;
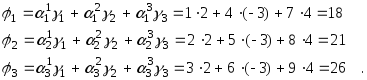
 .
Найти матрицу транспонированного
тензора.
.
Найти матрицу транспонированного
тензора. .
.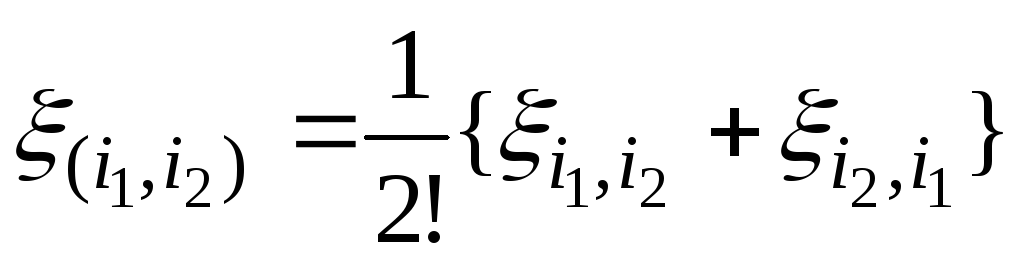



 .
Найти матрицы тензоров
.
Найти матрицы тензоров
 (См. задачу Пр.4.3.3.)
(См. задачу Пр.4.3.3.) ,
в которой элементы первых столбцов
блочных матриц исходного тензора
записаны в первой блочной строке, а
элементы вторых столбцов блочных
матриц исходного тензора записаны во
второй блочной строке.
,
в которой элементы первых столбцов
блочных матриц исходного тензора
записаны в первой блочной строке, а
элементы вторых столбцов блочных
матриц исходного тензора записаны во
второй блочной строке.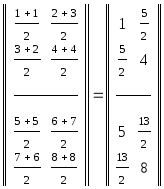 ,
, ,
, .
.