Приложение 4 100

Элементы тензорного исчисления

Приложение 4

ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ

§Пр.4.1. Замечания об определении объектов в линейном пространстве

В предыдущих разделах курса линейной алгебры исследовались наиболее часто встречающиеся в приложениях виды объектов в линейном пространстве, такие как: элемент линейного пространства, линейный функционал, линейный оператор, билинейный функционал и т.д., хотя вполне очевидно, что в линейном пространстве могут быть определены и иные, быть может, более сложные объекты, представляющие практический интерес.

Определение всех рассмотренных ранее объектов давалось вне зависимости от наличия или отсутствия базиса линейного пространства, причем в случае существования базиса для каждого из объектов приводился альтернативный, покомпонентный способ его описания. И поскольку замена базиса меняет, вообще говоря, данное описание, то специально исследовался вопрос о характере этого изменения.

Однако естественно допустить, что в линейном пространстве существуют объекты, которые можно определить, используя лишь значения их компонентов в некотором базисе. Такой подход привлекателен тем, что:

во-первых, в этом случае не требуется объяснять, что представляет собой данный объект безотносительно к базису,

и, во-вторых, определения объектов разной природы могут быть выполнены единообразно.

С другой стороны, недостатком такой схемы является очевидная зависимость описания объекта от выбора базиса, то есть необходимость указывать (в самом определении объекта!), что происходит с его компонентами при переходе от одного базиса к другому.

Для оценки целесообразности использования определения объектов в через их компоненты приведем в таблице Пр.4.1.1. основные, рассмотренные нами ранее, типы объектов, формы их представления в базисе и правила изменения этого представления при переходе от базиса к базису .

Тип объекта в	Координатное представление в базисе	Правило изменения координатного представления при переходе к базису
Элемент x	Столбец	или
Линейный функционал	Строка , где	или
Линейный оператор	, где	или
Билинейный функционал	, где	или
Квадратичный функционал	, где	или

Таблица Пр.4.1.1.

Как и ранее, будем предполагать, что матрица перехода имеет компоненты , где , а матрица обратного перехода имеет компоненты , то есть .

Сопоставление формул третьей колонки таблицы позволяет заметить, что для данных объектов:

1. Значения их компонентов в базисе линейны по значениям компонентов в базисе .

2. Коэффициентами в этих формулах служат: либо компоненты матриц или , либо и той и другой одновременно.

В курсе линейной алгебры нами были рассмотрены далеко не все виды объектов, которые обладают подобными трансформационными свойствами. Например, в можно ввести произведение элементов , поставив в каждом базисе упорядоченной паре элементов и в соответствие матрицу размера , имеющую вид: .

Нетрудно убедиться, что объект при переходе от базиса к базису меняется в соответствии с правилами 1 и 2. Действительно, из и следует, что , или же, в матричном виде, . Последнее равенство означает, что введенное нами произведение элементов обладает свойствами 1 и 2.

Рассмотрим другой пример, демонстрирующий существование более сложных объектов, обладающих данными свойствами. Достаточно часто в физических приложениях используется метод, в котором линейный оператор описывает зависимость одного вектора, характеризующего некоторое свойство точки пространства, от другого вектора, являющегося иной характеристикой этой же точки.

Например, закон Гука связывает вектор силы , возникающей в результате упругой деформации, с вектором деформации соотношением:

,

или же индукция электрического поля выражается через напряженность электрического поля формулой:

.

Если среда однородная, то коэффициенты матриц этих операторов константы. Однако если исследуемые свойства среды меняются от точки к точке, то соответствующие операторы уже не будут линейными, и может возникнуть вопрос о характере их зависимости от координат.

В этом случае можно ввести в рассмотрение объект, компоненты которого являются частными производными компонентов матрицы оператора по переменным и . Для рассматриваемых примеров таких частных производных будет 27 и их удобно представить в виде трехмерной таблицы (или, как иногда говорят, “куб-матрицы”).

Например, для закона Гука этот объект состоит из трех матриц вида:

.

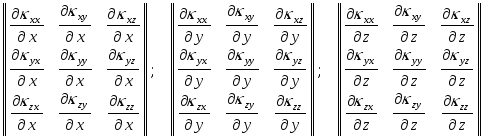В общем случае n-мерного линейного пространства можно ввести объект, называемый производной оператора, обозначаемый и задаваемый в конкретном базисе упорядоченным набором из чисел.

Выясним закон преобразования компонентов этого объекта при переходе от базиса к базису .

Поскольку правило изменения компонентов матрицы оператора в имеет вид (или ), то из правила дифференцирования сложной функции следует, что

или, в матричной форме, . Отсюда делаем заключение, что введенный нами новый объект также обладает свойствами 1 и 2.

С другой стороны, отметим, что не всякий однозначно определяемый своими компонентами объект будет обладать подобными трансформационными свойствами.

Например, рассмотрим однокомпонентный объект , значение которого для каждого элемента пространства есть сумма компонентов . Для него в базисе имеем и, хотя значение и определяется однозначно в базисе , оно не выражается линейно через , так как .

Таким образом, мы приходим к заключению, что в конечномерном линейном пространстве существует достаточно широкий класс объектов, задаваемых:

- совокупностью значений своих компонентов в некотором базисе и

- свойствами вида 1 и 2, характеризующими изменения этих компонентов при переходе от одного базиса к другому.

Объекты, обладающие перечисленными свойствами, называют тензорами, уточняя это название, в случае присутствия матриц или ^T в формулах пересчета компонентов тензора при замене базиса, определением ковариантный (то есть преобразующийся так же, как и базисные элементы), или же, в случае присутствия матриц или , определением контравариантный.

§Пр.4.2. Определение и обозначение тензоров

Общее определение тензора, исходя из вышеизложенных соображений, следовало бы предложить, например, в такой форме:

Будем говорить, что в вещественном линейном пространстве определен тензор типа , q раз контравариантный и p раз ковариантный (или -валентный), если в задан объект, который в каждом базисе характеризуется упорядоченным набором чисел (где - контравариантные индексы и - ковариантные), преобразующихся при переходе от базиса к базису по закону:

,

где ; и ; , а и есть соответственно компоненты матрицы перехода и ей обратной .

Громоздкость и неудобочитаемость стандартной схемы обозначений применительно к тензорам очевидны уже на примере этого определения. Поэтому в тензорном исчислении используется специальная, более компактная форма описания тензорных объектов и операций с ними, основу которой составляют следующие правила:

Запись тензоров

1. Упорядоченный набор вещественных чисел, являющихся компонентами тензора, образует -мерную таблицу (называемую также -мерной матрицей, или -мерным массивом), каждый элемент которой однозначно определен набором значений контравариантных индексов и ковариантных индексов .

Если какой-либо из индексов принимает значения от 1 до n, то в записи тензора перечень значений индекса не указывается и предполагается, что выписаны компоненты тензора для всех этих значений.

Пример Пр.4.2.1.

запись означает, что

2. Порядок следования индексов в записи тензоров существенен. Для того чтобы избежать возможной неоднозначности, применяется следующее правило: если необходимо выписать последовательно все компоненты тензора (например, в виде одной строки), то в первую очередь увеличиваются индексы расположенные ближе к правому концу индексного списка.

Пример Пр.4.2.2.

тензор в имеет следующий порядок компонентов: .

3. В тензорных записях для отличия контравариантных индексов от ковариантных принято первые обозначать верхними индексами, а вторые - нижними. При этом, чтобы сохранить общий порядок следования индексов в списке, в запись каждого индекса добавляется символ “точка” под каждым верхним индексом и над каждым нижним.

Пример Пр.4.2.3.

.

4. Если точки не использованы в записи тензора, то предполагается, что нижние индексы следуют в списке после верхних.

Пример Пр.4.2.4.

линейный оператор 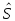, переводящий базис в базис , является двухвалентным тензором типа (1,1) (один раз контравариантным и один раз ковариантным), причем его компоненты совпадают с компонентами матрицы перехода , как следствие совпадения определения 7.3.2. и определения матрицы линейного оператора 8.3.1.

Соглашение о суммировании

Пусть имеется выражение, являющееся произведением сомножителей, имеющих как верхние, так и нижние индексы, причем некоторый индекс встречается в записи выражения дважды: один раз как верхний, а второй раз как нижний. Тогда под таким выражением понимается сумма членов данного вида, выписанных для всех значений повторяющегося индекса.

В случае присутствия в выражении нескольких пар совпадающих индексов имеет место многократное суммирование.

Пример Пр.4.2.5.

1. Квадратичный функционал записывается теперь в виде .

2. Система линейных уравнений вида с учетом соглашений о тензорных обозначениях записывается просто как .

Используя соглашения о тензорных обозначениях и принимая во внимание, что числа и (- компоненты матриц прямого и обратного перехода между базисами и ) являются также компонентами тензоров типа (1,1), сформулируем

Определение Пр.4.2.1.

Будем говорить, что в вещественном линейном пространстве определен тензор типа , q раз контравариантный и p раз ковариантный, если в задан объект, который в каждом базисе характеризуется упорядоченным набором чисел (где - контравариантные индексы и - ковариантные), изменяющиеся при переходе от базиса к базису по закону: .

Определение Пр.4.2.2.

Число называется валентностью (или рангом) тензора .

Определение Пр.4.2.3.

Два тензора называются равными, если они одного и того же типа и во всех базисах имеют равные компоненты.

Замечания: 1. Для равенства тензоров одного типа достаточно, чтобы их компоненты были равны лишь в некотором базисе, так как из формул пересчета компонентов следует, что эти тензоры будут иметь равные компоненты и в любом другом базисе.