§5.6. Понятие группы
|
Определение 5.6.1. |
Множество
G
называется группой
по
отношению к заданной операции,
если любым двум его элементам
 и и оставлен в соответствие третий элемент
этого же множества, называемыйпроизведением
и обозначаемый оставлен в соответствие третий элемент
этого же множества, называемыйпроизведением
и обозначаемый
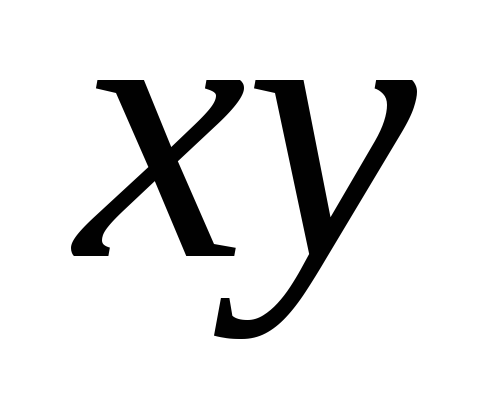 ,
и если выполняются следующие условия: ,
и если выполняются следующие условия:
1.
 ; ;
2.
существует элемент
e
такой, что для любого
 ; ;
3.
для каждого x
существует элемент
 такой, что такой, что . . |
Если,
кроме того,
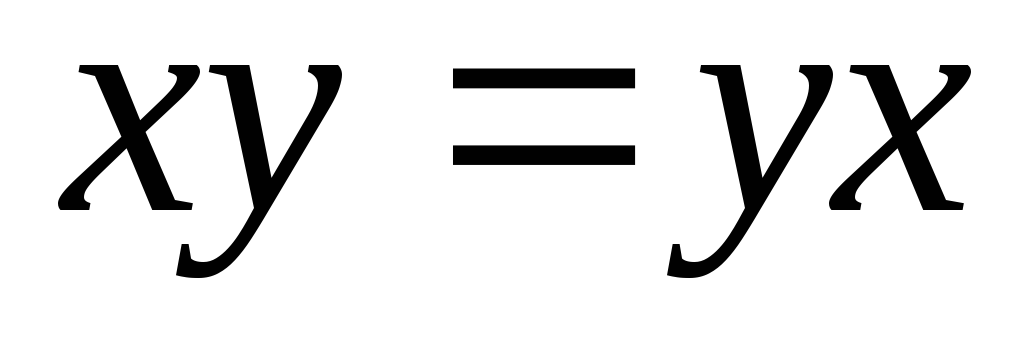
 ,
то группа называется коммутативной
или абелевой.
,
то группа называется коммутативной
или абелевой.
|
Пример 5.6.1. |
К
группам относятся, например, следующие
множества:
1)
Множество вещественных чисел
относительно операции сложения
образует группу, где e
-
число 0.
2)
Множество положительных вещественных
чисел образует группу относительно
операции умножения, где e
-
число 1.
3)
Множество поворотов плоскости вокруг
фиксированной точки образует группу
относительно операции композиции.
4)
Множество аффинных преобразований
плоскости образует группу относительно
операции композиции. |
1)
Правило
нахождения определителя квадратной
матрицы порядка
n
приводится в разделе 6.
1)
Для
 эти соотношения проверяются непосредственно
по определению 1.1.9., случай произвольногоn
рассматривается в разделе 6 .
эти соотношения проверяются непосредственно
по определению 1.1.9., случай произвольногоn
рассматривается в разделе 6 .

