
§5.3. Линейные операторы на плоскости
Пусть
на плоскости с декартовой системой
координат
![]() каждой ее точке
каждой ее точке![]() поставлена в однозначное соответствие
точка
поставлена в однозначное соответствие
точка![]() ,
то есть, согласно определению 5.2.6., задано
преобразование этой плоскости
,
то есть, согласно определению 5.2.6., задано
преобразование этой плоскости![]() .
Пусть координатные представления
радиус-векторов этих точек суть
.
Пусть координатные представления
радиус-векторов этих точек суть![]() и
и![]() ,
тогда координаты
,
тогда координаты![]() и
и![]() будут некоторыми функциями от
будут некоторыми функциями от![]() и
и![]()
 и потому равенство
и потому равенство![]() можно рассматривать как координатное
представление оператора
можно рассматривать как координатное
представление оператора![]() ,
являющегося данным преобразованием
плоскости в системе координат
,
являющегося данным преобразованием
плоскости в системе координат![]() .
.
Далее
мы будем рассматривать частные, но
важные для приложений виды функций
![]() и
и![]() .
.
|
Определение 5.3.1. |
Оператор
|
При
помощи операций с матрицами линейный
оператор может быть записан в виде
![]() ,
где матрица
,
где матрица![]() называетсяматрицей
линейного оператора
называетсяматрицей
линейного оператора
![]() ,
являющейся его координатным представлением
в
,
являющейся его координатным представлением
в![]() .
.
|
Определение 5.3.2. |
Оператор
Если
же
|
|
Пример 5.3.1. |
К линейным однородным операторам относятся:
-
оператор
- оператор ортогонального проектирования радиус-векторов точек плоскости на некоторую заданную ось, проходящую через начало координат. |
|
Теорема 5.3.1. |
Для
линейного однородного оператора
1.
2.
|
|
|
Доказательство:
В справедливости утверждения теоремы убедимся непосредственной проверкой, используя правила действия с матрицами. Например, для 1º имеем |
|
|
Теорема доказана. |
|
Теорема 5.3.2. |
Если
для некоторого оператора
1.
2.
то этот оператор линейный и однородный. |
|
|
Доказательство:
Пусть
Вводя
обозначения
И,
окончательно,
Теорема доказана. |
Отметим
также, что образом вектора
![]() с
с![]() в базисе
в базисе
![]() является вектор
является вектор
![]() с координатным представлением
с координатным представлением![]() .
.
Из теорем 5.3.1. и 5.3.2. вытекают:
|
Следствие 5.3.1. |
Столбцами
матрицы линейного однородного оператора
|
|
Следствие 5.3.2. |
Каждому линейному однородному оператору преобразования плоскости в конкретном базисе соответствует квадратная матрица второго порядка, а каждая квадратная матрица второго порядка задает в этом базисе некоторый линейный однородный оператор. |
|
Задача 5.3.1. |
Исходя из правил действия с матрицами, показать, что для линейных однородных операторов на плоскости справедливы утверждения:
1.
Матрица произведения линейных
однородных операторов равна произведению
матриц сомножителей:
2.
Если
|
Выясним теперь, как изменится матрица линейного однородного оператора при замене базиса. Имеет место
|
Теорема 5.3.3. |
Пусть
в системе координат
|
|
|
Доказательство:
Пусть
в исходной системе координат действие
задается формулой
Подставляя
два последних соотношения в первое и
принимая во внимание утверждение
теоремы 1.8.2. о невырожденности матрицы
перехода
|
|
|
Наконец,
вычитая последнее равенство почленно
из равенства
Теорема доказана. |
|
Следствие 5.3.3. |
Величина
|
|
|
Доказательство:
Поскольку
определитель произведения матриц
равен произведению определителей
сомножителей, то, в силу теоремы 5.3.3.
и невырожденности матрицы перехода
Следствие доказано. |
|
Задача 5.3.2. |
В
ортонормированной системе координат
найти матрицу оператора, ортогонально
проектирующего радиус-векторы точек
координатной плоскости на прямую
|
|
|
Пусть
точка-прообраз M
имеет радиус-вектор
Из
рис. 5.3.1. следует, что
|
y
O x
M
Рисунок 5.3.1.
|
|
|
Поскольку
нормальный вектор прямой
Используя правила операций с матрицами, получаем окончательно, что
|

 .
.
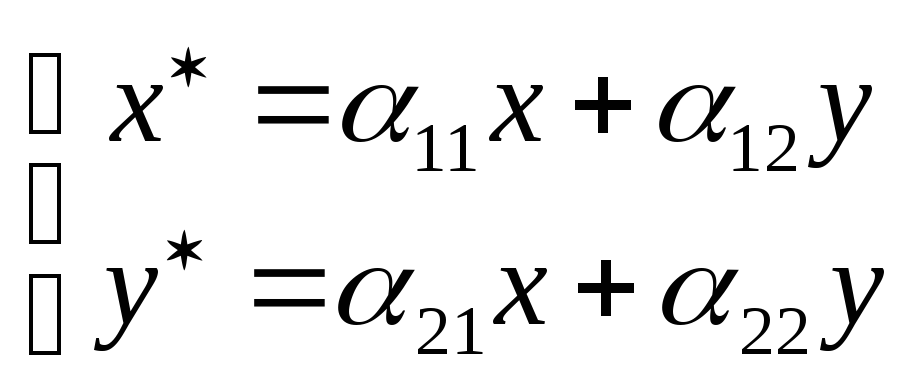 ,
или
,
или .
.



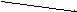
 Р
Р ешение:
ешение: или
или
 .
. ,
то есть
,
то есть
 .
.