
§3.3. Плоскость в пространстве
Пусть даны система координат
![]() в пространстве и плоскостьS ,
проходящая через точку
в пространстве и плоскостьS ,
проходящая через точку![]() с лежащими наSнеколлинеарными
векторами
с лежащими наSнеколлинеарными
векторами![]() и
и![]() .
.
|
Определение 3.3.1. |
Векторы
|
|
Теорема 3.3.1. |
Множество
радиус-векторов точек на плоскости S
представимо в виде
|
|
|
Доказательство:
Пусть
|
|
|
Откуда, в силу теоремы 1.4.3. и леммы 1.4.1., получаем
и, следовательно, уравнение плоскости будет иметь вид
где
Теорема доказана. |
S
O
Рисунок 3.3.1. |
Получим теперь координатное представление
множества радиус-векторов всех точек
плоскости
![]() .
Пусть
.
Пусть ,
, ,
, и
и ,
тогда будут справедливы следующие
теоремы.
,
тогда будут справедливы следующие
теоремы.
|
Теорема 3.3.2. |
Всякая плоскость в любой декартовой системе координат может быть задана уравнением вида
|
|
|
Доказательство:
Условие компланарности векторов
Откуда
|
|
|
а
Условие невозможности одновременного
равенства нулю чисел A,BиCвытекает из неколлинеарности векторов
Теорема доказана. |
|
Теорема 3.3.3. |
Всякое
уравнение вида
|
|
|
Доказательство:
Непосредственной проверкой убеждаемся,
что уравнение
а в случае
В обоих случаях эти уравнения определяют плоскость, проходящую через некоторую заданную точку параллельно двум неколлинеарным векторам.
Теорема доказана. |
|
Задача 3.3.1. |
В системе координат
|
Решение:
Из условия задачи следует, что
неколлинеарные векторы![]() и
и![]() параллельны искомой плоскости. Кроме
того, для радиус-вектора
параллельны искомой плоскости. Кроме
того, для радиус-вектора любой принадлежащей этой плоскости
точки вектор
любой принадлежащей этой плоскости
точки вектор![]() также будет ей параллелен.
также будет ей параллелен.
Из условия компланарности векторов
![]() ,
,![]() и
и![]() , получаем искомое уравнение плоскости,
имеющее вид
, получаем искомое уравнение плоскости,
имеющее вид![]() ,
или, в координатной форме (согласно
§2.7.)
,
или, в координатной форме (согласно
§2.7.)
 .
.
|
Задача 3.3.2. |
В
системе координат
|
Решение:
Из условия задачи следует, что
для радиус-вектора![]() любой точки, принадлежащей этой плоскости,
векторы
любой точки, принадлежащей этой плоскости,
векторы![]() и
и![]() будут ортогональны, т.е.
будут ортогональны, т.е.![]() .
.
В ортонормированнойсистеме координат
![]() это условие принимает вид
это условие принимает вид
![]()
или, обозначая
![]() ,
получим
,
получим![]() .
.
|
Следствие 3.3.1. |
Если
плоскость задана в ортонормированной
системе координат
|
|
Определение 3.3.2. |
Вектор
|
|
Определение 3.3.3. |
Вектор
|
В ортонормированной системе координат главный вектор плоскости является и нормальным ее вектором.
|
Задача 3.3.3. |
В
ортонормированной системе координат
|
|
Решение: |
1. ПустьKесть
ортогональная проекция точкиMна
данную плоскость, тогда
2. ТочкаKпринадлежит данной плоскости, поэтому
имеет место соотношение |
|
тогда для искомого расстояния получим
3. Рассмотрим теперьортонормированнуюсистему координат. В этом случае |
M
K
O
Рисунок 3.3.2. |
|
вектор
Поэтому
| |
|
Теорема 3.3.4. |
Плоскости
|
|
|
Доказательство:
Докажем достаточность. Если главные
векторы коллинеарны, то существует
такое число
может быть переписана в виде |
|
|
При
|
|
|
Докажем необходимость.
Пусть плоскости
Пусть для определенности этими
координатными плоскостями являются
плоскости, для которых
Параллельность этих прямых означает
существование
|
|
|
Рассматривая случай
но из условия
Теорема доказана. |
|
Следствие 3.3.2. |
Для того чтобы уравнения
были уравнениями одной и той же
плоскости, необходимо и достаточно,
чтобы существовало число
|
|
Определение 3.3.4. |
Пучком плоскостей в пространстве называется совокупность всех плоскостей, проходящих через данную прямую. |
|
Определение 3.3.5. |
Уравнением пучка плоскостей, проходящих через прямую, определяемую пересечением пары непараллельных плоскостей
называется уравнение вида
|
|
Определение 3.3.6. |
Связкой плоскостей в пространстве называется совокупность всех плоскостей, проходящих через данную точку. |
|
Определение 3.3.7. |
Если точка P, принадлежащая одновременно трем плоскостям
единственная, то уравнение вида
называется уравнением связки плоскостей, проходящих через точкуP. |
Для пучка и связки плоскостей в пространстве справедливы теоремы, аналогичные теореме 3.2.1. для пучка прямых на плоскости.















 .
.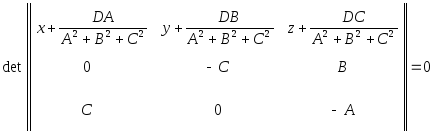 ,
, .
. .
.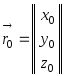 перпендикулярно ненулевому вектору
перпендикулярно ненулевому вектору .
.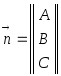 ортогонален этой плоскости.
ортогонален этой плоскости. до плоскости
до плоскости
 и,
следовательно,
и,
следовательно, ,
,

 будет нормальным вектором плоскости
будет нормальным вектором плоскости
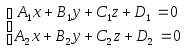
 .
.