§9.5. Экстремальные свойства квадратичных функционалов
Из
теоремы 9.2.1. следует существование в
базиса, в котором квадратичный функционал
имеет диагональный вид. Допустим, что
такой базис
построен так, что
и
.
Тогда имеет место
|
Теорема 9.5.1. |
Для
квадратичного функционала
|
в
справедливы соотношения
и
,при
условии, что компоненты x
удовлетворяют условию
.
|
|
Доказательство:
Если
в рассматриваемом базисе
Но
поскольку
Теорема доказана. |
,
то, в силу соотношений
,
будут иметь место неравенства
и
.
,
то будут справедливы и неравенства
и
.
То есть при
достигается максимум, а при
- минимум значений функционала.
§9.6. Полилинейные функционалы
По аналогии с билинейными функционалами, зависящими от пары элементов линейного пространства, можно определить нелинейные функционалы, обладающие аналогичными свойствами, но зависящие от большего числа аргументов.
|
Определение 9.6.1. |
Пусть
в линейном пространстве
|
каждой упорядоченной совокупностиk
элементов
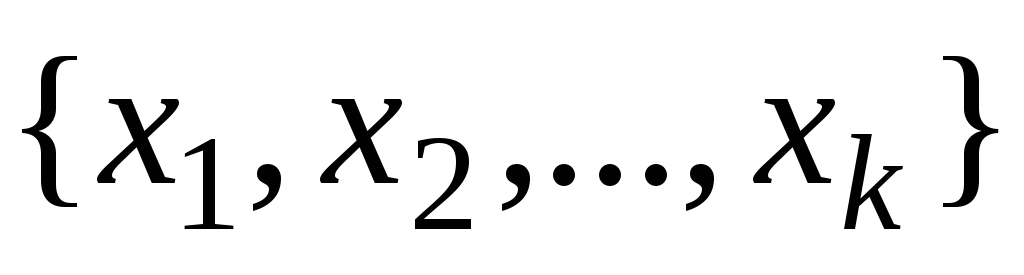поставлено в соответствие число
так, что для любогоj=[1,k]
|
|
тогда
говорят, что в
|
заданполилинейный
функционал,
а именно, k-линейный
функционал.
|
Пример 9.6.1. |
1.
Произведение k
линейных функционалов
2. Смешанное произведение трех векторов в трехмерном геометрическом пространстве является трилинейным функционалом.
3.
Определитель n-го
порядка есть полилинейный функционал
от n
элементов в
|
,
определенных в
,
то есть
,
естьk-линейный
функционал.
в случае, когда координатные представления
этих элементов являются столбцами
данного определителя.