
Раздел 12 44
Прикладные задачи линейной алгебры
Раздел 12
ПРИКЛАДНЫЕ ЗАДАЧИ ЛИНЕЙНОЙ АЛГЕБРЫ
В данном разделе рассматриваются некоторые классы задач, имеющие важное значение в прикладных разделах математики, таких как: математическая физика, теория оптимального управления, математическая экономика, вычислительная математика и т.д., причем общим для этих задач является использование в процессе их решения понятий и методов различных разделов линейной алгебры.
§12.1. Приведение квадратичных функционалов к диагональному виду
Задача отыскания базиса, в котором квадратичный функционал имеет диагональный или канонический вид, достаточно часто встречается в различных приложениях механики, физики, теории управления.
Приведение к диагональному виду квадратичного функционала, заданного в ортонормированном базисе
Пусть
в ортонормированном базисе
![]() евклидова пространства
евклидова пространства
![]() задан некоторый квадратичный функционал
задан некоторый квадратичный функционал
![]() .
Рассмотрим задачу отыскания в
.
Рассмотрим задачу отыскания в
![]() ортонормированного базиса
ортонормированного базиса
![]() ,
в котором функционал
,
в котором функционал
![]() имеет диагональный вид.
имеет диагональный вид.
Принципиальная
разрешимость подобной задачи для
неортонормированного базиса следует
из теоремы 9.2.1. Очевидно, что такой базис
не единственный, и потому представляется
интересным исследование возможности
построения в
![]() ортонормированного базиса, в котором
данный квадратичный функционал
ортонормированного базиса, в котором
данный квадратичный функционал
![]() имеет диагональный вид.
имеет диагональный вид.
Напомним
предварительно (см. §9.2.), что квадратичный
функционал в
![]() может быть задан формулой
может быть задан формулой
![]() ,
в которой симметрическая матрица
,
в которой симметрическая матрица
![]() преобразуется при переходе от базиса
преобразуется при переходе от базиса
![]() к базису
к базису
![]() по правилу
по правилу
![]() .
.
При доказательстве теоремы 9.2.1. использовалась математическая индукция в сочетании с методом выделения полных квадратов (называемым иногда методом Лагранжа), применение которого на практике малоудобно. Существенно более эффективным (с точки зрения минимизации затрат вычислительных усилий) представляется алгоритм, основой которого является
|
Теорема 12.1.1. |
Для всякого квадратичного функционала, заданного в ортонормированном базисе, существует ортонормированный базис, в котором этот функционал имеет диагональный вид 1). |
|
|
Доказательство:
1.
Как было показано в §9.2., матрица
квадратичного функционала
2.
Поскольку матрица перехода
3.
Формально симметрическая матрица
|
|
|
4.
Совпадение формул изменения матриц
квадратичного функционала и
самосопряженного оператора при
переходе от одного ортонормированного
базиса к другому позволяет использовать
в качестве базиса
Теорема доказана. |
Заметим, что утверждение теоремы 12.1.1. согласуется с утверждением следствия 10.7.4.
|
Определение 12.1.1. |
Линейный
самосопряженный оператор
|
При
этом очевидно выполнение равенства
![]()
![]() .
.
Используя теорему 12.1.1., можно упростить процедуру оценки экстремальных значений квадратичного функционала. В качестве примера рассмотрим задачу нахождения максимума и минимума для отношения Релея.
|
Определение 12.1.2. |
Функционал
|
|
Следствие 12.1.1. |
В
ортонормированном базисе максимальное
(минимальное) значение отношения Релея
равно максимальному (минимальному)
собственному значению оператора
|
|
|
Доказательство:
Поскольку
при переходе к ортонормированному
базису, образованному из собственных
векторов самосопряженного оператора
то,
проводя рассуждения, аналогичные
доказательству теоремы 9.5.1., получаем,
что
Следствие доказано. |
Проиллюстрируем применение теоремы 12.1.1. на примере решения следующей задачи:
|
Задача 12.1.1. |
При
помощи ортогонального оператора
привести к диагональному виду в
|
Решение:
1.
Пусть исходный ортонормированный базис
состоит из элементов
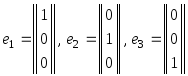 .
Восстановим по квадратичному функционалу
.
Восстановим по квадратичному функционалу
![]()
![]() порождающий его симметричный билинейный
функционал
порождающий его симметричный билинейный
функционал
![]() ,
использовав формулу
,
использовав формулу
![]() (см. определение 9.2.2.). В данном случае:
(см. определение 9.2.2.). В данном случае:
![]()
![]() ,
а
,
а
![]()
![]() ,
и потому
,
и потому
![]() ,
где
,
где
 и
и
 .
.
Следовательно,
матрица функционала
![]() имеет вид
имеет вид
 .
.
2.
Рассмотрим построенную симметрическую
матрицу как задающую самосопряженный
оператор
![]() в
в
![]() и найдем для него собственные значения.
Составляем характеристическое уравнение
8.5.2.
и найдем для него собственные значения.
Составляем характеристическое уравнение
8.5.2.
 или
или
![]() .
Оно имеет корни:
.
Оно имеет корни:
![]() ,
которые и являются собственными
значениями.
,
которые и являются собственными
значениями.
Заметим,
что, если нас интересует только
диагональный вид квадратичного
функционала, то его можно написать,
основываясь на следствии 10.7.1., как
 и на этом закончить решение задачи.
и на этом закончить решение задачи.
3.
В случае, когда требуется найти также
и матрицу
![]() - матрицу перехода от исходного
ортонормированного базиса к искомому,
необходимо построить собственные
векторы
- матрицу перехода от исходного
ортонормированного базиса к искомому,
необходимо построить собственные
векторы
оператора
![]() .
Для этого будем последовательно
подставлять найденные собственные
значения в систему (8.4.1.) и строить ее
общие решения.
.
Для этого будем последовательно
подставлять найденные собственные
значения в систему (8.4.1.) и строить ее
общие решения.
Для
![]() имеем:
имеем:
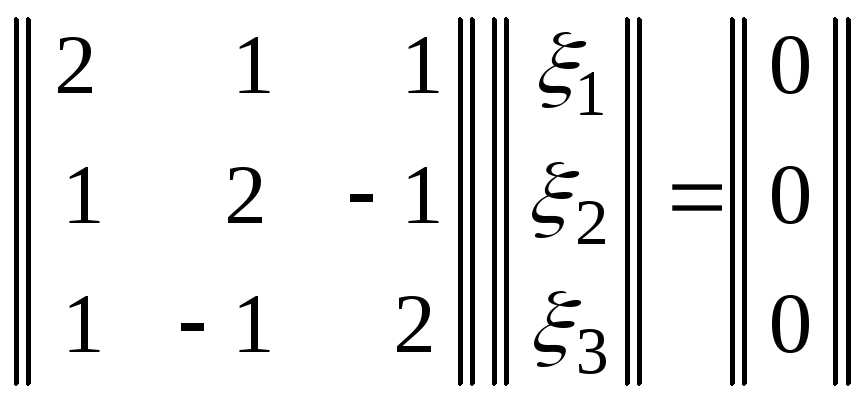 .
.
Заметим, что ранг основной матрицы этой системы равен 2, поскольку третье уравнение есть разность первых двух. Далее, действуя по схеме, описанной в §6.8. (метод Гаусса), получаем для компонентов собственного вектора систему условий
 .
.
Принимая
![]() за свободное неизвестное, получим
собственный вектор
за свободное неизвестное, получим
собственный вектор
 .
Кратность собственного значения
.
Кратность собственного значения
![]() равна 2, и в силу следствия 10.7.2. ему должны
отвечать два линейно независимых (но
не обязательно ортогональных) собственных
вектора. Конкретно, компоненты собственного
вектора должны удовлетворять следующей
системе уравнений:
равна 2, и в силу следствия 10.7.2. ему должны
отвечать два линейно независимых (но
не обязательно ортогональных) собственных
вектора. Конкретно, компоненты собственного
вектора должны удовлетворять следующей
системе уравнений:
 ,
,
из
которых независимое только одно
![]() .
Общее решение этой системы будет иметь
вид
.
Общее решение этой системы будет иметь
вид
 .
.
Каждый
столбец такого вида ортогонален
![]() ,
но выбранные конкретные фундаментальные
решения не ортогональны друг другу.
Поэтому пару ортогональных собственных
векторов, отвечающих
,
но выбранные конкретные фундаментальные
решения не ортогональны друг другу.
Поэтому пару ортогональных собственных
векторов, отвечающих
![]() ,
сформируем из первого фундаментального
решения и ортогональной ему линейной
комбинации первого и второго. Условие
ортогональности столбцов
,
сформируем из первого фундаментального
решения и ортогональной ему линейной
комбинации первого и второго. Условие
ортогональности столбцов
![]() и
и
 ,
очевидно, есть
,
очевидно, есть
![]() .
Откуда получаем
.
Откуда получаем
 и
и
 .
.
4. Отнормировав
базис
![]() ,
получим
,
получим
 ,
,
 и
и
 .
.
Матрица
 (перехода от базиса
(перехода от базиса
![]() к базису
к базису
![]() ),
столбцами которой являются координатные
разложения элементов базиса
),
столбцами которой являются координатные
разложения элементов базиса
![]() по базису
по базису
![]() ,
ортогональная, то есть удовлетворяет
соотношению
,
ортогональная, то есть удовлетворяет
соотношению![]() ,
что позволяет выписать формулы, выражающие
“новые” координаты через “старые”.
,
что позволяет выписать формулы, выражающие
“новые” координаты через “старые”.
Действительно
(см. 7.3.), из соотношения
 следует
следует
 или окончательно
или окончательно
 .
.
Приведение одним линейным оператором пары квадратичных функционалов, один из которых знакоопределенный, соответственно к каноническому и диагональному видам
Пусть
в некотором базисе
![]() линейного пространства
линейного пространства
![]() задана пара квадратичных функционалов
задана пара квадратичных функционалов
![]() и
и ![]() ,
первый из которых, например, положительно
определенный. Рассмотрим задачу отыскания
базиса
,
первый из которых, например, положительно
определенный. Рассмотрим задачу отыскания
базиса
![]() ,
в котором функционал
,
в котором функционал
![]() имеет канонический, а функционал
имеет канонический, а функционал ![]() - диагональный вид.
- диагональный вид.
Отметим, что условие положительной определенности одного из приводимых квадратичных функционалов существенно, поскольку в общем случае два различных квадратичных функционала одним линейным преобразованием к диагональному виду не приводятся 1)
Например,
квадратичный функционал
![]() в
в
![]() можно привести к диагональному виду
при помощи линейного оператора,
сводящегося к повороту плоскости
радиусов-векторов на угол .
При этом необходимо (см. доказательство
теоремы 4.4.1.), чтобы
удовлетворяло уравнению
можно привести к диагональному виду
при помощи линейного оператора,
сводящегося к повороту плоскости
радиусов-векторов на угол .
При этом необходимо (см. доказательство
теоремы 4.4.1.), чтобы
удовлетворяло уравнению
![]() .
Однако для пары квадратичных функционалов
.
Однако для пары квадратичных функционалов
![]() и
и
![]() угла ,
удовлетворяющего системе условий
угла ,
удовлетворяющего системе условий
![]() ,
,
очевидно не существует.
Опишем
теперь алгоритм приведения пары
квадратичных функционалов
![]() и
и ![]() ,
первый из которых положительно
определенный, соответственно к
каноническому и диагональному виду.
,
первый из которых положительно
определенный, соответственно к
каноническому и диагональному виду.
1.
Поскольку квадратичный функционал
![]() положительно определенный, то для него
существует в
положительно определенный, то для него
существует в
![]() базис, в котором он имеет канонический
вид, причем все его коэффициенты равны
единице. Приведем этот функционал к
данному виду каким-либо методом, например,
выделив полные квадраты с последующей
нормировкой. Одновременно тем же самым
методом преобразуем также и квадратичный
функционал
базис, в котором он имеет канонический
вид, причем все его коэффициенты равны
единице. Приведем этот функционал к
данному виду каким-либо методом, например,
выделив полные квадраты с последующей
нормировкой. Одновременно тем же самым
методом преобразуем также и квадратичный
функционал ![]() .
.
2.
Введем в
![]() скалярное произведение по формуле
скалярное произведение по формуле
![]() ,
превратив тем самым данное линейное
пространство в евклидово
,
превратив тем самым данное линейное
пространство в евклидово
![]() .
Отметим, что в этом случае базис, в
котором
.
Отметим, что в этом случае базис, в
котором
![]() имеет канонический вид, ортонормированный.
имеет канонический вид, ортонормированный.
3.
Построим затем третий, также
ортонормированный базис, переход к
которому выполняется при помощи матрицы
![]() ,
приведя квадратичный функционал
,
приведя квадратичный функционал ![]() к диагональному виду по схеме, описанной
в §12.1.1. При этом переходе квадратичный
функционал
к диагональному виду по схеме, описанной
в §12.1.1. При этом переходе квадратичный
функционал
![]() не потеряет канонического вида, поскольку
из условия
не потеряет канонического вида, поскольку
из условия
![]() и ортогональности
и ортогональности
![]() следует,
что
следует,
что
![]() .
.
Таким
образом, построен базис, в котором
квадратичный функционал
![]() имеет канонический вид, а функционал
имеет канонический вид, а функционал
![]() - диагональный.
- диагональный.
В
заключение отметим, что матрица перехода
к искомому ортонормированному базису
есть произведение ортогональной матрицы
![]() и матрицы перехода, при котором
положительно определенный квадратичный
функционал приводится к диагональному
виду.
и матрицы перехода, при котором
положительно определенный квадратичный
функционал приводится к диагональному
виду.
|
Задача 12.1.2. |
Найти
замену переменных, приводящую
квадратичные функционалы
|
Решение:
1.
Исследуем квадратичные функционалы
![]() и
и
![]() на знаковую определенность. Из критерия
Сильвестра (теорема 9.3.2.) и неравенств
на знаковую определенность. Из критерия
Сильвестра (теорема 9.3.2.) и неравенств
![]()
заключаем,
что
![]() - положительно определенный квадратичный
функционал, в то время как функционал
- положительно определенный квадратичный
функционал, в то время как функционал
![]() не является знакоопределенным.
не является знакоопределенным.
2.
Приведем методом Лагранжа квадратичный
положительно определенный функционал
![]() к каноническому виду. Поскольку
к каноническому виду. Поскольку
![]()
![]()
![]() ,
,
то,
выполнив замену переменных
 или
или
 ,
получим
,
получим
![]()
 и, соответственно,
и, соответственно,
![]()
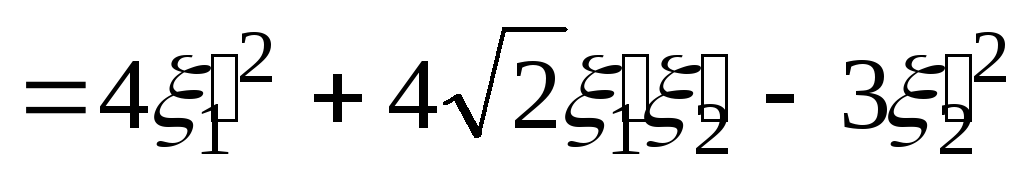 .
.
3.
Введение в
![]() скалярного произведения с единичной
матрицей Грама означает, что координаты
скалярного произведения с единичной
матрицей Грама означает, что координаты
![]() есть координаты евклидова пространства
есть координаты евклидова пространства
![]() с базисом
с базисом
![]() ,
где
,
где
![]() .
.
Матрица
квадратичного функционала
![]() в этом базисе
в этом базисе
![]() имеет собственные числа
имеет собственные числа
![]() и
и
![]() ,
а также ортонормированные собственные
векторы
,
а также ортонормированные собственные
векторы
 и
и
 ,
которые примем за новый базис
,
которые примем за новый базис
![]() .
.
4.
Матрица перехода от ортонормированного
базиса
![]() к ортонормированному базису
к ортонормированному базису
![]() ,
в котором
,
в котором
![]()
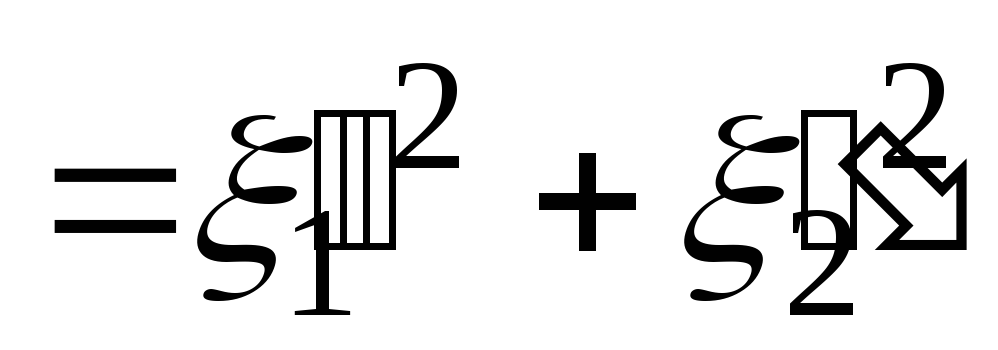 и
и
![]()
 ,
ортогональная и имеет вид
,
ортогональная и имеет вид
 .
.
Откуда
получаем, что
 и окончательно
и окончательно
 .
.
Если в задаче одновременного приведения пары квадратичных функционалов, один из которых положительно определенный, соответственно к диагональному и каноническому виду требуется найти лишь этот вид (а не формулы замены переменных), то возможно использование более простой схемы расчетов.
Допустим,
что положительно определенный квадратичный
функционал
![]() приведен при помощи матрицы перехода
приведен при помощи матрицы перехода
![]() к каноническому виду, то есть
к каноническому виду, то есть
![]() .
После того же преобразования матрица
квадратичного функционала
.
После того же преобразования матрица
квадратичного функционала
![]() будет иметь вид
будет иметь вид
![]() .
.
Согласно
теореме 12.1.1. в ортонормированном базисе
для построения диагонального вида
квадратичного функционала
![]() достаточно найти собственные числа
самосопряженного оператора, матрица
которого есть
достаточно найти собственные числа
самосопряженного оператора, матрица
которого есть
![]() .
Найдем выражение для этой матрицы,
учитывающее связь между матрицами
.
Найдем выражение для этой матрицы,
учитывающее связь между матрицами
![]() и
и
![]() .
.
Из
равенства
![]() следует, что
следует, что
![]() .
Тогда, используя правила обращения и
транспонирования произведения матриц,
перестановочность обращения и
транспонирования, а также симметричность
и невырожденность матрицы
.
Тогда, используя правила обращения и
транспонирования произведения матриц,
перестановочность обращения и
транспонирования, а также симметричность
и невырожденность матрицы
![]() ,
имеем
,
имеем

Полученное
равенство означает, что матрица
![]() может рассматриваться как результат
преобразования матрицы линейного
оператора
может рассматриваться как результат
преобразования матрицы линейного
оператора
![]() при замене базиса с матрицей перехода
при замене базиса с матрицей перехода
![]() .
Поскольку собственные значения линейного
оператора не зависят от выбора базиса,
то решение задачи сводится к определению
собственных значений оператора, имеющего
матрицу
.
Поскольку собственные значения линейного
оператора не зависят от выбора базиса,
то решение задачи сводится к определению
собственных значений оператора, имеющего
матрицу
![]() .
.
Собственные
векторы и собственные значения этого
оператора находятся согласно §8.5. из
системы линейных уравнений
![]() ,
которое можно преобразовать к виду
,
которое можно преобразовать к виду
![]() .
Условие существования ненулевых столбцов
.
Условие существования ненулевых столбцов
![]() :
:
![]()
есть
алгебраическое уравнение относительно
, корни которого и являются искомыми
коэффициентами диагонального представления
квадратичного функционала
![]() .
.
Проиллюстрируем применение данного метода для нахождения диагонального вида квадратичных форм в задаче 12.1.2.
Имеем
![]() и
и
![]() ,
то есть для определения коэффициентов
диагонального представления квадратичного
функционала
,
то есть для определения коэффициентов
диагонального представления квадратичного
функционала
![]() необходимо решить уравнение
необходимо решить уравнение
![]() или
или
![]() .
.
Поскольку
данное уравнение имеет два корня
![]() и
и
![]() ,
то искомый диагональный вид для
,
то искомый диагональный вид для
![]() будет
будет
![]()
 ,
в то время как очевидно, что
,
в то время как очевидно, что
![]()
 .
.

 ,
,