
- •Раздел 8 221
- •Раздел 8
- •§8.1. Линейные операторы
- •§8.2. Действия с линейными операторами
- •§8.3. Координатное представление линейных операторов
- •§8.4. Область значений и ядро линейного оператора
- •§8.5. Инвариантные подпространства и собственные векторы
- •§8.6. Свойства собственных векторов и собственных значений
- •§8.7. Линейные функционалы
§8.4. Область значений и ядро линейного оператора
Трактуя линейный оператор, действующий в линейном пространстве, как некоторое обобщение понятия функции, естественно рассмотреть вопрос об области определения и области значений линейных операторов.
Под
областью
значений линейного оператора
![]() будем понимать множество образоввсех
элементов
будем понимать множество образоввсех
элементов
![]() ,
то есть элементов вида
,
то есть элементов вида![]() .
В этом случае очевидно, что для любого
линейного оператора его область
определения совпадает с.
.
В этом случае очевидно, что для любого
линейного оператора его область
определения совпадает с.
Ответ на вопрос “Что представляет собой область значений линейного оператора?” дает
|
Теорема 8.4.1. |
Пусть
1.
Множество элементов
2.
Если, кроме того,
|
|
|
Доказательство:
Пусть
Пусть
теперь
|
|
|
линейности
каждый элемент из области значений
Выделим
из множества
Теорема доказана. |
|
Определение 8.4.1. |
Рангом
линейного оператора
|
Ранг
линейного оператора линейного оператора
![]() обозначается как
обозначается как![]() .
.
|
Следствие 8.4.1. |
|
|
Следствие 8.4.2. |
Размерность
области значений линейного оператора
|
|
|
Доказательство:
Поскольку
подпространство
Следствие доказано. |
|
Теорема 8.4.2. |
Ранг
произведения линейных операторов
|
|
|
Доказательство:
Рассмотрим
область значений линейного оператора
|
|
|
С
другой стороны, область значений
оператора
Теорема доказана. |
|
Теорема 8.4.3. |
Если
квадратная матрица
|
|
|
Доказательство:
Будем
рассматривать матрицы
Если
Теорема доказана. |
Замечания:
1.
Если матрица
![]() не квадратная, но существует одно из
произведений
не квадратная, но существует одно из
произведений
![]() или
или
![]() ,
то при
,
то при
![]() также верны равенства
также верны равенства
![]() или, соответственно,
или, соответственно,
![]() .
В этом можно убедиться, заменив матрицу
.
В этом можно убедиться, заменив матрицу
![]() матрицей
матрицей
![]() ,
являющейся дополнением нулевыми
столбцами или нулевыми строками
,
являющейся дополнением нулевыми
столбцами или нулевыми строками
![]() до квадратной так, чтобы существовали
до квадратной так, чтобы существовали
![]() или
или
![]() ,
ибо очевидно, что
,
ибо очевидно, что
![]() .
.
2. Ранг произведения матриц может быть меньше рангов каждого из сомножителей. Например:
![]() .
.
Другой
важной характеристикой линейного
оператора является совокупность
элементов линейного пространства
![]() ,
называемаяядром
линейного оператора и обозначаемая
,
называемаяядром
линейного оператора и обозначаемая
![]() .
.
|
Определение 8.4.2. |
Ядро
линейного оператора
|
|
Теорема 8.4.4. |
Если
|
|
|
Доказательство:
Непосредственной
проверкой можно убедиться, что для
Пусть
в базисе
С
другой стороны, поскольку каждое
решение однородной системы линейных
уравнений
Теорема доказана. |
Линейные отображения
Как было отмечено в §8.1., в тех случаях, когда область значений оператора не принадлежит области определения, следует говорить об отображении.
В §7.5. было использовано понятие взаимно однозначного отображения, называемого иногда биекцией. Для отображений также выделяются специальные случаи так называемых инъективных и сюръективных отображений. Рассмотрим эти случаи подробнее.
|
Определение 8.4.3. |
Отображение
|
В
случае инъекции множество всех значений
оператора
![]() может не совпадать с.
может не совпадать с.
|
Определение 8.4.4. |
Отображение
|
В случае сюръекции прообраз любого элемента из всегда существует в , но, вообще говоря, он не единственен.
В таблице 8.4.1. приведены сравнительные примеры отображений различных типов.
|
Тип отображения
|
Инъективное |
Неинъективное |
|
Сюръективное
|
|
|
|
Несюръективное
|
|
|
Таблица 8.4.1.
Рассмотрим
теперь линейный оператор
![]() ,
отображающий элементы
,
отображающий элементы
![]() в элементы
в элементы
![]() ,
то есть отображение, для которого
,
то есть отображение, для которого
![]() ,
а
,
а
![]() .
Допустим, что
.
Допустим, что
![]() есть
есть
базис
в
![]() ,
а
,
а
![]() - базис в
- базис в
![]() .
Тогда можно сделать следующее обобщение
определения 8.3.1.
.
Тогда можно сделать следующее обобщение
определения 8.3.1.
|
Определение 8.4.5. |
Матрица
|
Отметим,
что в конечномерном случае сюръективность
отображения означает выполнение условия
![]() ,
а инъективность - условия
,
а инъективность - условия
![]() .
Отсюда следует, что ранг матрицы линейного
оператора, являющегося сюръективным
отображением, равен числу ее строк, а
ранг матрицы инъективного отображения
равен числу ее столбцов. Наконец,
отображение, являющееся одновременно
и инъективным и сюръективным, будет
взаимно однозначным - или биекцией (см.
определение 5.2.4.).
.
Отсюда следует, что ранг матрицы линейного
оператора, являющегося сюръективным
отображением, равен числу ее строк, а
ранг матрицы инъективного отображения
равен числу ее столбцов. Наконец,
отображение, являющееся одновременно
и инъективным и сюръективным, будет
взаимно однозначным - или биекцией (см.
определение 5.2.4.).
Из
определения 8.4.5. следует, что матрица
линейного отображения зависит как от
выбора базиса
![]() ,
так и от выбора базиса
,
так и от выбора базиса![]() .
Правило изменения этой матрицы при
замене базисов дает
.
Правило изменения этой матрицы при
замене базисов дает
|
Теорема 8.4.5. |
Матрица
линейного отображения
где
|
|
|
Доказательство: Аналогично доказательству теоремы 8.3.2. |
В общем случае, исследование свойств оператора, у которого область значений не содержится в области его определения, может оказаться достаточно сложной задачей. Если же область значений имеет конечную размерность, не превышающую размерность области определения, то, пользуясь теоремой 7.5.1. (об изоморфизме), можно попытаться свести исследование отображения к исследованию преобразования, установив изоморфизм между областью значений отображения и некоторым подпространством области его определения.
|
Пример 8.4.1. |
1. Оператор
Отметим, что, хотя в данном случае и отображение и преобразование реализуют геометрически одну и ту же функцию, вид задающих их матриц может быть различным.
Например,
пусть в ортонормированной системе
координат
2.
Пусть линейный оператор
Исследование
свойств данного отображения можно
свести к исследованию свойств
преобразования, ставящего в соответствие
квадратным матрицам
|
|
|
|
|
Задача 8.4.1. |
Линейное
отображение
|
Решение:
1.
Пусть координатное представление
прообраза преобразования
![]() есть
есть
 ,
а координатное представление образа -
,
а координатное представление образа - .
Тогда ядро - множество элементовx
таких, что
.
Тогда ядро - множество элементовx
таких, что
![]() ,
задается в координатном представлении
системой линейных уравнений
,
задается в координатном представлении
системой линейных уравнений
![]() или
или
 ,
общее решение которой есть
,
общее решение которой есть
 .
Отсюда заключаем, что ядро линейного
отображения
.
Отсюда заключаем, что ядро линейного
отображения
![]() есть линейная оболочка элемента
есть линейная оболочка элемента
 ,
и поскольку оно не состоит только из
нулевого элемента, то данное отображение
неинъективное.
,
и поскольку оно не состоит только из
нулевого элемента, то данное отображение
неинъективное.
Заметим,
что к этому же заключению можно прийти,
приняв во внимание, что
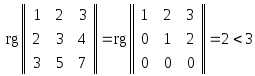 - числа столбцов матрицы отображения.
- числа столбцов матрицы отображения.
2.
Область значений линейного отображения
![]() состоит из элементов
состоит из элементов
![]() таких, что
таких, что
![]() .
В координатной форме принадлежность
элемента
.
В координатной форме принадлежность
элемента
![]() к множеству значений означает совместность
системы линейных уравнений
к множеству значений означает совместность
системы линейных уравнений
 ,
,
следовательно,
нам необходимо выяснить, при каких
значениях
![]() данная система линейных уравнений
совместна. Это можно сделать, например,
при помощи теоремы 6.6.1. (Кронекера-Капелли),
сравнив ранги основной и расширенной
матриц данной системы.
данная система линейных уравнений
совместна. Это можно сделать, например,
при помощи теоремы 6.6.1. (Кронекера-Капелли),
сравнив ранги основной и расширенной
матриц данной системы.
Из условия
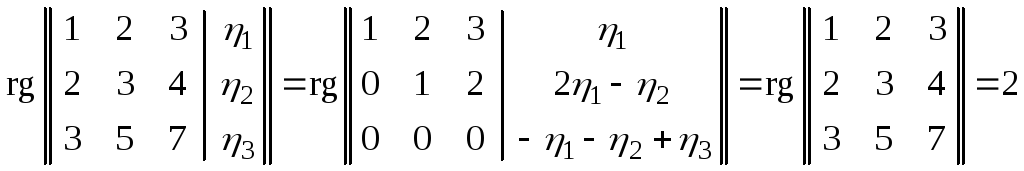
найдем,
что для совместности необходимо и
достаточно, чтобы
![]() ,
что, в свою очередь, означает, что
множество значений отображения
,
что, в свою очередь, означает, что
множество значений отображения
![]() состоит из элементов вида
состоит из элементов вида
 ,
,
являющихся
решениями уравнения
![]() .
.
Заметим,
наконец, что поскольку не каждый элемент
![]() имеет прообраз в
имеет прообраз в![]() ,
то данное отображение не является и
сюръективным.
,
то данное отображение не является и
сюръективным.

 ядру оператора
ядру оператора



















 ,
то есть матрица данного преобразования
имеет вид
,
то есть матрица данного преобразования
имеет вид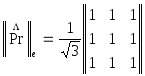 .
Но, с другой стороны, приняв
.
Но, с другой стороны, приняв .
Найти его ядро и множество значений.
Выяснить, является ли данное отображение
инъективным или сюръективным.
.
Найти его ядро и множество значений.
Выяснить, является ли данное отображение
инъективным или сюръективным.