
Раздел 4 105
Нелинейные объекты на плоскости и в пространстве
Раздел 4
НЕЛИНЕЙНЫЕ ОБЪЕКТЫ
НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
§4.1. Линии на плоскости и в пространстве
Пусть
дана система координат
![]() на плоскости и числовое множество
на плоскости и числовое множество![]() ,
являющееся отрезком или интервалом
(возможно, бесконечным или полубесконечным).
,
являющееся отрезком или интервалом
(возможно, бесконечным или полубесконечным).
|
Определение 4.1.1. |
Будем
говорить, что линия L
на плоскости задана параметрически
вектор-функцией
1.
Для любого
2.
Для любой точки
|
Иногда
линия на плоскости задается в виде
уравнения
![]() ,
которое получается исключением параметра
из системы уравнений
,
которое получается исключением параметра
из системы уравнений
 .
.
|
Пример 4.1.1. |
1.
Прямая линия задается вектор-функцией
|
|
. |
или
2.
В декартовой ортонормированной системе
координат окружность радиуса R
с
центром в точке
или
же уравнением
|
|
Определение 4.1.2. |
Линия
называется алгебраической,
если ее уравнение в декартовой системе
координат имеет вид
|
|
Определение 4.1.3. |
Число
|
|
Пример 4.1.2. (алгебраические линии) |
Прямая
Квадратная парабола
Гипербола
“Декартов лист” |
|
(N=1)
(N=2)
(N=2)
(N=3). |
|
Теорема 4.1.1. |
Порядок алгебраической линии не зависит от выбора системы координат. |
|
|
Доказательство:
Пусть
алгебраическая линия L
имеет в системе координат
поэтому уравнение линии L в “новой” системе координат будет
Отсюда
следует, в силу определения 4.1.2., что
Теорема доказана. |
Замечание: фигуры на плоскости можно задавать, используя ограничения типа неравенств.
|
Пример 4.1.4. |
1.
В ортонормированной системе координат
набор условий
2.
Неравенство вида
|
Рассмотрим
теперь случай линии в пространстве.
Пусть дана пространственная система
координат
![]() .
.
|
Определение 4.1.4. |
Будем
говорить, что линия L
в пространстве задана параметрически
вектор-функцией
|
|
|
определенные
для
1.
Для любого
2.
Для любой точки
|
Иногда
линия в пространстве задается системой
уравнений
![]() ,
которая получается исключением параметра
из соотношений
,
которая получается исключением параметра
из соотношений
 ,
или же равносильным уравнением, например,
вида
,
или же равносильным уравнением, например,
вида![]() .
.
|
Пример 4.1.3. |
1.
В декартовой системе координат
алгебраическая линия второго порядка
2.
В ортонормированной системе координат
винтовая линия радиуса R с шагом
|

 ,
где
,
где ,
то есть
,
то есть
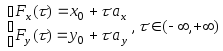
 ,
то есть
,
то есть

 ,
, задает
прямоугольный равнобедренный
треугольник, катеты которого лежат
на осях координат и имеют длины 3.
задает
прямоугольный равнобедренный
треугольник, катеты которого лежат
на осях координат и имеют длины 3. ,
где
,
где ,
или же
,
или же
