4.3 Определение геометрических и кинематических параметров быстроходной ступени редуктора (колеса косозубые)

Межосевое расстояние быстроходной ступени , мм, определяем по формуле:

, (4.56)

.

Модуль зацепления , мм, рассчитываем по формуле:

, (4.57)

.

После согласования со стандартными значениями

Число зубьев для шестерни рассчитываем по формуле:

(4.58)

Угол наклона зубьев первоначально принимается любое из интервала от 8^ до 18^.

Значение числа зубьев для шестерни округляем до целого числа:

Число зубьев для колеса рассчитываем по формуле:

, (4.59)

.

Значение числа зубьев для колеса округляем до целого числа:

Уточненное значение угла наклона зубьев, град:

, (4.60)

.

Делительный диаметр шестерни , мм, рассчитываем по формуле:

, (4.61)

.

Делительный диаметр колеса , мм, рассчитываем по формуле:

, (4.62)

.

Диаметр вершины зубьев шестерни , мм, рассчитываем по формуле:

, (4.63)

Диаметр вершины зубьев колеса , мм, рассчитываем по формуле:

, (4.64)

.

Диаметр впадин зубьев шестерни , мм, рассчитываем по формуле:

, (4.65)

.

Диаметр вершины зубьев колеса 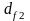, мм, рассчитываем по формуле:

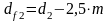, (4.66)

.

Рабочую ширину зубчатого венца колеса , мм, рассчитываем по формуле:

, (4.67)

Согласовываем со стандартными значениями:

Рабочую ширину зубчатого венца шестерни , мм, рассчитываем по формуле:

(4.68)

Согласовываем со стандартными значениями:

Окружную скорость зубчатых колес , м/с, рассчитываем по формуле:

, (4.69)

.

Из таблицы «Степень точности цилиндрических зубчатых передач» по ГОСТ 1643-81 выбираем по рекомендации степень точности 8.

4.3.1 Проверочный расчет зубьев колес на контактную прочность

Рабочее контактное напряжение , МПа, рассчитываем по формуле:

(4.70)

Коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления , рассчитываем по формуле:

(4.71)

где – делительный угол профиля в торцовом сечении, град, рассчитываем по формуле:

(4.72)

Для передач без смещения .

– основной угол наклона, град, рассчитываем по формуле:

(4.73)

Из формулы (4.71) находим значение коэффициента :

Коэффициент, учитывающий суммарную длину контактных линий косозубой передачи , рассчитываем по формуле:

(4.74)

– коэффициент торцового перекрытия для передач без смещения при < 20, рассчитываем по формуле:

, (4.75)

.

Из формулы (4.74) находим значение коэффициента :

Окружную силу на делительном диаметре шестерни , Н, рассчитываем по формуле:

, (4.76)

.

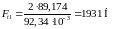Коэффициент, учитывающий динамическую нагрузку , рассчитываем по формуле:

(4.77)

где – удельную окружную динамическую силу, Н/мм, рассчитываем по формуле:

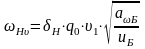, (4.78)

где – коэффициент, учитывающий влияние вида зубчатой передачи, равен 0,02

.

Из формулы (4.77) находим значение коэффициента :

Коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий , рассчитываем по формуле:

(4.79)

– коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий в начальный период работы передачи, рассчитываем по формуле:

(4.80)

Удельную нормальную жесткость пары зубьев , Н/мммкм, рассчитываем по формуле:

, (4.81)

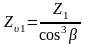, (4.82)

,

, (4.83)

.

Из формулы (4.81) находим значение удельной нормальной жесткости пары зубьев , Н/мммкм:

Коэффициент, учитывающий приработку зубьев , рассчитываем по формуле:

, (4.84)

.

Из формулы (4.80) находим значение коэффициента :

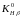Из формулы (4.79) находим значение коэффициента :

– коэффициент, учитывающий распределение нагрузки между зубьями, рассчитываем по формуле:

, (4.85)

где – суммарный коэффициент перекрытия рассчитываем по формуле:

(4.86)

– коэффициент торцового перекрытия рассчитываем по формуле:

(4.87)

где

, (4.88)

. (4.89)

где – углы профиля зуба в точках на окружностях вершин, град, рассчитываем по формулам:

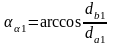, (4.90)

. (4.91)

где – основные диаметры шестерни и колеса, мм, рассчитываем по формулам:

, (4.92)

, (4.93)

,

.

Из формулы (4.90) находим значение угла , град:

Из формулы (4.91) находим значение угла , град:

Из формулы (4.88) находим значение коэффициента :

Из формулы (4.89) находим значение коэффициента :

Из формулы (4.87) находим значение коэффициента :

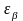– коэффициент осевого перекрытия рассчитываем по формуле:

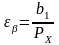(4.94)

где – осевой шаг, мм, рассчитываем по формуле:

(4.95)

Из формулы (4.94) находим значение коэффициента :

Из формулы (4.86) находим значение коэффициента :

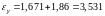
– среднюю удельную торцевую жесткость зубьев пары зубчатых колес, Н/мммкм, рассчитываем по формуле:

, (4.96)

.

– коэффициент, учитывающий статистическое распределение погрешностей и критерии допустимого повреждения активных поверхностей зубьев, равен 0,2

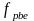– предельное отклонение шага зацепления, мкм, рассчитываем по формуле:

(4.97)

где – равны 22 мкм и 26 мкм соответственно, выбрав из таблицы «Предельные отклонения шага зацепления , мкм, (из ГОСТ 1643-81)»

Из формулы (4.97) находим значение предельного отклонения шага зацепления , мкм:

– уменьшение погрешности шага зацепления в результате приработки, мкм, рассчитываем по формуле:

, (4.98)

где

, (4.99)

, (4.100)

, (4.101)

, (4.102)

,

.

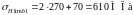Из формулы (4.99) находим значение :

Из формулы (4.100) находим значение :

Из формулы (4.98) находим значение уменьшения погрешности шага зацепления в результате приработки , мкм:

Из формулы (4.85) находим значение коэффициента :

Из формулы (4.70) находим значение рабочего контактного напряжения , МПа:

,

Допускаемое контактное напряжение , МПа, для косозубой передачи принимают в качестве допускаемого контактного напряжения зубчатого колеса:

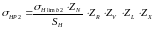(4.103)

где – предел контактной усталости поверхности зубьев, соответствующий базовому числу циклов напряжений колеса, МПа

(4.104)

где – твердость материала колеса (таблица 1)

– коэффициент долговечности

(4.105)

где – базовое число циклов напряжений, соответствующее пределу выносливости, миллионов циклов

(4.106)

– суммарное число циклов напряжений, миллионов циклов

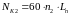, (4.107)

где – ресурс (долговечность) передачи, ч

Из формулы (4.105) находим значение коэффициента долговечности :

При выполнении расчетов принимаем равным 0,9.

– коэффициент, учитывающий влияние исходной шероховатости сопряженных поверхностей зубьев,

– коэффициент, учитывающий влияние скорости,

– коэффициент, учитывающий влияние смазочного материала,

– коэффициент, учитывающий размер зубчатого колеса.

Коэффициент запаса прочности равен 1,1.

Из формулы (4.103) находим значение допускаемого контактного напряжения зубчатого колеса:

После данных расчетов условие (4.37) выполняется.