4.2.2 Расчет зубьев на прочность при изгибе

Выносливость зубьев, необходимую для предотвращения усталостного излома, устанавливают для каждого колеса сопоставлением расчетного местного напряжения от изгиба в опасном сечении на переходной поверхности и допускаемого напряжения:

(4.37)

Расчетное местное напряжение при изгибе для шестерни , МПа, рассчитываем по формуле:

(4.38)

где – коэффициент нагрузки рассчитываем по формуле:

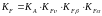(4.39)

где – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса, рассчитываем по формуле:

(4.40)

где 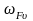– удельную окружную динамическую силу, Н/мм, рассчитываем по формуле:

(4.41)

где – коэффициент, учитывающий влияние вида зубчатой передачи, равен 0,16

Из формулы (4.40) находим значение коэффициента :

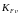– коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий, рассчитываем по формуле:

, (4.42)

, (4.43)

, (4.44)

.

Из формулы (4.43) находим значение коэффициента :

Из формулы (4.42) находим значение коэффициента :

– коэффициент, учитывающий распределения нагрузки между зубьями, равен коэффициенту , который равен 1

Из формулы (4.39) находим значение коэффициента :

– коэффициенты, учитывающие форму зуба и концентрацию напряжений, равные 3,9 и 3,613 соответственно для шестерни и колеса в зависимости от числа зубьев

– коэффициент, учитывающий наклон зуба прямозубых передач, равен 1

– коэффициент, учитывающий перекрытие зубьев, равен 1

Из формулы (4.38) находим значение расчетного местного напряжения при изгибе для шестерни , МПа:

Расчетное местное напряжение при изгибе для колеса , МПа, рассчитываем по формуле:

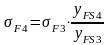, (4.45)

.

Допускаемое напряжение , МПа, рассчитываем по формуле:

(4.46)

где – предел выносливости зубьев при изгибе, МПа, рассчитываем по формуле:

(4.47)

где – пределы выносливости зубьев при изгибе для шестерни и колеса соответственно, МПа, рассчитываем по формулам:

, (4.48)

,

, (4.49)

.

– коэффициент, учитывающий технологию изготовления зубчатых колес, равен 1

– коэффициент, учитывающий способ получения заготовки зубчатого колеса, равен 1

– коэффициент, учитывающий отсутствие шлифовки переходной поверхности зубьев, равен 1

– коэффициент, учитывающий отсутствие деформационного упрочнения или электрохимической обработки переходной поверхности, равен 1

– коэффициент, учитывающий влияние характера приложения нагрузки (односторонняя), равен 1

Из формулы (4.47) находим значение предела выносливости зубьев при изгибе для шестерни , МПа:

Из формулы (4.47) находим значение предела выносливости зубьев при изгибе для колеса , МПа:

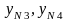– коэффициенты долговечности для шестерни и колеса соответственно рассчитываем по формулам:

(4.50)

(4.51)

где – базовое число циклов напряжения равное 410⁶

– показатель степени для зубчатых колес с однородной структурой материала равен 6

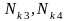– суммарные числа циклов напряжений, определяемые для шестерни и колеса, миллионов циклов, рассчитываем по формулам:

, (4.52)

,

, (4.53)

.

Т.к. , то принимаем за 1.

– коэффициент, учитывающий чувствительность материала к концентрации напряжений, рассчитываем по формуле:

, (4.54)

.

– коэффициент, учитывающий шероховатость переходной поверхности (при нормализации и улучшении), равен 1,2

– коэффициенты, учитывающие размеры зубчатого колеса, рассчитываем по формулам:

, (4.55)

,

.

– коэффициент запаса прочности для углеродистой и легированной сталей, подвергнутых нормализации или улучшению, равен 1,7

Из формулы (4.46) находим значение допускаемого напряжения для шестерни , МПа:

Из формулы (4.46) находим значение допускаемого напряжения для колеса , МПа:

После данных расчетов условие (4.37) выполняется.