4.2.1 Проверочный расчет зубьев колес на контактную прочность

После определения геометрических размеров рабочие поверхности зубьев необходимо проверить на контактную прочность. Для этого следует определить рабочее контактное напряжение и сравнить с допускаемым . Должно выполняться условие:

(4.24)

Определим рабочее контактное напряжение , МПа:

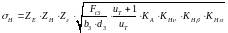(4.25)

где – коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес, изготовленных из стали, равен 190

– коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления, рассчитываем по формуле:

(4.26)

где – делительный угол профиля в торцовом сечении, град

– угол зацепления, град

Для прямозубых передач без смещения:

Из формулы (4.26) находим значение коэффициента :

– коэффициент, учитывающий суммарную длину контактных линий прямозубой передачи, рассчитываем по формуле:

(4.27)

где – коэффициент торцового перекрытия рассчитываем по формуле:

, (4.28)

.

Из формулы (4.27) находим значение коэффициента :

Окружную силу на делительном диаметре шестерни , Н, рассчитываем по формуле:

, (4.29)

.

– коэффициент внешней динамической нагрузки при равномерном нагружении двигателя и ведомой машины равен 1,1

– коэффициент, учитывающий динамическую нагрузку, рассчитываем по формуле:

(4.30)

где – удельная окружная динамическая сила, Н/мм

(4.31)

где – коэффициент, учитывающий влияние вида зубчатой передачи, равен 0,06

– коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса 8-й степени точности, равен 6,1, т.к. по условию .

Из формулы (4.30) находим значение коэффициента :

– коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий, рассчитываем по формуле:

(4.32)

– коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий в начальный период работы передачи, рассчитываем по формуле:

(4.33)

где – фактическое отклонение положения контактных линий в начальный период работы передачи, рассчитываем по формуле:

(4.34)

где – коэффициент, учитывающий статистическое распределение погрешностей и критерии допустимого повреждения активных поверхностей зубьев, равен 0,3

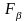– допуск на погрешность направления зубьев равен 32 мкм по таблице «Допуск на погрешность направления зубьев (ГОСТ 1643-81)»

Из формулы (4.34) находим значение фактического отклонения положения контактных линий в начальный период работы передачи :

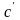– удельную нормальную жесткость пары зубьев, Н/мммкм, рассчитываем по формуле:

(4.35)

где – эквивалентные числа зубьев шестерни и колеса соответственно

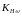– коэффициент, учитывающий приработку зубьев

, (4.36)

.

Из формулы (4.29) находим значение коэффициента :

Из формулы (4.32) находим значение коэффициента :

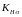– коэффициент, учитывающий распределение нагрузки между зубьями прямозубых передач, равен 1

Из формулы (4.25) находим значение рабочего контактного напряжение , МПа:

,

.

После данных расчетов условие (4.24) выполняется.