§11.5. Соотношение неопределенностей
Для
эрмитовых операторов, действующих в
унитарном пространстве, справедлива
|
Теорема
11.5.1.
(Соотношение неопределен-
ностей) |
Для
двух эрмитовых операторов
 и
и
 ,
заданных в унитарном пространстве,
имеет место соотношение: ,
заданных в унитарном пространстве,
имеет место соотношение:
 . . |
|
|
Доказательство:
1.
Рассмотрим оператор
 (где
- некоторый вещественный параметр),
для которого эрмитово сопряженным
будет оператор вида (где
- некоторый вещественный параметр),
для которого эрмитово сопряженным
будет оператор вида
 , ,
ибо
эрмитовыми являются следующие четыре
оператора:
 .
Заметим также, что оператор .
Заметим также, что оператор - эрмитов и что - эрмитов и что .
(См. доказательство теоремы 10.8.2., пункт
1.) .
(См. доказательство теоремы 10.8.2., пункт
1.)
2.
Выразим оператор
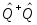 через операторы через операторы ,
получим: ,
получим:

3.
Обозначим
 ,
причем отметим, что из предыдущего
равенства следует эрмитовость оператора ,
причем отметим, что из предыдущего
равенства следует эрмитовость оператора как линейной комбинации эрмитовых
операторов. Подсчитаем теперь среднее
значение эрмитова оператора как линейной комбинации эрмитовых
операторов. Подсчитаем теперь среднее
значение эрмитова оператора : :
 . .
Полученное
значение
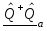 есть вещественный квадратный трехчлен
относительно,
который должен быть неотрицательным
при любом .
Отсюда следует, что его дискриминант
неположителен, то есть есть вещественный квадратный трехчлен
относительно,
который должен быть неотрицательным
при любом .
Отсюда следует, что его дискриминант
неположителен, то есть
 ,
или окончательно ,
или окончательно
 . .
Теорема
доказана. |
1)
Определение и основные свойства
комплексных чисел приводятся в приложении
3.


