LECT17

Лекция № 17 (18.04.00)

Замкнутые классы

1) Обозначим через - класс всех булевых функций , сохраняющих константу 0, т.е. функций, для которых выполняется равенство .

При добавлении несущественной переменной равенство не меняется.

Функции,

.

Количество таких функций (n – число переменных) т.к. в первой строке всегда содержит 0. (У второй половины 1).

T₀ – замкнутый класс, т.к. если

, то

.

2) Обозначим через - класс всех булевых функций , сохраняющих константу 1, т.е. функций, для которых выполняется равенство .

Класс вместе с любой функцией содержит равную ей функцию.

Функции ,

.

Класс состоит из функций двойственных классу (следует из определения).

Поэтому все свойства класса переносятся на класс .

.

3) S – класс – класс всех самодвойственных функций, т.е. .

Функции ,

, т.к.

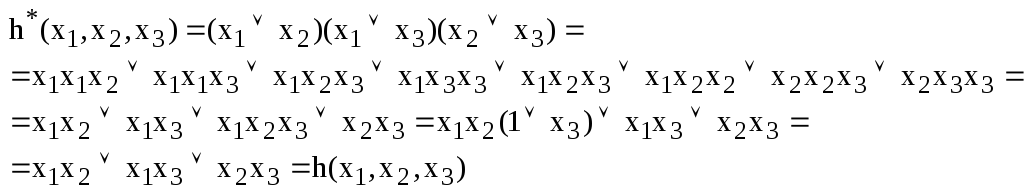Для самодвойственной функции имеет место тождество

.

Тем самым на наборах и ф-я принимает противоположные значения (определяется половиной комбинаций x_i). Поэтому число самодвойственных функций равно .

Докажем, что класс S замкнут.

Пусть , , т.е. . Тогда

.

4. Обозначим

, , .

опр || Для 2^х наборов и выполнено отношение предшествования , если .

Пример.

Очевидно, что если.

Таким образом, множество всех наборов длины n по отношению к операции предшествования является частично упорядоченным.

Опр. || функция называется монотонной, если для любых 2^х наборов таких, что выполняется неравенство

.

Монотонные функции:

,

- не монотонная

Обозначим M – множество всех монотонных функций. Нужно доказать, что этот класс замкнутый.

Пусть , , .

Будем считать, что все f_i зависят от x₁, x_n.

Пусть два набора переменных длины n, причем . Тогда,

………………

, следовательно

, тогда и

.

Тем самым .

5) L – класс всех линейных функций

О полноте этого класса мы упоминали ранее.

Эти замкнутые классы не тождественны и они не полны, что следует из таблицы

	T0	T1	S	M	L
0	+	-	-	+	+
1	-	+	-	+	+
	-	-	+	-	+

Теорема о функциональной полноте.

Для того, чтобы система функций была полной, необходимо и достаточно, чтобы она целиком не содержалась ни в одном из 5 замкнутых классов T₀, T₁, S, M, L.

(Без док-ва).

Опр. Класс R из (множество всех булевых функций) называется предполным или максимальным, если для любой ф-ции f () класс полный.

В алгебре логики только 5 предполных классов: .

Пример.

система полна.

С другой стороны, удаление любой из функций приводит к неполной системе

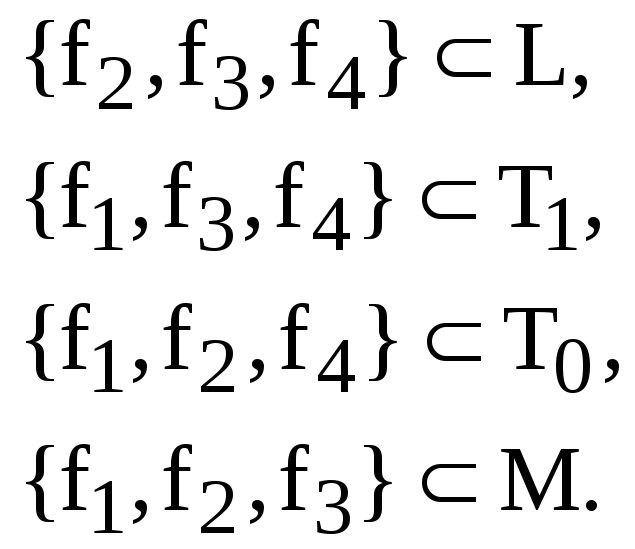
Пример 2.

Система функций B={x₁x₁}, полна так как не сохраняет константы, не линейна, не самодвойственна () и не монотонна (последний ноль – после 1).

Теорема || из всякой полной в системы функций B можно выделить полную подсистему, содержащую не более 4^х функций.

(Без док-ва).

Понятия многозначной логики.

Оценка погрешности.

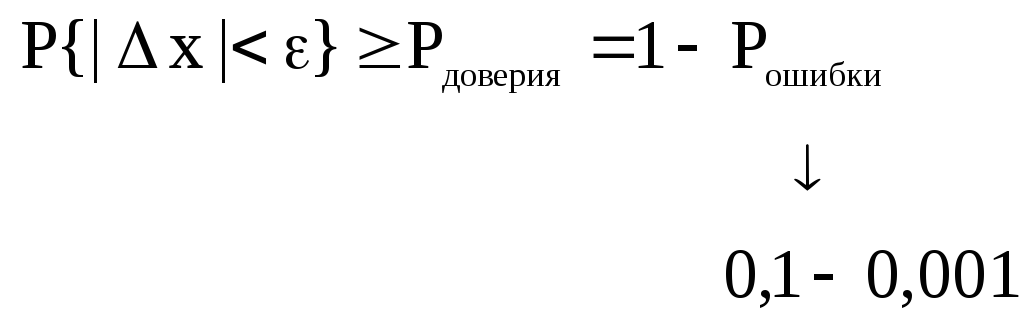
k – знач. логика

k – катур. Число

множество значений, которые может принимать функция

опр || называется k-значной логикой, если в наборе значения переменных , где значение

Элемент функции k-значной логики

1) константы: 0,1,…,k-1

2) отрицание Роста:

3) отрицание Лукасевича:

4) Характеристическая функция I^го рода

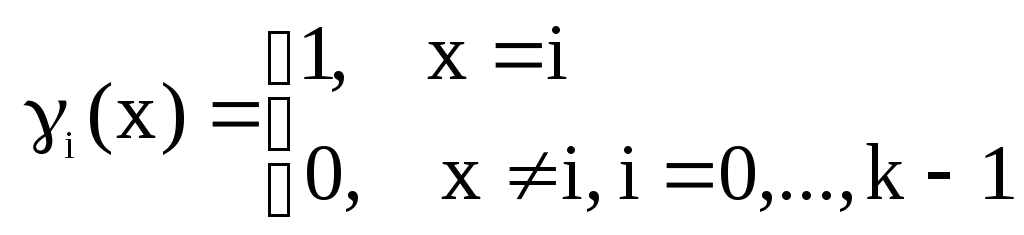
5) Характеристическая функция 2^го рода:

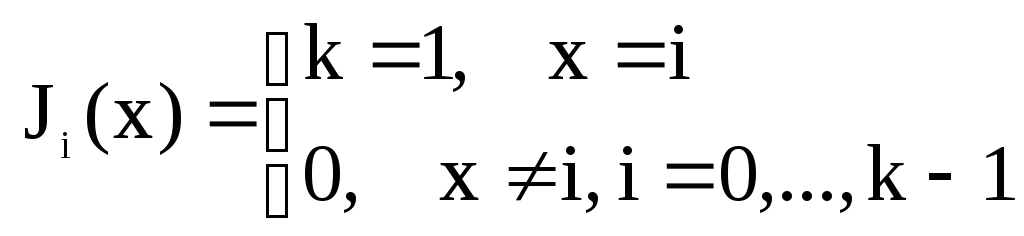
6)

7)

8) сумма по модулю k

9) произведение

10) усеченная разность

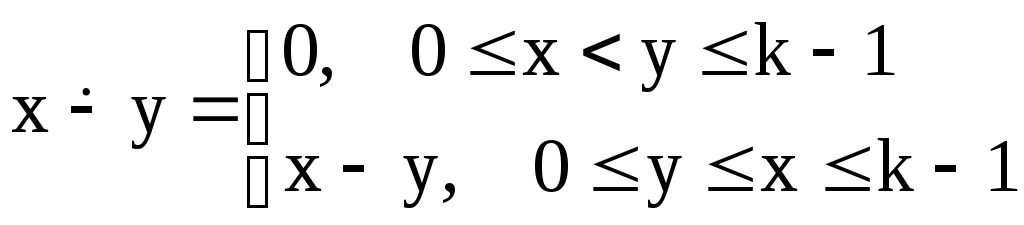
11)

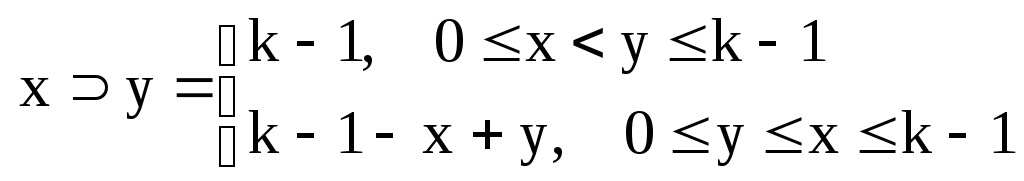
12) Функция Вебба:

13)

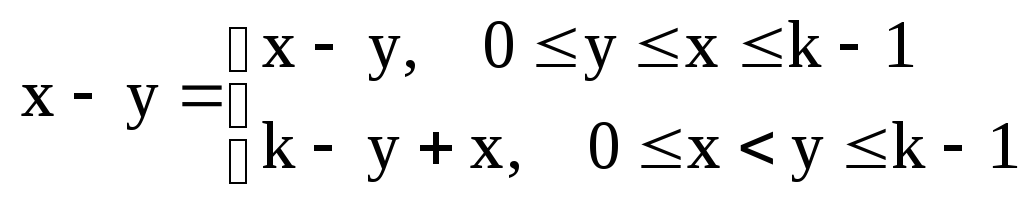
Свойство функций:

выполняются свойства коммутативности и ассоциативности, дистрибутивность, умножение относительно сложения

Дистрибутивность операции max относительно min

x	y	z	I	II
1	2	3	z	z
1	3	2	z	z
2	1	3	z	z
2	3	1	x	x
3	1	2	z	z
3	2	1	y	y
1	1	1	1	1
1	2	2	2	2
2	1	2	2	2
3	2	1	2	2

Дистрибутивность операции min относительно max

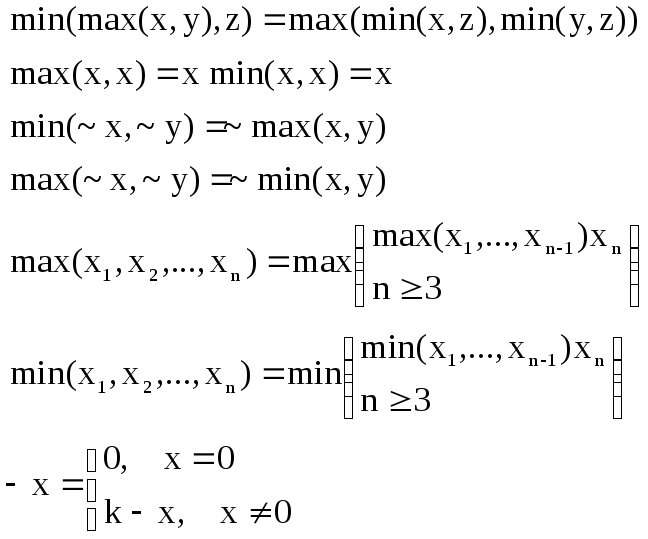
З.Ы.: Надеюсь, моя деятельность кому-нибудь помогла.