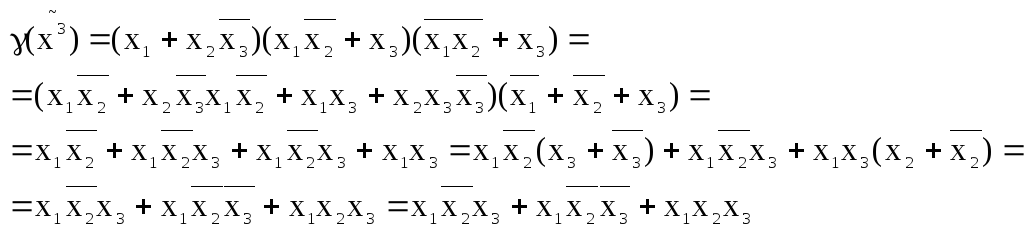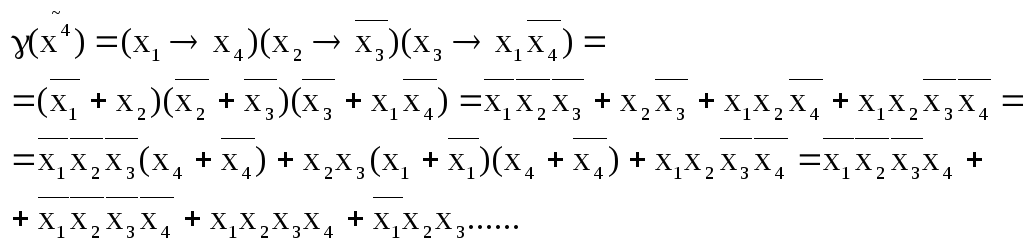LECT15
.DOCЛекция №15
Разложение булевых функций по переменным.
Возникают вопросы:
1) всякая ли функция может быть записана с помощью формулы?
2) как это сделать?
Совершенная дизъюнктивная нормальная форма.
Обозначим
,
где равен либо 0,
либо 1. Тогда
.
Поскольку
,
то x=1 x=.
Теорема о разложении функции по
переменным || Каждую функцию Булевой
алгебры
при любом
можно
представить в следующей форме:
,
где дизъюнкция берется по всем наборам
значений переменных
.
||
опр || Это представление называется разложением функции по m переменным x1,…xm.||
Доказательство.
-
Рассмотрим произвольный набор значений
.
Левая часть равенства имеет вид
.
Правая часть
(в сумме только одно произведение отлично
от нуля: то в котором
)
.
Теорема доказана.
Разложение по одной переменной
1)
Разложение по всем n переменным
2)
При
Опр. Это разложение называется совершенной дизъюнктивной нормальной формой.
Теорема || Каждая функция алгебры логики может быть выражена в виде формулы, содержащей только отрицание, конъюнкцию и дизъюнкцию. ||
Доказательство ||
1) Если
,
то
2
)
Если
,
то
Примеры
-
x1
x2
f
0
0
1
0
1
1
1
0
0
1
1
1
(это СДНФ; теперь преобразуем)
Следующий пример. Дана таблица
-
x1
x2
x3
f
0
0
0
1
0
0
1
1
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
1
1
1
0
0
1
1
1
1
П
усть
Это разложение называется совершенной конъюнктивной нормальной формой.
Примеры.
1)
2)
-
x1
x2
x3
x4
f
0
0
0
0
0
0
0
0
1
1
0
0
1
0
0
0
0
1
1
0
0
1
0
0
1
0
1
0
1
0
0
1
1
0
0
0
1
1
1
0
1
0
0
0
1
1
0
0
1
1
1
0
1
0
0
1
0
1
1
0
1
1
0
0
0
1
1
0
1
0
1
1
1
0
1
1
1
1
1
0
-
x1
x2
0
0
0
0
1
1
1
0
1
1
1
0
-
x1
x2
x3
X4
0
0
0
0
0
0
0
0
1
1
0
0
1
0
0
0
0
1
1
0
0
1
0
0
1
0
1
0
1
0
0
1
1
0
0
0
1
1
1
0
1
0
0
0
1
1
0
0
1
1
1
0
1
0
0
1
0
1
1
0
1
1
0
0
0
1
1
0
1
0
1
1
1
0
1
1
1
1
1
0
