5. Степенные ряды

Определение 16. Степенным называется ряд вида

где . (18)

Числа , , …, , … - коэффициентами степенного ряда (18).

Придавая различные числовые значения, будем получать числовые ряды, которые могут оказаться как сходящимися, так и расходящимися.

Определение 17. Множество тех значений , при которых ряд (18) сходится, называется областью сходимости степенного ряда.

Справедлива следующая:

Теорема Абеля. Если степенной ряд сходится при некотором значении , то он абсолютно сходится при всяком значении таком, что . Если ряд расходится при некотором значении , то он расходится при всяком значении таком, что (см. рис. 1).

Рис. 1

Таким образом, существует такое число (оно может быть равно 0 или ), что:

1) при ( ) ряд абсолютно сходится;

2) при ( ) ряд расходится.

Определение 18. Число называется радиусом сходимости ряда (18), если при ряд сходится, а при расходится. Интервал в этом случае носит название интервала сходимости ряда (18).

Если ряд (18) сходится на всей числовой прямой, то пишут , если он сходится только при (а это будет всегда для степенного ряда вида (18)), то пишут .

При ряд (18) может либо сходиться, либо расходиться. Этот вопрос решается отдельно для каждого степенного ряда.

Радиус сходимости степенного ряда определяется по формулам:

, ,

если соответствующие пределы существуют.

Примеры. Исследуем сходимость рядов

1)

Это степенной ряд. Все его коэффициенты, за исключением отличны от нуля. Найдём радиус и интервал сходимости данного ряда. Здесь , , поэтому удобно использовать вторую формулу для вычисления радиуса сходимости ряда:

.

Следовательно, радиус сходимости и ряд сходится на интервале .

Исследуем поведение ряда на концах интервала, то есть в точках .

При получаем гармонический ряд , который расходится.

При - ряд , который является знакочередующимся и сходится в силу признака Лейбница.

Таким образом, данный ряд сходится в любой точке полуинтервала и расходится вне него.

2) .

Это степенной ряд. Все его коэффициенты, за исключением отличны от нуля. Найдём радиус и интервал сходимости данного ряда. Здесь . Удобно использовать первую формулу для вычисления радиуса сходимости ряда:

.

Следовательно, ряд сходится в единственной точке , расходится при .

При из исходного получаем ряд , сумма которого равна 0.

5.1. Свойства степенных рядов

1. Сумма степенного ряда есть непрерывная на отрезке , где , функция.

2. Степенной ряд можно почленно интегрировать на любом отрезке , , и почленно дифференцировать в интервале .

5.2. Разложение функций в степенные ряды

Если функция имеет производные любого порядка в окрестности точки , то её можно разложить в степенной ряд

,

который называется рядом Тейлора.

Положим , тогда получим частный случай ряда Тейлора, который называют рядом Маклорена:

Пример. Разложим в ряд Маклорена функцию .

Найдём производные функции : , , , …, , .

Вычислим значения функции и производных в точке : , , , …, , .

Таким образом,

Так как , то ряд сходится на всей числовой прямой.

При разложении функций в степенные ряды используются разложения в ряд Маклорена следующих функций:

1. , ,

2. , ,

3. , ,

4. , ,

5.

, - биномиальный ряд.

Примеры. Разложим в ряд Маклорена следующие функции:

1) .

Воспользуемся разложением , .

Заменяя на , получим

, ;

, ;

, .

2) .

Воспользуемся разложением , .

Заменяя на , получим

, ,

тогда

3) - биномиальный ряд при .

Получим разложение заданной функции с помощью разложения в ряд Маклорена функции :

, .

Почленно дифференцируя данный ряд в интервале , имеем

, .

Действительно, при разложение биномиального ряда имеет такой вид.

4) .

Разложим в ряд Маклорена функцию и почленным интегрированием полученного ряда найдём разложение в ряд по степеням для функции .

Используя биномиальный ряд, напишем разложение для функции :

,

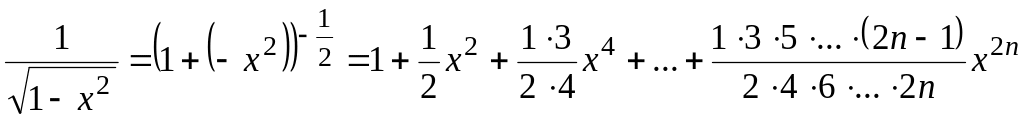тогда