Прийняття рішень у конфліктних ситуаціях

Задача 1.

Дано платіжну матрицю (табл. 1). Спростити матрицю за рахунок відбраковування явно невигідних стратегій.

Таблиця 1

Платіжна матриця

Стратегія гравців	В1	В2	В3	В4	В5
А1	8	6	4	7	7
А2	5	4	3	4	6
А3	4	3	2	3	4
А4	7	2	6	5	9

Розв’язання

У матриці (див. табл. 1, приклад 5.2) всі елементи стратегії А₁ домінують над А₂ та А₃, оскільки всі її елементи не менші від елементів стратегії А₂ та А₃ Отже, стратегії А₂ та А₃ є невигідними, порівнюючи зі стратегією А₁, і може бути відкинутими (гравець А ніколи ними не скористається). Тож, платіжну матрицю в спрощеному вигляді зображено в табл. 2.

Таблиця 2

Перетворена платіжна матриця

Стратегія гравців	В1	В2	В3	В4	В5
А1	8	6	4	7	7
А4	7	2	6	5	9

У цій матриці 1, 4 і 5 стовпці (В₁, В₄, В₅) домінують над 2 стовпцем (В₂). Оскільки, стовпці характеризують стратегії гравці В, що прагне зменшити виграш гравця В, то ці стратегії свідомо йому не вигідні. Після їхнього виключення одержуємо матрицю:

Стратегія гравців	В2	В3
А1	6	4
А4	2	6

у якій немає домінуючих стратегій.

Визначимо нижню і верхню ціни гри, одержимо:

; , звідки

Аналогічно:

; , звідки

Оскільки, , то ця гра не має сідлової точки і розв’язком її буде змішана стратегія.

Задача 2.

Знайти сідлову точку в грі, що характеризується платіжною матрицею, даною в табл. 2.

Таблиця 2

Платіжна матриця

Стратегії гравців	В1	В2	В3	В4	В5
А1	– 50	10	10	30	– 50
А2	40	20	– 50	– 60	– 20
А3	50	30	40	60	40
А4	70	– 30	30	– 10	– 60

Розв’язання

α = max(– 50; – 60; 30; – 60) = 30; β = (70; 30; 40; 60; 40) = 30; 30 = 30.

Висновок: точка на перетині стратегій А₃ і В₂ є сідловою точкою.

Оптимізація структури портфеля цінних паперів

Задача 1.

Два цінних папери, позначені індексами 1 та 2 відповідно, мають очікувані ефективності = 10 % і = 12 % та ступінь ризику = 2,3 % і = 2,8 %. Коефіцієнт кореляції (міра взаємодії цінних паперів на ринку) = 0,3.

Допустимо, частка паперу першого виду в портфелі = 0,6. Тоді = 1-0,6=0,4. Розрахуємо середню норму прибутку та ризик портфеля, сформованого з цих паперів.

Середня ефективність портфеля із двох цінних паперів:

Ризик портфеля із двох цінних паперів (дисперсія):

Цей приклад показує, що ризик портфеля є менший, аніж ризик кожного з паперів, які входять до його складу, а середня ефективність більша від меншої і менша від більшої з середніх ефективностей окремих цінних паперів, тобто:

і ;

Чи може цей портфель мати кращі характеристики?

Знайдемо оптимальні частки за відповідними співвідношеннями і отримаємо:

Середня ефективність портфеля:

Середній ризик (дисперсія) оптимального портфеля цінних паперів:

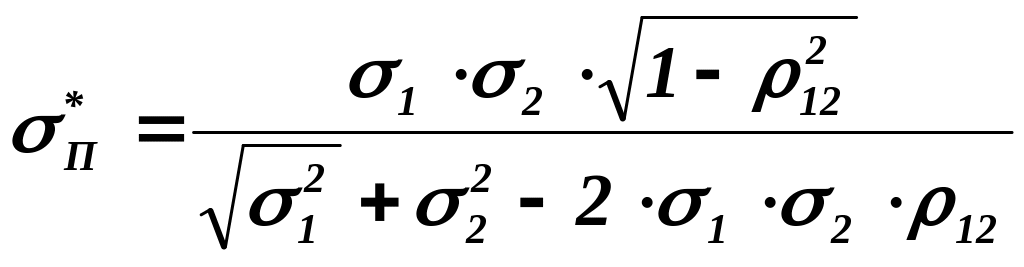
Отже, поєднання оптимальних часток двох цінних паперів у портфелі забезпечує менше значення ризику порівняно із поєднанням допустимих часток ( на 0,01% (2,02 менше 2,01); разом з тим і середня ефективність портфеля зменшилася з 10,8 % до 10,74 %.

Задача 2.

Нехай інвестор володіє портфелем цінних паперів з характеристиками = 30 %, = 5 %. На ринку доступні державні облігації, норма прибутку яких фіксована, тобто = 10 %. Як буде змінюватися норма прибутку портфеля при зміні значень ризику?

Норма прибутку портфеля цінних паперів:

Коефіцієнт показує, наскільки зміниться норма прибутку портфеля, якщо ризик зміниться на 1 %.

Тобто для ефективних портфелів кожний додатковий відсоток ризику вимагає збільшення початкового значення норми прибутку (див. табл.)

Ризик портфеля, , %	Ефективність портфеля, , %
0	10
2	18
5	30
10	50
12	58

9