7.Построение графика переходного процесса по вчх.

Построим ВЧХ замкнутой системы:

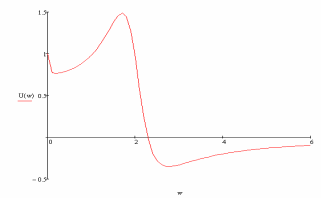
Рисунок 30. ВЧХ замкнутой системы.

Рассмотрим разработанную В. В. Солодовниковым методику построения графика переходного процесса по ВЧХ. Для этого заменим ее ломаной линией и представим алгебраической суммой нескольких трапеций:

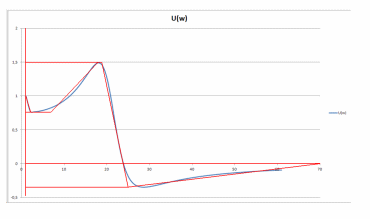
Рисунок 31. Замена ВЧХ ломаной линией.

Рисунок 32. Замена ВЧХ на трапеции.

Определим параметры нормированных трапеций:

Рисунок 33. Нормированная трапеция.

Трапеция I				Трапеция II
r0	wd	w0	X	r0	wd	w0	X
0,23	0	2	0	-0,73	8	16	0,5
tт	hт	t	h(t)	tт	hт	t	h(t)

Трапеция III				Трапеция IV
r0	wd	w0	X	r0	wd	w0	X
1,83	21	25	0,84	-0,33	25	70	0,357143
tт	hт	t	h(t)	tт	hт	t	h(t)

По полученным данным найдем величину переходной характеристики и время для каждой трапеции и построим графики переходных процессов (данные по трапециям приведены в приложении А). Чтобы получить график переходного процесса для замкнутой системы необходимо алгебраически сложить графики всех трапеций.

Рисунок 34. График переходного процесса.

8.Оценка качества сау.

Исходя из рисунка 35 время регулирования(tрег) составило 1,5 секунды.

Рисунок 35. Время регулирования.

9.Улучшение показателей качества. Определение передаточной функции корректирующего устройства.

Необходимо улучшить показатели качества нашей системы в 2 раза (уменьшить время регулирования с 1,5 до 0,75 секунд). Для этого нужно добавить в систему корректирующее устройство.

Определим передаточную функцию корректирующего устройства по ЛАЧХ разомкнутой системы (рис. 36):

Рисунок 36. Построение ЛАЧХ корректирующего устройства.

Передаточная функция для корректирующего устройства будет выглядеть так:

где Т1, Т2, Т3, Т4 и Т5 параметры времени, найденные из ЛАЧХ корректирующего устройства (рис. 36).

T1=0,7; T2=0,2; T3=0,03; T4=0,01; T5=0,000769

Построим график переходного процесса для системы с корректирующим устройством методом трапеций.

Найдем передаточную функцию системы с корректирующим устройством:

Разделим передаточную функцию разомкнутой системы на вещественную(А) и мнимую(В) части числителя и вещественную(С) и мнимую(D) части знаменателя. Выпишем их:

Построим ВЧХ:

Рисунок 37. Построение ВЧХ.

Рисунок 38. Замена ВЧХ ломаной линией.

Рисунок 39. Замена ВЧХ на трапеции.

Определим параметры нормированных трапеций (данные по трапециям приведены в приложении Б).

Построим графики трапеций и переходного процесса:

Рисунок 40. График переходного процесса