
- •Задание № 1 Построение эпюр внутренних силовых факторов и расчёт на прочность и жёсткость при центральном растяжении-сжатии
- •Пояснения к подготовке построения эпюры нормальной силы
- •Определение значения опорной реакции r
- •Построение эпюры нормальной силы
- •Условие прочности
- •Эпюра перемещений поперечных сечений стержня
Построение эпюры нормальной силы
Для
построения эпюры на первом участке при
0≤x1≤а
в соответствии с методом сечений мысленно
рассечём стержень на произвольном
расстоянии x1
от левого конца и отбросим правую его
часть. Рассмотрим равновесие оставшейся
части стержня. По
правилу сечений
нормальная сила в этом сечении равна
сумме проекций на ось x всех внешних
сил, действующих слева от рассматриваемого
сечения:
 .
.
Отрицательное значение нормальной силы на этом участке означает, что этот участок находится в условиях сжатия. Подставим предельные значения интервала для x1: при x1 = 0 нормальная сила Nx1 = -R = -30 кН, при x1= а значение этой силы Nx1 = -R - q1*a= -30 - 10*0.2 = =-32 кН. Это показано на эпюре.
На
втором участке при a≤x2≤(b+c)
нормальная сила равна
 ,
т.е. Nx2=-R
- q1*a
+ P1=
-30-10*0.2+16=-16 кН. На этом участке действует
сжимающая нормальная сила Nx2=-16
кН. Она имеет постоянное значение, т.к.
в уравнении для Nx2
нет переменной x2.
,
т.е. Nx2=-R
- q1*a
+ P1=
-30-10*0.2+16=-16 кН. На этом участке действует
сжимающая нормальная сила Nx2=-16
кН. Она имеет постоянное значение, т.к.
в уравнении для Nx2
нет переменной x2.
Сила P3, приложенная к правому торцу стержня, замыкает эпюру: -16+16=0.
Примечание. Если внешняя сила совпадает с осью, на которую она проектируется, или параллельна этой оси, то проекция равна самой силе, т.е. совпадает с ней по величине. Если внешняя сила P отклоняется от оси x на угол α, то проекция Xi = P*cosα.
Единица силы в системе СИ называется ньютоном (Н). Эта сила сообщает телу массой 1 кг ускорение 1 м/с2. 1 Н = 0,102 кгс. Единица названа по имени английского учёного Исаака Ньютона (1643-1727), создателя классической механики, дифференциального и интегрального исчисления. В задачах Сопротивления материалов применяется единица в тысячу раз большая – килоньютон (кН): 1 кН = 103 Н.
Распределенная нагрузка по длине стержня имеет размерность кН/м. 1 кН/м = 103 Н/103 мм= 1 Н/мм.
Единица давления и механического напряжения в системе СИ названа паскалем (Па) по имени французского учёного Блеза Паскаля (1623-1662), основоположника гидростатики. 1 Па = 1 Н/м2. В практических расчётах применяется единица в миллион раз большая – мегапаскаль (МПа): 1 МПа = 106 Н/м2 = 106 Н/106 мм2 = 1 Н/мм2.
Условие прочности
Для построения эпюры напряжений необходимо определить размеры поперечного сечения стержня. Так как заданный стержень круглого поперечного сечения, то следует определить диаметр стержня, который выдержит заданные нагрузки. Для этого ведется расчёт по допускаемым напряжениям. Суть этого расчёта заключается в том, что максимальные напряжения, возникающие в опасном сечении стержня, не должны превышать допускаемого напряжения для материала, из которого изготовлен стержень. При центральном растяжении или сжатии, при котором внешние силы направлены по оси стержня, в поперечных его сечениях возникают нормальные напряжения σ, которые равномерно распределены по сечению и равны σ = N/F, где F – площадь поперечного сечения. Судя по эпюре, наибольшие по абсолютной величине нормальные силы возникают на границе между участками a и b. Эти силы равны по модулю [Nmax] = 32 кН.
Для растяжения или сжатия условие прочности имеет вид:
 212\* MERGEFORMAT (.)
212\* MERGEFORMAT (.)
где
 – допускаемое напряжение, оно задано
для материала стержня из стали ([
]
= 160 МПа). Если
формулу (1.1) решить относительно площади
поперечного сечения стержня F,
то получим:
– допускаемое напряжение, оно задано
для материала стержня из стали ([
]
= 160 МПа). Если
формулу (1.1) решить относительно площади
поперечного сечения стержня F,
то получим:
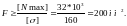
В эту формулу значение силы подставлено в Н, а напряжения в МПа, т.к. 1 МПа = 1 Н/мм2, то площадь сечения стержня выражена в мм2.
Для
круглого сечения
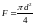 ,
отсюда диаметр стержня равен
,
отсюда диаметр стержня равен
 .
Результат округляем до d
= 16 мм.
.
Результат округляем до d
= 16 мм.
Эпюра нормальных напряжений
При построении эпюры нормальных напряжений используется формула σ = N/F, т.к. стержень имеет одну и ту же площадь поперечного сечения F = 200 мм2 = const, то эпюра будет подобна эпюре N.
На
первом участке (0≤x1≤а)
при x1
= 0 нормальная сила N1
= -30 кН и нормальное напряжение
 ,
при x
= a
сила N1
= -32 кН и напряжение
,
при x
= a
сила N1
= -32 кН и напряжение
 .
.
На
втором участке при a≤x2≤(b+c)
нормальная сила N2
= -16 кН и напряжение
 =const.
=const.
Эпюра относительных деформаций
Для построения эпюры относительных деформаций ε используется закон Гука, который отражает прямую пропорциональную зависимость между напряжением и деформацией, возникающих в конструкции под нагрузкой:
 ,
(1.2)
,
(1.2)
где
E
– модуль упругости первого рода, для
стали Е=2*105
МПа; ε – относительная деформация,
которая определяется по формуле
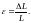 В этой формуле L
– длина стержня, а ΔL
– абсолютное удлинение (укорочение)
стержня при растяжении (или сжатии). Для
вычисления деформации формула закона
Гука преобразуется к виду:
В этой формуле L
– длина стержня, а ΔL
– абсолютное удлинение (укорочение)
стержня при растяжении (или сжатии). Для
вычисления деформации формула закона
Гука преобразуется к виду:
 .
Эпюра деформаций подобна эпюре нормальных
напряжений, т.к. модуль упругости Е =
const.
.
Эпюра деформаций подобна эпюре нормальных
напряжений, т.к. модуль упругости Е =
const.
При
x1
= 0 нормальное напряжение σ = -150 МПа, а
деформация
 .
При x1
= а напряжение σ = -160 МПа, деформация
.
При x1
= а напряжение σ = -160 МПа, деформация
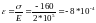 .
На втором участке при a≤x2≤(b+c)
нормальное напряжение σ = -80 МПа и
деформация
.
На втором участке при a≤x2≤(b+c)
нормальное напряжение σ = -80 МПа и
деформация
 .
.
