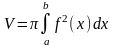Розв'язання

Область визначення даної функції — R.

Знайдемо f`(x): f`(x) = (x³ - 3x)' =3х²- 3.

Похідна існує для всіх x є R.

Знайдемо стаціонарні точки: f(x) = 0, 3х² - 3 = 0, х² — 1 = 0, x = ±1.

Наносимо область визначення та стаціонарні точки на коор­динатну пряму (рис. 48) і визна­чимо знак похідної на кожному проміжку:

f `(-2) = 3 · (-2)² - 3 = 9 > 0;

f`(0) = 3 · (0)² - 3 = -3 < 0;

f`(2) = 3 · (2)² - 3 = 9 > 0.

Точка χ = -1 є точкою максимуму, бо похідна при переході через цю точку змінює знак з «+» на «-»: х_max = -1.

Точка х = 1 — є точкою мінімуму, бо похідна при переході через цю точку змінює знак з «-» на «+»: х_min = 1.

Відповідь: х_max= -1, х_min= 1.

знаходження найбільшого і найменшого значень функції на відрізку [а; b] треба:

1) Знайти значення функції на кінцях проміжку, тобто числа f(a) і f(b);

2) Знайти значення функції в тих стаціонарних точках, які на­лежать інтервалу (а; b);

3) Із знайдених значень вибрати найбільше і найменше.

Приклад 1. Знайдіть найбільше і найменше значення функції f(x) = x + e^-x на відрізку [-1; 2].

Розв'язання

Знайдемо значення функції в точках x = -1 та x = 2:

f(-1) = -1 + e^l = e – l, f(2) = 2 – е ^-2 = 2 – .

Знайдемо f’(x): f'(x) = (x + е^-x)¹ = 1 - е^-x. Знайдемо стаціонарні точки:

f'(x) = 0; 1 - е^-x = 0; 1 - = 0; е^x = 1; x = 0.

Знайдемо значення функції в точці x = 0: f(0) = 0 +е°= 1.

І з чисел е - 1 1,72, 2 - 1,86 та 1 найбільшим є 2 - , а найменшим -1.

Відповідь: f_найб. = f(2) =2 - ; f_найм. = f(0) = 1.

Дослідження функції і побудову її графіка будемо виконува­ти за таким планом:

1. Знаходимо область визначення функції.

2. Знаходимо точки перетину графіка з координатними осями.

3. З'ясовуємо парність (непарність), періодичність функції.

4. Знаходимо похідну та стаціонарні точки.

5. Знаходимо проміжки зростання, спадання, точки екстремуму та екстремальні значення функції.

6. З'ясовуємо поведінку функції на кінцях області визначення.

7. На підставі проведеного дослідження будуємо графік функції.

ІНТЕГРАЛ

Функція F(x) називається первісною функції f(x) на деякому про­міжку, якщо для всіх x із цього проміжку виконується рівність: F'(X) = f(x).

Теорема 1. Нехай функція F(x) є первісною для f(х) на деякому проміжку. Тоді для довільної постійної С функція F(x) + С також є первісною для функції f(х).

Теорема 2. Нехай функція F(x) є первісною для f(x) на деякому проміжку. Тоді будь-яка первісна для функції f(x) на цьому проміжку може бути записана у вигляді F(x) + С, де С — деяка стала (число).

Сукупність усіх первісних для функції f(x) на проміжку називають невизначеним інтегралом цієї функції і позначають 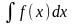. функцію f(x) називають підінтегральною функцією.

З доведених теорем випливає, що = F{x) + С, де F(x) — яка-небудь первісна для функції f(x) на даному проміжку, С — довільна стала (її називають сталою інтегрування).

Таблиця первісних (невизначених інтегралів)

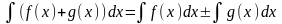
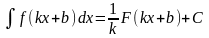
формула Ньютона-Лейбніца набирає вигляду:

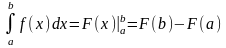
Із властивостей первісної і формули Ньютона-Лейбніца ви­пливають основні властивості інтеграла.

1. Інтеграл суми (різниці) функцій дорівнює сумі (різниці) інтегралів :

.

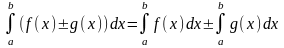2) Постійний множник можна виносити за знак інтеграла:

3) Якщо с є [а; b], то