4. Преобразования Фурье и Лапласа

Режимы работы разнообразных электротехнических и электронных устройств связаны с несинусоидальными токами и напряжениями. Детерминированные сигналы в разнообразных АСУ также могут быть периодическими или непериодическими.

При анализе подобных систем помимо временного "языка", т.е. описания во временной области, где аргументом функций служит время, широко используется "частотный язык , т.е. описание в частот­ной области, где аргументом функций служит частота. Взаимосвязь и переход от одной формы описания сигналов к другой дают пре­образования Фурье и Лапласа.

В качестве примера представим некоторую линейную цепь (рис.8) из ряда идеальных источников напряжения, не влияющих друг на друга. В силу принципа суперпозиции напряжение u(t) на нагрузке Z _нагр будет складываться из напряжений источников, т.е.

Пусть, помимо источника постоянного напряжения U₀ , остальные источники гармонические, тогда

Если то напряжения на нагрузке при бесконечном числе источников бу­дет выражаться рядом Фурье в тригонометрической форме:

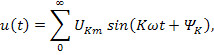
называют основной частотой, a -ее гармоника­ми. Отбросив члены ряда после n-го, получим аппроксима­цию периодической функции u(t) , подчиняющейся условиям Дирих­ле, в виде тригонометрического полинома

Здесь коэффициенты ряда Фурье определяют следующим образом: постоянная составляющая представляет собой среднее значение за период амплитуды синусоидальных составляющих ряда

амплитуды косинусоидальних составляющих ряда

амплитуды гармоник ряда (13 ) и их фазы находятся по формулам

Таким образом, с помощью ряда Фурье периодическую функцию времени можно представить в виде набора гармоник с частотами амплитудами и фазами

Совокупность амплитуд - называют амплитудным спектром, а фаз - фазовым спектром функции u(t)

Спектральное (частотное) и временное представления в случае приведенного примера , когда

при различных фазах и представлены на рис.9: на рис.9 а временное представление, рис.9 б, в – спектральное.

Из приведенного примера видно, что действие совокупности источников можно заменить эквивалентным источником напряжения сложной формы (негармонического сигнала) и, что особенно важ­но, наоборот, действие такого источника можно представить сово­купностью гармонических источников (источник частоты -есть источник постоянного напряжения).

Замечательная особенность преобразования Фурье заключается в том, что совокупность амплитудного и фазового спектров позво­ляет восстановить форму сигнала во времени и, наоборот, по фор­ме сигнала можно найти спектры амплитуд и фаз.

При наличии симметрии в кривой напряжения (тока), выраженных функциями времени, в ряде Фурье будут наблюдаться особен­ности. Например, для кривой u(t) , показанной на рис.5, в силу симметрии относительно оси абсцисс и начала координат от­сутствуют: постоянная составляющаяся сигнала и косинусоидаль­ные составляющие, т.е. i

где

Формулы (16) и (17) представляют собой пару преобразований Фурье для непериодических функций, они связывают вещественную функ­цию времени и комплексную функцию частоты . Фopмула (16) называется интегралом Фурье. Ее физический смысл заклю­чается в том, что непериодическая функция состоит из суммы си­нусоид с непрерывной последовательностью частот.

Анализ поведения электрической цепи в частотной области требует знания не только спектральных характеристик сигнала, но и частотных характеристик электрических цепей.

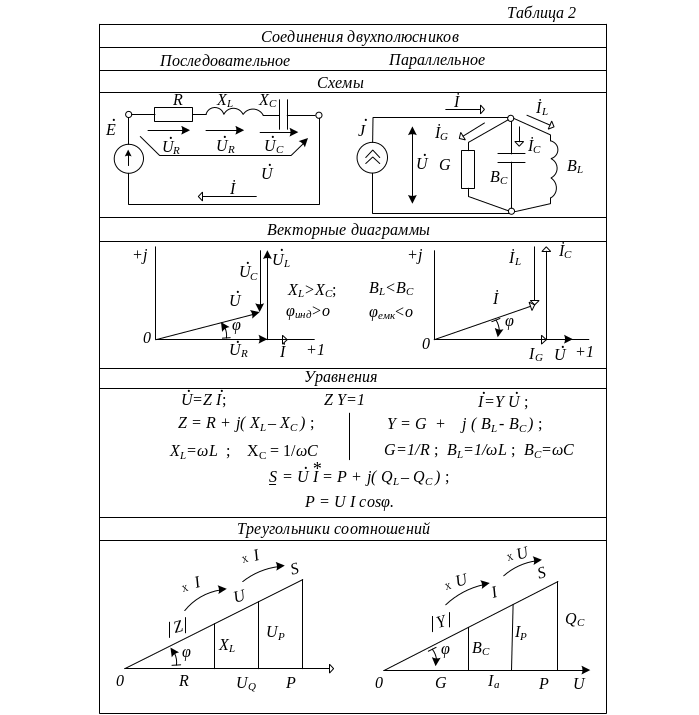
Частотные характеристики сопротивлений; или проводимостей двухполюсников, образующих цепь, предопределяют частотные, в том числе и резонансные свойства цепи в целом. Характерные особен­ности удобно проследить на пассивных реактивных двухполюсниках.

Одноэлементными реактивными двухполюсниками являются индук­тивный и емкостной. Знак сопротивления и проводимости для них не зависит от частоты, в отличие от неоднородных двухполюсников, содержащих L и С в разных сочетаниях. Характер зависимостей сопротивлений и проводимостей рассматриваемых элементов показан на рис.10, из которого видно, что как сопротивления, так и про­водимости (с учетом знака) растут с повышением частоты, т.е.

Это свойство (18 ) сохраняется для любых реактивных двухполюсни­ков и носит название теоремы Фостера.

Для двухэлементных реактивных двухполюсников возможны два соединения: последовательное и параллельное, показанные на рис.11. Графики суммарных входных сопротивлений и проводимостей можно получить координатным сложением характеристик отдельных составляющих элементов.

Нетривиальные нули функций и соответствуют резонансам напряжений и тока соответственно. Значения частоты, в которых или называют полюсами и отмечают их на графике крестиками (рис.11 6,г). Сопоставление графиков на рис.10, II а, б и рис.11 в, г лишний раз показывает дуальность L и С элементов.

В многоэлементном двухполюснике (рис.12 а) частотная харак­теристика по теореме Фостера имеет чередующиеся нули и поло­сы, т.е. резонансы напряжений и тока следуют друг за другом (рис.12 б).

Если однородные элементы (или группы элементов) с одинако­выми резонансными частотами, соединенные параллельно или после­довательно, заменить одним эквивалентным элементом, то для тако­го "приведенного" двухполюсника сумма чисел полюсов и нулей (не считая точек и ) будет на единицу меньше числа элементов.

В общем случае частотная характеристика при начинается с 0, если между зажимами есть путь для постоянного тока и из -в противоположном случае, в котором первым наступит резонанс напряжений (рис.12 б).

Отмеченные особенности позволяют по принципиальной схеме двухполюсника качественно (а при необходимости и количественно) исследовать частотные характеристики цепи.

В общем случае характеристики элементов цепей (или звень­ев систем автоматического управления) определяют их реакцию на гармонически изменяющийся входной сигнал. Частотная характерис­тика определяется как передаточная функция при , т.е.

Здесь - амплитудно-частотная характерис­тика, а - фазочастотная характерис­тика. Модуль частотной характеристики реальных систем в зависимости от изменяется в очень широких пределах от 0 до 10⁶ . Поэтому частотные характеристики изображают в логарифмической масштабе.

Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) определяется соотношением

и измеряется в децибелах (дБ).

Логарифмическая фазочастотная характеристика (ЛФЧХ) измеряется в радианах или градусах.

Для изображения и применяется полулогариф­мическая система координат: по оси абсцисс откладывается в логарифмическом масштабе, а по оси ординат -в децибелах и в градусах или радианах ( рис. 13). Изменение в два раза соответствует октаве, а в десять раз - декаде. Например, интервалу частот от 1 до 8 Гц соответствуют 3 октавы, а интерва­лу 0,1 до 1000 Гц - 4 декады.

Удобство использования логарифмического масштаба заключает­ся в том, что ЛАЧХ обычно аппроксимируются отрезками прямых ли­ний - асимптотами, упрощающими их построение, наклон асимптот выражают в децибелах на декаду или децибелах на октаву.

В качестве примера рассмотрим передаточную функцию вида

ее ЛАЧХ найдем по формуле ( 20 )

при

Следовательно наклон ЛАЧХ составит т. е. минус двадцать децибел на декаду (рис.13).

Преобразование Фурье применимо только для сигналов абсо­лютно интегрируемых в бесконечных пределах. Поэтому такие широ­ко используемые сигналы как ступенчатая или синусоидальная функции, неограниченно нарастающие по времени, не могут рассматри­ваться с помощью преобразований Фурье.

Если в прямом преобразовании Фурье (16) заменить перемен­ную комплексной частотой , то у функции време­ни под знаком интеграла появится множитель вносящий затухание при соответствующем значении Это обеспечит абсолютную интегрируемость при . В результате получаем преобразование Лапласа (одностороннее) вида

Интеграл (20) сходится и преобразование Лапласа существует для функций времени, тождественно равных нулю при , а при являющихся однозначными кусочно- непрерывными с конеч­ным числом конечных разрывов, причем при

функции ограни­чены в росте экспонентой , где - абсцисса абсолютной сходимости.

С помощью интеграла Лапласа ( 20) - прямого преобразова­ния, заданная функция вещественной переменной ( оригинал) преобразуется в функцию комплексной переменной (комплексной частоты), называемую изображением оригинала.

Значение (оригинала F (Р)) по заданному лапласовому изображению F(P) определяется с помощью обратного преоб­разования Лапласа

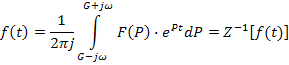
Обратное преобразование Лапласа позволяет представить исследуемую функцию в виде суммы бесконечно большого чис­ла малых членов, каждый из которых представляет колебание с бесконечно малой" амплитудой, затухающей по экспоненциальному закону (сравните с преобразованием Фурье, где амплитуды гар­моник были постоянными). Вопросы, связанные с интегрированием в плоскости комплексного переменного, и свойства преобразования Лапласа подробно изучаются в разделе курса математики Теория функций комплексного переменного, называемом операционным ис­числением.

Следует иметь в виду, что в научно-технической литерату­ре отсутствует единообразие в обозначении комплексной перемен­ной (S и Р) и преобразования Лапласа ( и т.д.). Электрические свойства цепей можно характеризовать функциями, представляющими собой отношение лапласовых преоб­разований реакции цепи (ее выходной переменной) и возбуждаю­щего цепь воздействия (входной переменной). Такие отношения в теории электрических цепей называют системными функциями цепей, а в теории автоматического управления - передаточными функциями.

Если, например, - воздействие, - реакция линейной цепи на него, то передаточная функция равна отноше­нию их лапласовых изображений

При этом начальные запасы энергии в цепи полагают равными ну­лю (нулевые начальные условия).

Операторный метод используют для анализа переходных процессов, которые возникают в цепи при коммутациях или изменении параметров цепи. После коммутации происходит нестационар­ный переход, системы в новое установившееся состояние.

В операторном методе интегро-дифференциальные уравнения послекоммутационной схемы приводят к алгебраическим уравнениям в изображениях, используя преобразование Лапласа, при этом учи­тывают начальные условия. Решение системы алгебраических урав­нений дает изображение искомой функции, оригинал которой может быть получен путем использования обратного преобразования Лапласа.

Операторная форма уравнений основных элементов цепей выра­жается следующим образом.

Для активного сопротивления и , используя метод преобразований Лапласа, находим

откуда операторное сопротивление и проводимость равны

Для индуктивного элемента ток в момент коммутации равен (рис.14,а). Найдем лапласово изображение напряжения на зажимах катушки L .В соответствии о теоремой дифференцирования оригинала

или

где

Уравнение ( 21 ) можно трактовать как уравнение последовательного соединения индуктивного элемента с нулевым начальным током и идеального источника напряжения U (рис.14.б). От последовательной схемы замещения можно перейти к эквивалент­ной параллельной (рис.14,в), в которой ток источника

откуда ток

Аналогично емкостной элемент С (рис. 14 г) с начальным напряжением U(0) можно представить в виде незаряженной емкости С и идеального источника тока J (рис. 14 д) или напряжения U (рис. 14 е). В соответствии с теоремой дифференцирования оригинала

и

где

и

Введенные идеальные источники, учитывающие начальные условия, называют источниками, эквивалентными начальным условиям; число таких источников должно быть равно числу тех реактивных элементов исходной схемы, для которых отличны от нуля начальные условия. Выбор типа источников напряжения или тока определяется удобствами расчетов.

Таким образом, при нулевых начальных условиях параметры электрической цепи в операторной форме выражаются формулами, приведенными в табл.3.

Таблица 3

Элемент	Параметры
	Сопротивление	Проводимость
Резистивный
Индуктивный
Емкостной

Законы Кирхгофа в оперативной форме примут вид:

т.е. сумма изображений токов в узле и сумма изображений напряжений в контуре равны нулю. В эти суммы должны входить также изображения эквивалентных источников начальных условий.

П. АНАЛИЗ СЛОЖНЫХ ЦЕПЕЙ