МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНЖЕНЕРНОЙ ЭКОЛОГИИ

(МОСКОВСКИЙ ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ ИНСТИТУТ ХИМИЧЕСКОГОМАШНОСТРОЕНИЯ)

Г.А.Кардашев

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ АВТОМАТИКИ

Учебное пособие

Допущено редакционно-издательским советом

-

Москва – 2009

УДК 62 - 52

Г.А.Кардашев

Электрические цепи и сигналы автоматики: Учебное пособие.

М.: ШМ, 2009, 51с.

В учебном пособий изложены основы теории линейных электри­ческих цепей применительно к системам электроавтоматики. Рас­смотрены двухполюсные и четырехполюсные элементы цепей, топо­логия электрических схем и анализ электрических сигналов. Боль­шое внимание уделено современным матрично-топологическим мето­дам анализа электрических цепей, частотным характеристикам, ис­следованию систем с помощью сигнальных графов и электрическому моделированию. Пособие дает введение в САПР и машинный анализ электрических цепей. Предназначено для студентов, обучающихся по специальности 0639 "Автоматизация и комплексная механизация химико-технологических процессов".

Рис.31. Табл.5. Библиогр. 6 назв.

Рецензенты:

Кафедра электротехники и электроники Московского химико-технологичоского института им. Д.И.Менделеева. Е.С.Филатов, Московский Филиал Всесоюзного научно-исследовательского института химической промышленности.

ВВЕДЕНИЕ

Современные электротехнические и электронные устройства и системы автоматизации и комплексной механизации в химической промышленности представляют собой технические объекты - слож­ные системы, состоящие из большого количества взаимодействую­щих элементов. В настоящее время для анализа и разработки по­добных объектов широко используются системы автоматизированно­го проектирования (САПР), основанные на блочно-иерархическом подходе к сложным системам, заключающемся в расчленении процес­са проектирования и представления о самом объекте на уровни.

На нижнем уровне (микроуровне) при моделировании исполь­зуется функции нескольких независимых переменных (пространственных координат и времени), рассматриваемые как непрерывные. В задачах электротехники и электроники это векторы плотности электрического тока, напряженности электрического поля и дру­гие величины теории поля. Математические модели объектов данно­го уровня представляют собой дифференциальные уравнения в част­ных производных. Математические модели данного уровня являются распределенными (в пространстве) моделями. На микроуровне про­водится моделирование собственно базовых элементов систем (ре­зисторов, конденсаторов, транзисторов, интегральных микросхем и т.д.).

Интегрирование уравнений моделей микроуровня по координа­там приводит к математическим моделям с сосредоточенными постоян­ными или к макроуровню (среднему уровню иерархии). Независимой переменной в моделях макроуровня выступает время. Элементами этого уровня являются объекты, которые на микроуровне рассматри­вались как системы (резисторы, транзисторы, трансформаторы, ре­ле и т.п.) Модели среднего уровня предстаяляют набор дискрет­ных элементов, описываемых интегральными характеристиками. При­менительно к электротехнике, электронике и электроавтоматике основной теорией, описывающей поведение систем на этом уровне, является теория электрических цепей.

Переменными, которые описывают состояние отдельных блоков (элементов) цепей, являются ток i(t) и напряжение U(t), как функции времени. Теория электрических цепей, как частный случай, включает в себя теорию электронных цепей (т.е. цепей промышленной электроники, содержащих полупроводниковые, транзисторные и т.п. элементы), а также позволяет с использованием метода аналогии описать цепи другой физической природы (механические, гидравли­ческие, тепловые, магнитные и др.) и, цепи смешанные (например, пневмоэлектрические). Последнее особенно важно при анализе и проектировании систем электроавтоматики. Математические модели систем на макроуровне представляют собой обыкновенные дифференциальные уравнения в частных случаях статических задач превращающиеся в алгебраические и трансцендентные уравнения.

Дальнейшая интеграция элементов макроуровня приводит к сле­дующему (высшему) иерархическому уровню, называемому информаци­онным. Системы этого уровня - сложные устройства и комплексы ти­па вычислительных машин и автоматизированных систем управления технологическими процессами (АСУ ТП).

Процесс проектирования также разбивается на уровни различ­ного функционального содержания: структурный, функционально-ло­гический, схемотехнический, конструкторский и т.д. Для каждого уровня разрабатываются соответствующие математические, програм­мные, информационные, лингвистические и технические средства САПР.

В данном пособии отражаются лишь некоторые (вводные) поня­тия, относящиеся к автоматизации схемотехнического проектирова­ния, в основе которого лежит машинный анализ схем.

1. OCНOBЫ АНАЛИЗА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ И СИГНАЛОВ

1. Элементарные цепи

Задача анализа электрических устройств и систем решается в несколько этапов. Вначале реальное устройство или система за­меняются дискретной совокупностью стандартных элементов, соеди­ненных между собой в электрическую цепь. Эта цепь по своим ха­рактеристикам должна в заданном диапазоне изменения переменных моделировать поведение реального устройства (или системы. За­тем цепи ставится в соответствие модель, состоящая из идеали­зированных элементов,- схема замещения цепи и проводится ана­лиз работы этой схемы. Всякая схема эквивалентна (адекватна") реальному устройству или элементу лишь со стороны внешних выво­дов.

В качестве отдельных компонентов математических моделей вы­ступают уравнения, описывающие поведение идеализированных схем­ных элементов. Полное описание системы в виде программы прово­дится на основании законов электрических цепей.

Любая программа машинного анализа схем допускает лишь определенный базовый набор схемных элементов, для которого она была разработана. Выбор базового набора определяет степень многофункциональности в решении задач данной программой. Для анализа и синтеза адекватных схемных моделей большого числа электротехнических и электронных устройств и систем, представ­ляющих интерес, минимальный базовый набор должен содержать по крайней мере шесть типов двухполосных схемных элементов, при­веденных в табл.1.

Резистивные элементы с параметрами сопротивление R и проводимость G моделируют диссипацию электромагнитной энер­гии в электрической цепи.

Индуктивный элемент и емкостной элемент о параметрами индуктивность L и емкость С моделируют накопление магнитной и электрической энергии в электрической цепи.

R, G, L, C - элементы являются пассивными, так как не преобразуют другие виды энергии в электромагнитную.

Идеальный источник напряжения с параметром э.д.с. E и идеальный источник тока с параметром задающего тока J мо­делируют активные элементы, преобразующие различные виды энергии в электромагнитную.

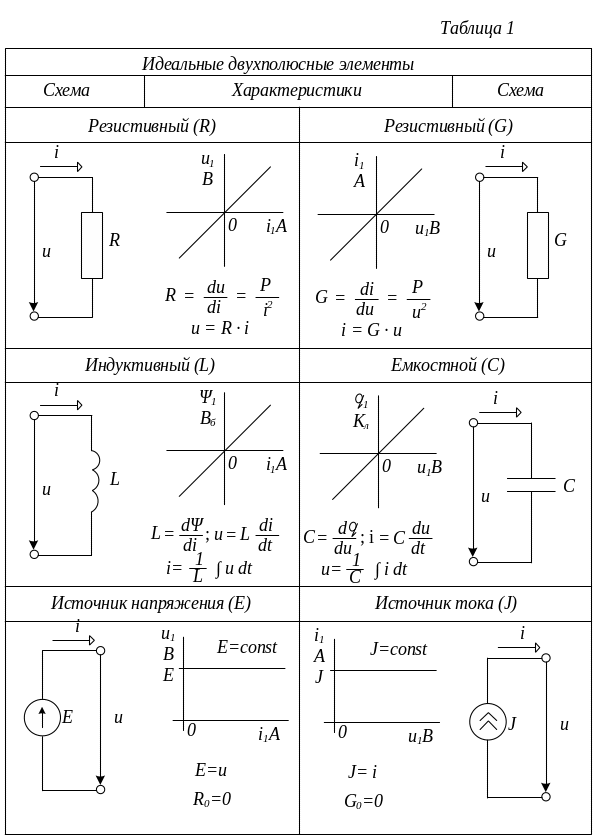
Все рассматриваемые идеальные схемные элементы являются линейными двухполюсниками, состояние которых описывается связью напряжения U(t) на их зажимах (полюсах) и током в них i(t).

Запись уравнений в табл.1 проведена в соответствии с условно-положительными направлениями на схемах. Графический характеристики элементов в табл.1 указывают на их линей­ность.

Сопоставляя уравнения элементов левой и правой колонок табл.1, можно обнаружить, что они перехотят для соответствующих элементов друг в друга при замене i↔U и смене парамет­ра. Эта. особенность называется дуальностью ( двойственностью). Таким образом, дуальны элементы R↔G , L↔С , E↔J.

Основными законами электрических цепей является два зако­на, Кирхгофа:

1-й закон Кирхгофа или закон токов

∑ik=0 (1)

и 2-й закон Кирхгофа или закон напряжений

∑Uk=0 (2)

Эти законы, как нетрудно видеть, также дуальны.

Совокупность уравнений, составленных по 1-му и 2-му за­конам Кирхгофа, дает возможность образовать систему линейно-независимых уравнений электрической цепи, решение которой оп­ределяет режим цепи. Оба закона Кирхгофа не ограничивают вида элементов с сосредоточенными параметрами (линейные, нелинейные) пассивные, активные и т.д.).

Реальные элементы цепей, как уже отмечалось, могут иметь свойства отличающиеся от отдельных идеальных схемных элементов. Однако сочетания из элементов базового набора позволяют составить более точные модели. Например, при определенных условиях реальная катушка, не содержащая магнитопровода из ферромагнитно­го материала, может быть представлена схемой замещения из после­довательного соединения L и R элементов (рис.1 a), а реальный конденсатор - параллельным соединением С и G элементов (риc.1 б).

В приведенных моделях учитываются потери в проводнике R и диэлектрике G . Реальные источники обладают конечной мощностью, что учитывается введением собственного сопротивле­ния Ro источника напряжения (рис. 1 .в) и собственной проводимости G₀ источники тока (рис.1 г). Уравнения рассматриваемых цепей получаются из 2-го закона Кирхгофа для рис.1 а, в и соответ­ственно 1-го закона Кирхгофа для рис. 1 б, г, сравнивая которые обнаруживаем их дуальность.

Для источника постоянного напряжения и источника постоян­ного тока уравнения имеют вид

U = E - R₀ I , (3)

I = J - G₀ U. (4)

Нетрудно видеть, что эти уравнения переходят друг в друга при G₀ = 1/R₀ , J = E/ R₀ . Уравнения (3) и (4) можно перепи­сать так U + R₀I = E и I +G₀ U = J.

В общем случае, для электрических цепей, содержащих контуры, с источниками напряжений и узлы, с которыми соединены источники тока, последние соотношения можно записать в форме обобщенных законов Кирхгофа.

Первый закон Кирхгофа: для произвольного узла алгебраическая сумма токов ветвей, соединенных с данных узлом, не содержащих источников тока, равна алгебраической сумме токов источников тока, соединенных с данным узлом

∑I_к = ∑J_к , (5)

Второй закон Кирхгофа: для произвольного контура алгебраичес­кая сумма напряжений на пассивных элементах, входящих в него, равна алгебраической сумме э.д.с, действующий в этом контуре

∑U_к = ∑E_к , (6)

В уравнениях (5) и (6) в дополнение к правилам знаков, сформулированных ранее, токи источников считаются положительны­ми, если они направлены в узел, а э.д.с. считаются положитель­ными, если они совпадают с принятым направлением обхода контура. Для источников, зависящих от времени законы Кирхгофа примут вид

(7) (8)

Использование той или иной формы записи законов Кирхгофа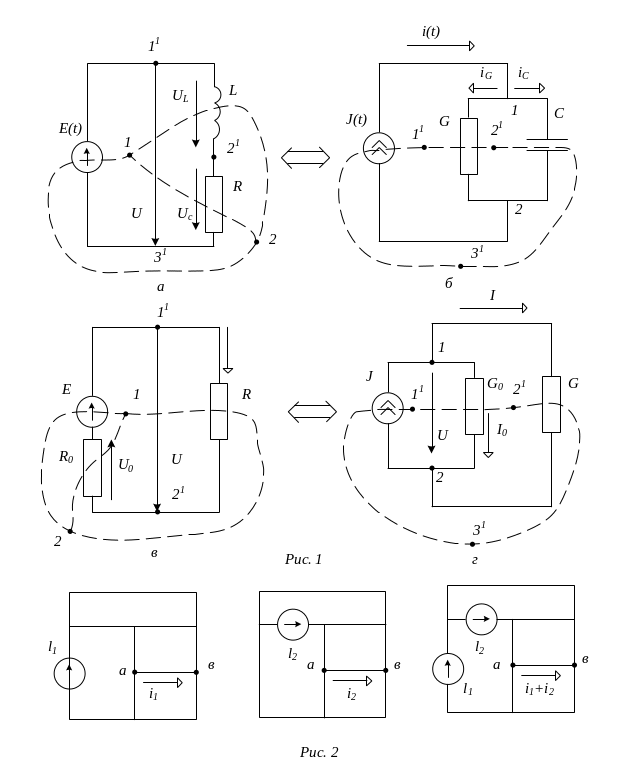 Определяется удобством в решении конкретной задачи. Переход от схемы цепи к дуальной схеме поясняется на рис.1.

Рассмотрим схему цепи на рис.1.а, в.Контур делит плоскость на две области: внутреннюю 1 и внешнюю 2. Если поместить там узлы 1 и 2 и соединить их между собой (пунктирной линией), пе­ресекая все элементы схемы, то заменив каждый элемент на дуаль­ный, можно получить дуальную цепь (рис. 1 б, г). Возможен так­же и обратный переход. Однако такие преобразования спра­ведливы только для планарных схем, т.е. схем, которые могут быть начерчены на плоскости без пересечения ветвей.

Нетрудно видеть, что дуальные схемы описываются дуальными уравнениями

- для схемы рис.1 в

- для схемы рис.1 б

Из этих примеров следует, что дуальными являются также такие геометрические (топологические) понятия кал контур и два узла, один из которых помещается во внутреннюю область плоскос­ти контура, а второй во внешнюю.

Таким образом, дуальны:

переменные (ток - напряжение);

параметры (сопротивление-проводимость);

топология (контур - два узла).

2. Элементарные сигналы

Генерирование, преобразование, передача и использование электрической энергии связаны со значениями, которые принимают ток и напряжение в рассматриваемых системах электроэнергетики. В системах электроники и автоматики ток и напряжение являются носителями информации (сигналами). Электрические цепи ЭВМ систем управления также представляют собой совокупности цепей, че­рез которые проходят сигналы. Входные сигналы представляют со­бой воздействие на систему, а выходные - ее отклики. В связи о этим анализ сигналов имеет важное значение.

Сигнал может быть описан аналитически , графически, таблицей. Для многих сигналов график временной зависимости дает все необходимые сведения о сигнале. Однако, имея в виду анализ процессов в электрических цепях, нахождение откли­ка (реакции) систем на заданные воздействия и определение свойств систем в ряде случаев удобней описывать сигнал путем раз­ложения его на элементарные аддитивные составляющие. Разложение сигнала на составляющие особенно важно для изучения линейных систем, выполняющих над сигналом линейные операции.

Возможность разложения сигнала возбуждения на элементарные составляющие и нахождение реакции по сумме отдельных откликов следует из принципа суперпозиции (наложения), согласно которому напряжение (ток), обусловленное одновременным действием несколь­ких источников, равно cyмме напряжений (тонов), обусловленных действием каждого из этих источников в отдельности.

Например, если в некоторой ветви (рис.2) ток при вклю­чении источника равен , а при включении то при действии обоих источников ток в этой ветви равен . С математической точки зрения линейной системой называется сис­тема, описываемая линейным уравнением, а с физической, -такая система, в которой выполняется принцип суперпозиции (разумеет­ся эти точки зрения не противоречивы). По принципу суперпо­зиции линейная система независимо обрабатывает каждую составляю­щую, как если бы других составляющих не существовало, и поэтому полный выходной сигнал системы находится простым сложением.

Выбор элементарных сигналов не является однозначным и поэ­тому наиболее часто используют лишь такие, которые отражают оп­ределенные физические процессы и могут быть с достаточной точ­ность» реализованы на практике. Например, для определения харак­теристик систем в автоматике используют следующие элементарные сигналы (возбуждения).

1. Функция единичного скачка или функция Хэвисайда (рис.3 а)

Умножая эту функцию на постоянные величины U или I, можно описать подключение цепи к источнику постоянного напряже­ния (рис.3 б, г) или источнику постоянного тока. Соответствующие входные ступенчатые сигналы записываются через элементарные в следующей форме:

Смешенные по оси времени на τ сигналы (рис.3 в) описыва­ются с помощью единичного скачка с "запаздывающим" аргументом

2. Импульсная функция или функция Дирака (рис.4 а)

Видно, что единичный импульс δ(t) определяется как бесконечно большой импульс бесконечно малой длительности, но ко­нечной площади равной единице. Пусть площадь реального электри­ческого импульса малой длительности равна U₀ , тогда реаль­ная импульсная функция напряжения определяется выражением

где размерности [ ] = [В с] = Вб, [ ]= C^-1 .

Для импульса тока площадью I₀

где размерность [I₀]= [A c ]= Кл .

Для индуктивной катушки U₀ приобретает физический смысл потокосцепления, а для конденсатора I₀ - заряда

Смещенная по оси времени δ - функция (рис.4 б) опреде­ляется отношениями

Сигнал произвольной формы можно представить используя совокуп­ность элементарных ступенчатых сигналов или импульсных Функций (рис. 3,4 в) .

Приведенные элементарные сигналы позволяют определить такие фундаментальные понятия линейных систем как переходную функцию (характеристики) и весовую функцию (импульсную реакцию) линейной системы. Знание последних позволяет определить отклик системы на произвольное воздействие в виде интегралов свертки (интегралов Дюамеля). Эти вопросы подробно рассматриваются в курсе теории автоматического управления.