Эйлерова характеристика. Фундаментальная группа

(Эйлерова характеристика некоторых подпространств пространства . Фундаментальная группа. Односвязность и стягиваемость)

Свойство топологического пространства называется топологическим, если оно сохраняется при гомеоморфизмах. Связность, существование разбивающих точек – топологические свойства. Познакомимся с еще одним таким свойством – эйлеровой характеристикой.

Рассмотрим поверхность параллелепипеда. Она имеет 6 граней, 12 ребер и 8 вершин. Число В–Р+Г=8–12+6=2. Если каждую грань параллелепипеда разбить диагональю на треугольники (в этом случае говорят о триангуляции поверхности), то число В–Р+Г будет равно 8–18+12=2, т. е. оно не изменится. Число 2 и есть эйлерова характеристика поверхности параллелепипеда.

Для вычисления эйлеровой характеристики поверхности рассматривают ее разбиение на вершины, ребра и грани. Элементы разбиения попарно не пересекаются. Они изображены на рисунке (вершина – это точка, ребро – это интервал, грань – это прямоугольник или треугольник без края):

– вершина; – ребро; – грань.

8

Эти элементы разбиения поверхности называются клетками. Вершина – это нульмерная клетка. Ребро – одномерная клетка – топологическое пространство, гомеоморфное интервалу (или прямой). Грань – двумерная клетка – топологическое пространство, гомеоморфное прямоугольнику без края (или плоскости).

Поверхность параллелепипеда гомеоморфна двумерной сфере . Простейшее клеточное разбиение сферы состоит из двух клеток: (любая) ее точка и дополнение к ней. Эйлерова характеристика сферы равна

.

Круг с краем называют диском. Его эйлерова характеристика равна 1.

Э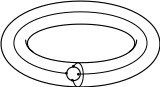 йлерова характеристика тора равна 0. Тор с одной дырой называется ручкой. Эйлерова характеристика ручки равна В–Р+Г = :

Э йлерова характеристика листа Мебиуса равна В–Р+Г = :

Для вычисления эйлеровой характеристики часто используют теорему о склейке по гомеоморфизму окружностей. Эта теорема утверждает, что при указанной склейке эйлеровы характеристики складываются. Приведем примеры использования этой теоремы. Рассмотрим – сферу, в которой вырезаны дыр. При заклеивании каждой ее дыры диском ее эйлерова характеристика увеличивается на 1. Так как в конечном итоге мы получаем , то .

Аналогично устанавливается, что эйлерова характеристика сферы с ручками и листами Мебиуса равна .

Познакомимся с еще одним топологическим свойством пространства – его фундаментальной группой.

Пусть и . Всякое непрерывное отображение , для которого , называется путем из в . Топологическое пространство называется линейно связным, если всякие две его точки можно соединить путем. Заметим, что всякое линейно связное пространство является связным, и что обратное неверно.

9

Предположим, что пространство линейно связно и отметим в нем некоторую точку . Всякое непрерывное отображение , для которого называется замкнутым путем или петлей в точке . Далее петлю в точке пространства будем называть просто петлей.

Назовем две петли и гомотопными, если одну из них можно непрерывно продеформировать в другую, находясь в пространстве . Формальное описание такой деформации таково: существует отображение произведения в пространство , удовлетворяющее условиям:

1) ;

2) .

Это отображение называется гомотопией от к . Гомотопность является отношением эквивалентности на множестве всех петель, и порождает разбиение этого множества на классы. Класс петли обозначается , а множество всех этих классов обозначается через .

На множестве определяется операция умножения.

Произведением классов петель и называется класс петли , определенной формулой

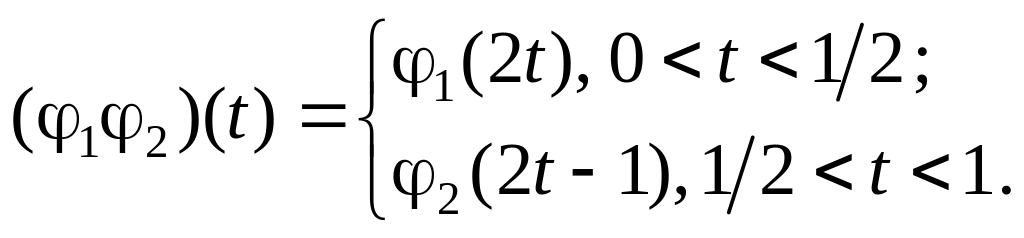
Относительно этой операции множество является группой, которая называется фундаментальной группой пространства в точке .

Мы предположили, что пространство линейно связно. Для такого пространства фундаментальные группы и изоморфны для любых точек . Поэтому часто фундаментальная группа линейно связного пространства обозначается просто через . Единицей этой группы является класс петли , являющейся постоянным отображением, Обратным элементом для класса является класс , где петля определяется так: .

Если линейно связные топологические пространства гомеоморфны, то их фундаментальные группы изоморфны.

Линейно связное топологическое пространство, имеющее тривиальную фундаментальную группу, называется односвязным.

Топологическое пространство, которое можно по себе продеформировать в точку, называется стягиваемым. Чтобы это понятие определить строго, нужно снова привлечь понятие гомотопии. Приведем ее определение. Непрерывные отображения (топологических

пространств) называются гомотопными, если существует такое непрерывное отображение , что . Отображение называется гомотопией от к .

Всякое стягиваемое пространство односвязно. Обратное утверждение неверно: сфера односвязна, но не стягиваема.

Примером пространства, имеющего нетривиальную фундаментальную группу, является окружность. Фундаментальная группа окружности изоморфна группе целых чисел.

10