2.2 Зертханалық жұмысқа тапсырма
2.2.1 VisSim бағдарламада (2.1) және (2.2) жүйелердің құрылымдық сұлбаларын жинаңыз.
2.23.2 (2.1) жүйе үшін әртүрлі k1 және k2 үшін өтпелі сипаттамалар мен фазалық траекторияларды тұрғызыңыз.
2.2.3 tпп=t(k1,k2, k1/k2) тәуелділікті зерттеңіз.
2.2.4 (2.2) жүйе үшін (2.10) ажыратып қосу заңын зерттеңіз.
3.2.5 с>λ, с=λ және с<λ режимдерді зерттеп, өтпелі сипаттамалар мен фазалық сүреттерін алыңыз. «Жылжымалы» режим үшін а1, а2, в параметрлері өзгергендегі процестерді зерттеңіз.
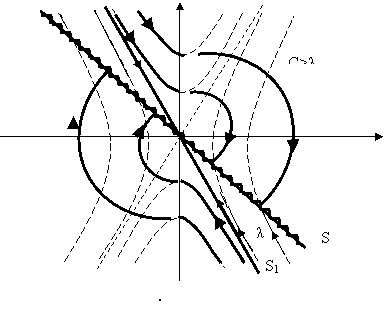
2.7 Сурет - Айнымалы құрылымы бар жүйе көмегімен тұрақты қозғалыстарды іске асыру
2.3 Зертханалық жұмыс бойынша есеп беру
Жұмыс бойынша есеп беру келесілерден тұрады:
- құрылым сұлбалары;
- таңдалынған коэффициенттердегі фазалық траекториялар;
- өтпелі сипаттамалар;
- өткізілген зерттеулер бойынша қорытындылар.
3 №3 Зертханалық жұмыс. Гармоникалық баланс әдісімен бейсызықты жүйеде автотербелістерді зерттеу
Жұмыс мақсаты; гармоникалық баланс әдісімен танысу және автотербелістердің параметрлерін анықтау
3.1 Жалпы мәліметтер
Бейсызықты жүйелер үшін кейбір шарттар орындалғанда автотербелістер режимі типтік болып саналады. Бұл режим іс жүзінде өте маңызды, мысалы екі позициялы реттеуіштер үшін. Сондықтан автотербелістер бар екендігін анықтағанымен олардың амплитудасы мен жиілігін анықтау қажет.
Автотербелістер параметрлерін тура анықтау үшін күйлер кеңістігі немесе периодты шарттарды қолдануға болады. Іс жүзінде жуықталған әдістер қолданылады – көбінесе бейсызықты жүйелерде пайда болатын тербелістердің гармоникалары сызықты буындар көмегімен басылады, яғни сызықты буындар төменгі жиіліктік фильтр болады.
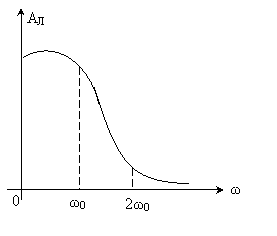
Егер де статикалық сызықты емес элемент кірісіне y=f(x) сипаттамасымен x(t)=Asinωt гармоникалық сигналды берсек, шығуда периодты тербелістер орнатылады; оларды Фурье қатарымен көрсетуге болады
Екіншісінен бастап, барлық гармоникаларда біріншіге қарағанда амплитудалары өте аз деп санап, оларды есепке алмаймыз.
Онда теңдеу келесі түрде жазылады
Симметриялық емес бейсызықтықтар үшін а0=0 болады, сонда
y(t)-ні x(t)-мен салыстырып, сызықты жиілік жүйелердің сипаттамалары сияқты сипаттамаларды енгізуге болады
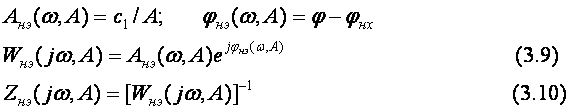
Бейсызықты жүйені келесі түрде көрсетуге болады (3.1 сурет).
Егер де сызықты емес элемент кірісіне ω1 жиілігі бар гармоникалық сигналды берсе, бекітілген жүйеде өшірілмейтін тербелістер пайда болады.
|
|
|
|
|
|
|
|
||
|
|
|
||
|
|
|
||
3.1 Сурет – Сызықты емес жүйе
Сондықтан, жүйе тұрақтылық шегінде орнатылған болады, ол келесі шартқа сәйкес
Егер де (2.13) және (2.14) теңдеулерінің нақты оң таңбалы (ωа, Аа) шешімі болса, онда жүйеде жиілігі ωа мен амплитудасы Аа автотербелістер пайда болуы мүмкін.
(2.13), (2.14) жүйесін графикалық шешуге болады. Ол үшін комплексті жазықтықта Wл(jω) сызықты бөліктің АФС-ын және бейсызықты Zнэ(А). элементтің инверсті АФС-ын құрады. Wл(jω) және Zнэ(А) годографтарының қиылысу нүктесі Аа амплитудамен ωа жиілікті анықтайды. Егер де годографтар
қиылыспаса, жүйеде автотербелістердің пайда болуы мүмкін емес. Және осы әдіс бойынша автотербелістер тұрақты болатынын шеше аламыз.
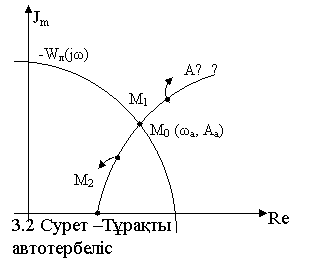
Мысалы, тербеліс амплитудалары өскенде Wл(jω) және Zнэ(А) қисықтар орналасуы Zнэ(А) қисық бойынша оң жаққа қозғалуды анықтайды (3.2 суретті қараңыз). Онда Wл(jω) және Zнэ(А) нүктесі автотербелістерге сәйкес. Егер әсер себебінен тербелістер амплитудасы өссе (Аа+ΔАа), онда бейсызықты элементтің жаңа күйіне М1 нүктесі сәйкестенеді, бұл нүкте АФС-ан тыс орнатылған. Сонымен бірге Wл(jω) < Zнэ(А), немесе Wраз (jω, А)<1, сондықтан бұл күйде жүйе тұрақтыға айнала бастайды, яғни тербелістер амплитудасы кеміп, бір уақыттан кейін бастапқы Аа шамаға тең болады.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
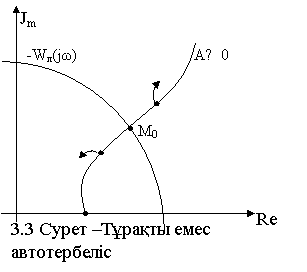
Егер де әсерлер себебінен автотербелістер амплитудасы Аа-ден кем болса, жүйенің жаңа күйіне М2 нүкте сәйкестенеді, бұл нүктеде жүйе тұрақсыз. Сонымен амплитуда өсе бастап, бастапқы Аа мәніне қайтады.
|
|
|
|
3. 4 Сурет – Тепе-теңдік күйдің тұрақтығы
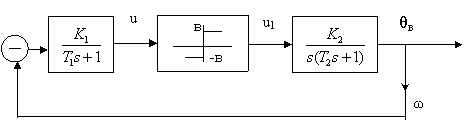
Мысал ретінде құрылымдық сұбасы 3.4 суретте келтірілген жүйенің тепе-теңдік күйінің тұрақтылығын зерттейік. Жүйе параметрлері В=1 В; k1 k2 =10 c-1; T1=10 c; T2=1 c.
Сызықты бөліктің теңдеуін жазамыз
(3.15)
Сызықты емес элемент үшін
u1(t)=q(A)u(t) (3.16)
мұндағы
(3.17)
(3.16) және (3.17) өрнектерін (3.15) теңдеуге қойып, аламыз
(3.18)
Бастапқы нөлдік шарттарда (3.18) теңдеуге Лаплас түрлендіруін қолданып , келесіні жазамыз
(3.19)
(3.19) теңдеуден сипаттама теңдеуін анықтаймыз
(3.20)
Теңдеудің периодты шешімінің болатынын Михайлов критерийімен тексереміз. Ол үшін (3.20) теңдеуге s=jω қойып, келесіні табамыз
(3.21)
Нақты және жорамал бөліктерін нөлге теңестіріп, келесіні аламыз
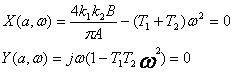(3.22)
Екінші теңдеуден периодты шешімнің жиілігін анықтаймыз
,
Біріншіден келесіні аламыз
(3.23)
Дайын q(а)= графигін қолданып (3.5 сурет), периодты шешімнің а амплитудасын табамыз.
|
|
|
|
Шешімнің тұрақтылығын анықтау үшін (3.22) өрнектердің туындыларын табу керек
Критерий қанағаттандырылады. Сондықтан, автотербелістер болады. q(а)=<k есепке алып (3.5 сурет), (3.23) теңдеуден автотербелістердің бар болатынының шарттары шығады
немесе
(3.24)
мұнда К = k1k2k— жалпы күшейту коэффициенті. Гурвиц критерийы бойынша (3.24) жүйенің тұрақты болмауының шарты болып табылады. Тұрақты болу шегі
сонымен бірге автотербелістер шегі болып табылады.
3.2 Зертханалық жұмысты орындауға тапсырма
3.2.1 Автоматты басқару жүйесінің шығуындағы автотербелістердің амплитудасы мен жиілігінің жүйе сызықты бөлігінің күшейту коэффициентінен тәуелдігін есептеп, графиктерін құру.
3.2.2. Гармоникалық сызықтандыру шарттарының орындалатынын тексеру.
3.2.3 Vissim немесе MathLab жүйелерінде 3.4 суретте келтірілген математикалық моделін құрастыру.
Сызықты емес элементтердің сипаттамаларын мұғалім береді, буындар параметрлері 3.1 кестеде орнатылған.
3.2.4 Тәжірибелерді жасап, сызықты емес элементтің статикалық сипаттамасы мен шығудағы сипаттамаларды алу.
З.1 К е с т е – Түйіндер параметрлері
№ в. |
Т1 |
Т2 |
ТЗ |
ВидНЭ |
В |
в |
tg а |
1 |
1 |
0.1 |
0.1 |
2а сурет |
50 |
- |
- |
2 |
1 |
1 |
0.1 |
2а сурет |
70 |
- |
- |
3 |
0.2 |
0.1 |
0.1 |
2а сурет |
60 |
- |
- |
4 |
1 |
0.1 |
0.1 |
26 сурет |
50 |
10 |
- |
5 |
1 |
1 |
0.1 |
2в сурет |
80 |
8 |
- |
6 |
1 |
0.5 |
0.1 |
2в сурет |
50 |
5 |
- |
7 |
1 |
0.5 |
0.1 |
2г сурет |
- |
10 |
1 |