Коммерциялық емес акционерлік қоғамы

Алматы энергетика және байланыс институты

Инженерлік кибернетика кафедрасы

 

 

 

 

Бейсызықты автоматты басқару жүйелердің теориясы

5В0702 - “Автоматтандыру және басқару” мамандығы үшін

зертханалық жұмыстарды орындауға арналған әдістемелік нұсқаулар

 

 

Алматы 2010

ҚҰРАСТЫРУШЫЛАР: Хисаров Б.Д., Аталыкова А.К., Бойко В.М. Бейсызықты автоматты басқару жүйелердің теориясы. 5В0702 - “Автоматтандыру және басқару” мамандығы үшін зертханалық жұмыстарды орындауға арналған әдістемелік нұсқаулар.– Алматы: АЭжБИ, 2010. –  19 б. 

Екінші ретті сызықты жүйелердің фазалық суреттерін зерттеу, айнымалы құрылымы бар жүйелерді зерттеу, бейсызықты автоматты басқару жүйелеріндегі автотербелістерді зерттеу сұрақтары қарастырылады.

 

 

1 №1 Зертханалық жұмыс. Екінші реттік жүйелердің фазалық траекторияларын зерттеу

 

Жұмыс мақсаты: бейсызықты жүйелердің фазалық жазықтықтағы  зерттеу әдісімен танысу; екінші реттік жүйелердің түбірлер және өтпелі сипаттамалар мен фазалық траекториялар арасындағы байланыстарды зерттеу.

 

1.1 Жалпы мәліметтер

  Бейсызықты жүйелерді де сызықты жүйлер сияқты зерттеу үшін фазалық траекториялар әдісін қолдануға болады.  Мысалға сызықты жүйені сипаттайтын екінші реттік дифференциалды теңдеуді қарастырайық

                                             ( 1.1)

мұндағы х – шығыстағы реттелетін шаманың тепе-теңдік күйінен ауытқуы.

Фазалық координаталарын еңгізейік  және (1.1) теңдеуін келесі түрде жазайық    

                                                                             (1.2)                           

яғни (х₁, х₂) жазықтықта жүйенің тепе-теңдік күйіне координат басы жатады.

(1.2) теңдеулерді интегралдайтын болсақ, фазалық траекториялардың теңдеулерін анықтаймыз

                                                       (1.3)

Функцияның түрі  коэффициенттеріне байланысты. Сонымен бірге бұл коэффициенттер осы жүйенің сипаттаушы теңдеудің түбірлерін анықтайды

                                     (1.4)

сондықтан,  түбірлер және 2-реттік жүйенің фазалық траектория арасында бір қалыпты тәуелділік.

Сонымен қатар оның келесідегідей алты жағдайы бар:

1)     түбірлер нақты және теріс таңбалы

            

 - жүйе орнықты;

2)     түбірлер комплексті және нақты теріс бөлшегі бар

             

- жүйе орнықты;

3)     түбірлер тек қана жорамал

           

- жүйе орнықтылық шекарасында;

4)     түбірлер комплексті және оң таңбалы нақты бөлшегі бар

             

- жүйе орнықсыз;

5)     түбірлер оң таңбалы нақты

            

- жүйе орнықсыз;

6)     түбірлер нақты және әртүрлі таңбалы

             

- жүйе орнықсыз.

Осы жағдайларды қарастырайық:

1) жүйеде апериодты түрде өшетін өтпелі сипаттама болады және (1.1) теңдеудің шешімі мынадай

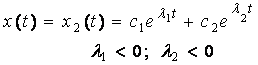                                             (1.5)

Уақыт бойынша екінші фазалық координата келесідегідей болады

                              (1.6)

Фазалық жазықтықта барлық траекториялар координат басына тоғысады және келесі екі асимптота бар болады:

      және  ;                                   (1.7)

2) өшетін тербелмелі процесс бар:

                                                    (1.8)

                                                      (1.9)

                                            (1.10)

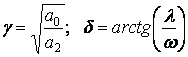                                                          (1.11)

(1.8), (1.10) теңдеулер фазалық жазықтықта спиралдар үйірін береді;

3) келесі шешім бар болады

                                                           (1.12)

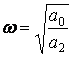,  яғни өшпейтін тербелістер болады.

Екінші фазалық координата мынадай

                                                     (1.13)

Фазалық траектория үшін теңдеу келесідегідей болады

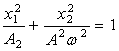                                                                       (1.14)

яғни фазалық траекториялар эллипстер болады;

4) теңдеудің шешімі келесідегідей:

                                            (1.15)

          

яғни шексіз өсетін амплитудалары бар тербелістер болады. Фазалық траектория – жайылмалы спираль;

5) теңдеудің шешімі келесідегідей:

                                                   (1.16)

                                     (1.17)

яғни шығу шама шексіз өседі. Фазалық жазықтықта екі асимптота пайда болады:

және                                           (1.18)

6) өтпелі сипаттама апериодтық болады, бірақ фазалық траектория алдынғысынан ерекше. Мысалы а₁=0. Онда (1.2) теңдеу мынадай түрде жазылады:

                                                  (1.19)

яғни             

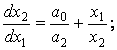                                                                     (1.20)

(1.20)-ны интегралдайтын болсақ, фазалық траектория гиперболар түрінде болады:                  

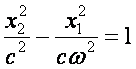                                                                 (1.21)

    Гиперболардың асимптоталары  түзу: , мұндағы ;

бір асимптота – тоғысатын, екінші - тоғыспайтын.