
- •Средние величины Формулы различных видов степенных средних
- •Структурные средние
- •·100% - Относительное линейное отклонение.
- •·100% - Коэффициент вариации.
- •Средние показатели динамики
- •Статистика численности работников и использования рабочего времени
- •Для анализа использования рабочего периода
- •Индексный метод анализа использования оф
- •Статистика основных и оборотных фондов
- •Степень использования оборудования
- •Статистика себестоимости
- •Статистика продукции
- •2. Анализ данных о выпуске продукции
Средние величины Формулы различных видов степенных средних
Значе-ние k |
Наименование средней |
Формула средней |
|
простая |
взвешенная |
||
−1 |
Гармоническая |
|
|
0 |
Геометрическая |
|
|
1 |
Арифметическая |
|
|
2 |
Квадратическая |
|
|
Структурные средние
Мода – значение признака, который наиболее часто встречается в совокупности (статистическом ряду).
В случае интервального ряда с равными интервалами, модальным интервалом считается интервал с наибольшей частотой, при неравных интервалах – с наибольшей плотностью.
Для
равных интервалов:
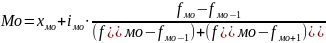 ,
где
,
где
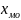 - нижняя граница модального интервала,
- нижняя граница модального интервала,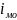 -
величина модального интервала,
-
величина модального интервала,
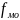 - частота модального интервала,
- частота модального интервала,
 - частота предмодального интервала,
- частота предмодального интервала,
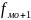 - частота постмодального интервала.
- частота постмодального интервала.
Медиана – значение признака, который лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.
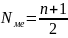 ,
где
,
где
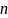 – число членов ряда.
– число членов ряда.
При
исчислении медианы интервального ряда:
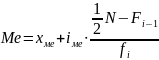 ,
где
,
где
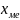 -
нижняя граница медианного интервала,
-
нижняя граница медианного интервала,
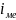 -
величина интервала разбиения,
-
величина интервала разбиения,
 -
накопленная частота интервала,
предшествующего медианному,
-
накопленная частота интервала,
предшествующего медианному,
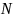 - число наблюдений,
- число наблюдений,
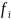 -
частота медианного интервала.
-
частота медианного интервала.
ПОКАЗАТЕЛИ ВАРИАЦИИ
Абсолютные показатели вариации
1. Размах вариации (R): = Xmax−Xm𝑖n
2.
Среднее линейное отклонение. а)
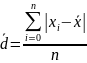 - для несгруп. данных. б) для вариац-го
ряда
- для несгруп. данных. б) для вариац-го
ряда
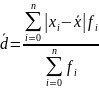 .
.
3.
Дисперсия
 - для несгруппированных данных.
- для несгруппированных данных.
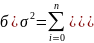 - для вариационного ряда
- для вариационного ряда
4.
Среднее квадратическое отклонение:
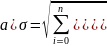 ;
;
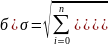
Относительные величины вариации.
вычисляются как отношение абсолютных показателей вариации к средней арифметической (или к медиане), выражаются в %.
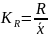 ·100%
- коэффициент
осцилляции.
·100%
- коэффициент
осцилляции.·100% - Относительное линейное отклонение.
·100% - Коэффициент вариации.
 +
Кравномерности
=
100%; Кравномерности
=
100 –
+
Кравномерности
=
100%; Кравномерности
=
100 –

ПОКАЗАТЕЛИ ДИНАМИКИ
|
Показатели |
Метод расчета |
|
С переменной базой (цепные) |
С постоянной базой (базисные) |
||
1. |
Абсолютный прирост,( Δ) |
∆ =
|
|
2. |
Коэффициент роста (Кр) |
Кр
=
|
|
3. |
Темп роста (Тр),% |
Тр = Кр∙100 |
|
4. |
Темп прироста (Тп),% |
Тп = (Кр−1)∙100 Тп
=
Тр
−100 ; Тп
=
|
=
−100 ;
= |
5. |
Абсолютное значение 1% прироста (А) |
А= |
|
Средние показатели динамики
Показатель |
Метод расчета |
а) для интервального ряда
б) для моментного ряда с равными интервалами
в) для моментного ряда с неравными интервалами |
|
|
|
|
|
|
= |
|
|
|
|

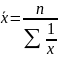
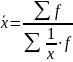
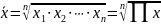

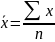
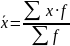
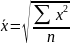
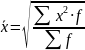
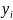 −
−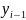
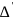 =
−
=
−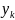
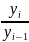
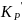 =
=
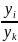
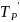 =
∙100
=
∙100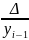 ∙100
∙100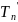 =
=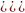 −1)·100
−1)·100
 ,
А =
,
А =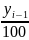
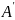 =
=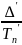 ,
=
,
=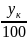
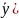
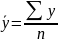
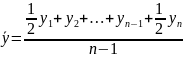
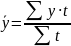
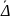 )
) или
или
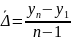
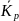 )
)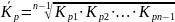 или
или
 ,
,
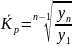
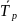 ),
%
),
%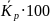
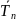 ),
%
),
%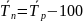 или
или
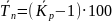
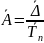 .
.