3. Метод интегрирования по частям.
Основная идея
метода – по формуле
перейти от сложного интеграла к более
простому.
Этим методом,
например, решают интегралы вида
,
где
– многочлен (в частности, степенная
функция
),
а
– одна из следующих функций:
,
,
,
,
,
.
Пример 6.
Вычислить
.
Заметим, что под
интегралом содержится произведение
многочлена
и функции
.
Обозначим
и
,
то есть исходный пример представим в
виде
.
Его можно свести к более простому по
формуле интегрирования по частям. Для
того чтобы ей воспользоваться, нужно
вычислить
и
(константу С не пишем, ее добавим в
конце примера). Подставим найденные
выражения в формулу, получим следующее
решение:
.
4. Интегрирование рациональных дробей (частный случай различных действительных корней знаменателя).
Определение 3.
Рациональной дробью называется функция
вида
,
где
и
– многочлены
-ой
и
-ой
степени.
Определение 4.
Дробь называется правильной, если
,
в противном случае дробь называется
неправильной.
Утверждение 1.
Всякую неправильную дробь
можно представить в виде суммы
,
где
– многочлен («целая часть»), а
– правильная дробь. Для выделения целой
части применяется прием «деление
столбиком».
Утверждение 2.
Если знаменатель правильной рациональной
дроби
имеет
различных действительных корней
,
то эта дробь представима в виде суммы
простейших дробей
,
где числа
находятся методом неопределенных
коэффициентов.
План интегрирования рациональных дробей.
1. Если дробь неправильная, представить ее в виде суммы многочлена и правильной дроби.
2. Правильную дробь представить в виде суммы простейших.
3. Проинтегрировать многочлен и простейшие дроби.
Пример 7.
Вычислить
.
Действуя по приведенному выше плану, получаем следующее решение:
1. Так как дробь, стоящая под знаком интеграла, неправильная, выделим целую часть «делением столбиком»:
Итак, получили, что исходная неправильная рациональная дробь представима в виде суммы многочлена и правильной дроби:
.
Многочлены интегрируются по первому табличному интегралу, следовательно, осталось научиться интегрировать правильные рациональные дроби.
2. Представим
полученную правильную дробь в виде
суммы простейших. Корни знаменателя
равны
и
.
Значит, эта дробь разлагается на сумму:
(приведем
ее к общему знаменателю)
и сравним дроби слева и справа. Они
равны, их знаменатели равны, значит, и
числители должны быть тоже равны.
Следовательно, должны быть равны
коэффициенты при одинаковых степенях
.
Приравняем их:
Решением этой
системы являются числа
Итак, правильная дробь представима в виде
.
3. Проинтегрируем:
.
§2. Определенный интеграл
Определение 5.
Пусть функция
задана на отрезке
.
Разобьем отрезок
на
произвольных частей точками
.
Обозначим длины отрезков
.
Выберем на каждом из отрезков
произвольную точку
.
Сумма вида
называется
частичной суммой. Определенным интегралом
от функции
на отрезке
называется предел этой частичной суммы
,
если он существует и не зависит от выбора
точек
и
.
Обозначение 2.
.
Формула Ньютона-Лейбница (связь определенного и неопределенного интегралов)
,
где
– первообразная функции
.
Пример 8.
Вычислить
.
.
Формула замены переменной в определенном интеграле.
.
Пример 9.
Вычислить
.
.
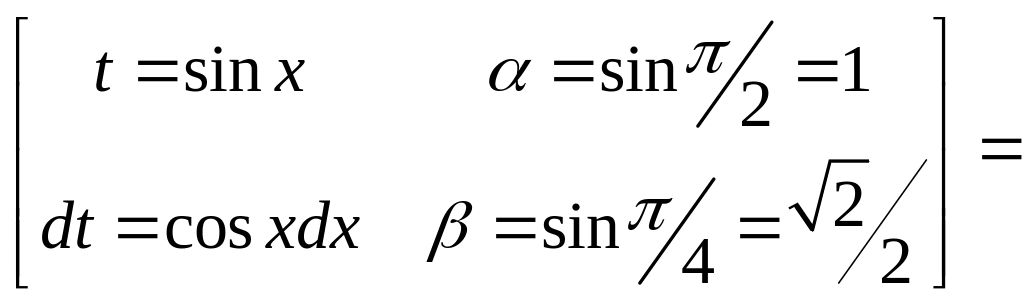
Формула интегрирования по частям в определенном интеграле
.
Пример 10.
Вычислить
.
.
§3. Приложения определенного интеграла
1. Вычисление
площадей плоских фигур.
Пусть фигура ограничена
линиями
и
,
причем на отрезке
выполняется неравенство
,
т.е. график функции
лежит не ниже графика функции
.
Тогда площадь этой фигуры находится по
формуле
,
где
и
(абсциссы точек пересечения этих линий)
находятся из уравнения
.
Пример 11. Найти
площадь фигуры, ограниченной линиями
и
.
Уравнение
задает параболу, уравнение
задает прямую. Найдем их точки пересечения,
решив для этого уравнение
и
.
Начертим графики этих линий. Требуется найти площадь заштрихованной фигуры:
Так как на отрезке
парабола расположена выше прямой, то
площадь заштрихованной фигуры находится
с помощью следующего интеграла:
кв.ед.
2. Вычисление
объемов тел вращения.
Пусть функция
непрерывна и неотрицательна на отрезке
.
Тогда тело, образованное вращением
графика этой функции вокруг оси
,
имеет объем
Пример 12. Найти
объем тела, полученного вращением кривой
на отрезке
вокруг оси
.
Для нахождения объема вычислим интеграл
42
куб.ед.