Лабораторная работа №7 Обработка результатов прямых равноточных измерений

Цель работы: провести обработку результатов прямых многократных равноточных измерений для представления в интервальном виде.

Оборудование, оснастка, инструмент:

1. Измерительная стойка по ГОСТ 10197-70.

2. Оптикаторная головка по ГОСТ 28798-90.

3. Набор плоскопараллельных концевых мер длины по ГОСТ 9038-90.

4. Микрометр по ГОСТ 6507-90.

Основные теоретические положения

Измеренное значение при однократном измерении можно определить выражением вида:

Q_i = q_i[Q] + _i, (7.1)

где q_i[Q] - результат измерения (однократного);

_i –суммарная поправка.

Значение измеряемой величины при многократном измерении:

(7.2)

Такое представление результатов является неполным, т.к. в нем нет информации о характере неопределенности результата измерения. Под неопределенностью понимают параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые можно приписать измеряемой величине.

Действительно, т.к. в результаты реальных измерений зависят от большого числа разнообразных факторов, зависимость результата каждого отдельного измерения можно представить в виде:

Q_i = F(x₁, x_2, …..x_n), (7.3)

где x_i – переменные функциональные параметры.

Наличие случайной погрешности формирует рассеяние результатов многократных измерений относительно некоторого центра – математического ожидания. Результат каждого отдельного измерения - отсчёт - является случайным числом. При измерениях идентичной характеристики одной детали, полученных одним измерительным оборудованием, используемым несколько раз одним оператором рассеяние результатов измерений характеризуется сходимостью (изменчивостью). Такие погрешности описываются с помощью законов математической статистики.

Систематические погрешности, в свою очередь, вызывают смещение результата измерения на некоторое конечное, как правило, фиксированное значение. Однако, систематические погрешности могут проявляться в виде переменного отклонения результата измерения от истинного значения физической величины (прогрессирующие, циклически изменяющиеся и др).

Каждый параметр x_i может иметь отклонение x_i (погрешность) от предписанного значения. Поскольку погрешность x_i мала по сравнению с величиной x_i, суммарная погрешность Q_i функции Q_i можно вычислять по формуле:

, (7.4)

где y/x_i – передаточное отношение параметра x_i.

Данная формула справедлива для систематических погрешностей x_i. Для случайных погрешностей (когда отдельные составляющие не всегда принимают предельные значения) используется теорема теории вероятностей о дисперсии, то есть:

(7.5)

Суммарная погрешность при наличии только случайных составляющих x_i погрешностей:

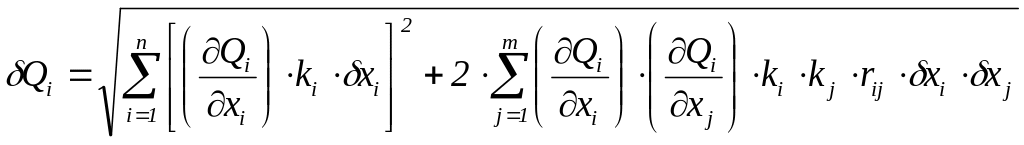, (7.6)

где m – число попарно корреляционно связанных параметров;

k_i и k_j – коэффициенты относительного рассеяния, характеризующие степень отличия закона распределения погрешности данного параметра от нормального;

r_ij – коэффициент корреляции, существующий при наличии корреляционной связи между параметрами x_i и x_j.

Значения обоих видов погрешностей целесообразно привести в виде предельной погрешности измерения, определяемой числовыми значениями погрешностей измерения от всех составляющих:

, (7.7)

где знаки «+» или «-» ставятся из условия, чтобы систематические и случайные погрешности суммировались по модулю.

Если в случайной погрешности известно среднее квадратическое отклонение, то:

, (7.8)

где k – показатель, указывающий доверительные границы для предельной случайной погрешности измерения и определяемый выбранным значением доверительной вероятности P и видом закона распределения. Чаще всего предполагают, что измеренные значения физической величины распределены нормально, но в случае ограниченного набора значений измеренной величины пользуются характеристиками распределения Стьюдента.

Методика получения результатов при проведении многократных измерений установлена ГОСТ 8.207-76 и представляет собой последовательное выполнение следующих этапов:

1. Определение наличия грубых погрешностей и исключение промахов.

При обработке уже имеющихся результатов наблюдений произвольно отбрасывать отдельные результаты нельзя, так как это может привести к фиктивному повышению точности результата измерения. Поэтому применяют следующую процедуру. Вычисляют среднее арифметическое результатов наблюдений х_i по формуле:

. (7.9)

Затем вычисляют оценку СКО результата наблюдения как:

. (7.10)

Находят отклонение v_п предполагаемого промаха x_п от :

v_п =  x_п - . (7.11)

По числу всех наблюдений n (включая x_п) и принятому для измерения значению Р находят z(P,n) – нормированое выборочное отклонение нормального распределения. Если v_п < zS(x), то наблюдение x_п не является промахом; если v_п  zS(x), то x_п – промах, подлежащий исключению. После исключения x_п повторяют процедуру определения и S(x) для оставшегося ряда результатов наблюдений и проверки на промах наибольшего из оставшегося ряда отклонений от нового значениям (вычисленного исходя из n – 1).

2. Исключение известных систематических погрешностей из результатов наблюдений.

3. Вычисление точечных оценок исправленных результатов измерений. Случайную составляющую, характеризуемую СКО результата измерения, оценивают по формуле (7.10).

4. Проверку гипотезы о нормальности закона распределения результатов измерений. Проверку выполняют с помощью критериев, изложенных в ГОСТ 8.207-76 или ГОСТ Р ИСО 5479-2002. при выполнении работы рекомендуется использовать методику проверки нормальности распределения по составному критерию, приведенную в Приложении А.

5. Вычисление доверительных границ случайной погрешности.

Доверительные границы случайной погрешности результата измерения при доверительной вероятности Р находят по формуле:

(P) = t(P,n)  S(x) , (7.12)

где t – критерий Стьюдента.

6. Вычисление доверительных границ систематической погрешности.

Доверительные границы НСП результата измерения (P) вычисляют по формуле:

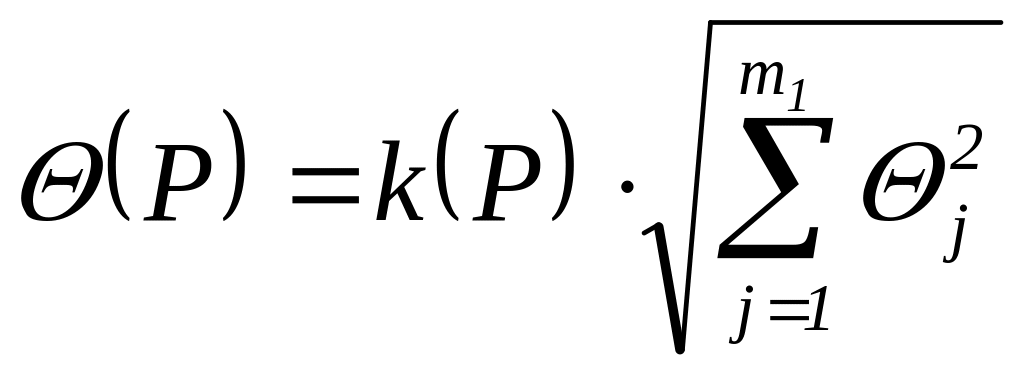, (7.13)

где k(P) – коэффициент, определяемый принятой Р и числом m₁ составляющих НСП;

(P) – найденные нестатистическими методами границы j-ой составляющей НСП (границы интервала, внутри которого находится эта составляющая, определяемые при отсутствии сведений о вероятности ее нахождения в этом интервале; при Р = 0,95 принимают k(P) = 1,1).

Если составляющие НСП распределены равномерно и заданы доверительными границами (P), то доверительную границу НСП результата измерения вычисляют по формуле:

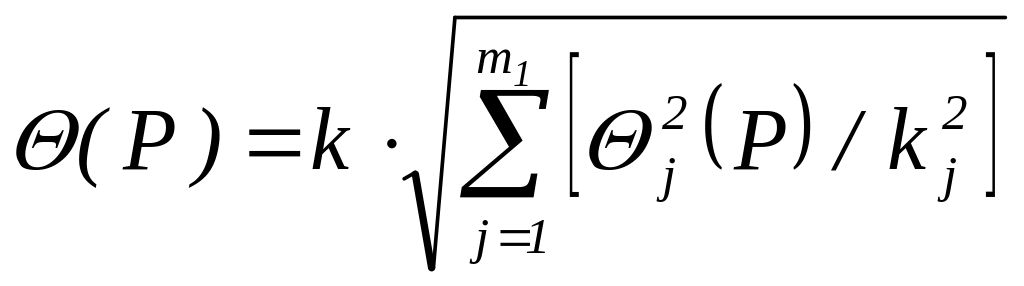, (7.14)

где k и k_j - те же, что и в предыдущем случае, коэффициенты, соответствующие доверительной вероятности Р и Р_j соответственно; m₁ - число составляющих НСП.

7. Вычисление доверительных границ погрешности результата измерения.

Для суммирования систематической и случайной составляющих погрешностей рекомендуется следующий способ:

Если (P)/S(x) < 0,8, то НСП (P) пренебрегают и окончательно принимают (P) за погрешность результата измерения (P) при доверительной вероятности Р.

Если (P)/S(x)  8, то пренебрегают случайной погрешностью и принимают (P) = (P).

Если 0,8  (P)/S(x)  8, то доверительную границу погрешности результата измерений вычисляют по формуле:

, (7.15)

где K_() = ;

.

8. Формирование результата измерения.

При окончательном представлении результат измерения следует привести в виде доверительных границ:

, (7.16)

где – среднее результатов многократных измерений, освобожденное от значений грубых ошибок (промахов).

Оборудование

Оптикатор – это измерительная пружинно-оптическая головка (рисунок 7.1), прибор для высокоточных измерений линейных размеров и отклонений от заданных геометрических форм, в котором пружинный преобразовательный механизм микрокатора используется в сочетании с оптической системой.

Головка предназначена для линейных измерений и может применяться в различных измерительных устройствах и приспособлениях.

Рисунок 7.1 – Головка измерительная пружинная

Оптикатор имеет следующие метрологические характеристики:

• цена деления 0,2мкм;

• диапазон измерений ± 25 мкм;

• измерительное усилие 1,5 Н;

Погрешность измерения всех указанных оптиметров составляет 0,5 деления шкалы. Основные характеристики определяются ГОСТ 28798-90.

Перед проведением измерений на оптикаторе необходимо выполнить следующие подготовительные операции:

• освободить застопоренный фиксатором измерительный стержень 5;

• включить в сеть трансформатор и подключить осветитель 1 головки к трансформатору, установив предохранитель предварительно в положение, соответствующее напряжению в сети;

• прогреть головку в течение 20-30 мин;

• отрегулировать яркость светового индекса ручкой на трансформаторе;

• установить головку на точный размер с помощью винта 3;

• установить указатели поля допуска с помощью маховичков 2;

• установить арретир 4;

• установить световой индекс на шкале в поле зрения.

В оптикаторе вместо стрелочного указателя (в отличие от микрокатора) применен так называемый оптический рычаг, который состоит из осветителя 1 и зеркала 6, приклеенного к пружине 7 (рис. 7.2).

Луч света, пройдя через отверстие 3 с нитью посредине и отразившись от зеркала 6 в виде «зайчика», передает на шкалу 4 изображение нити, которое и является указателем. Оптикатор обладает всеми положительными качествами микрокатора, кроме того, имеет большие пределы измерения.

В механизме оптикатора вместо обычных шарниров качения и скольжения применены пружинные шарниры. Принцип действия шарнира основан на упругих свойствах закрученной вдоль своей оси плоской пружины. Поворот среднего сечения такой пружины относительно продольной оси пропорционален усилию, растягивающему эту пружину. Зеркало расположено на средней части спиральной пружины, один конец которой закреплен неподвижно, а другой прикреплен к плоской пружине, соединенной с измерительным стержнем. При перемещении стержня вдоль направляющей раскручивается спиральная пружина и поворачивает зеркало, которое перемещает изображение щели вдоль шкалы (светлый индекс).

Рисунок 7.2 – Оптическая схема оптикатора: 1 – лампа; 2 – конденсатор; 3 – щель; 4 – шкала; 5 – объектив; 6 – зеркало; 7 – спиральная пружина; 8 – диафрагма; 9 – измерительный стержень

Последовательность выполнения работы