Тема 2.4. Эквивалентные автоматы, преобразования автоматов.
Два
автомата
и
с одинаковыми входными и выходными
алфавитами называются эквивалентными,
если после установки их в начальные
состояния их реакции на любое входное
слово совпадают.
Для данного автомата Мили всегда можно построить эквивалентный ему автомат Мура, и наоборот.
Поскольку
эквивалентность автоматов определяется
через их реакцию, то при преобразованиях
автоматов модели Мили в модель Мура и
наоборот выходным сигналом автомата
Мура
,
связанным с начальным состоянием будем
пренебрегать.
П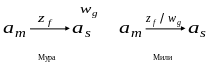
реобразование
автомата Мура в автомат Мили
Дан автомат Мура :
Построим автомат Мили :
При этом возьмем:
,
,
,
,
Осталось
определить функцию
.
Если
в автомате Мура
и
,
то в автомате Мили возьмем
.
Это
значит, что выходной сигнал
переносится на все дуги, входящие в
вершину
.
П
ример:
При табличном способе задания автоматов
таблица переходов совпадает с таблицей переходов ;
таблица выходов получается из таблицы переходов заменой символа
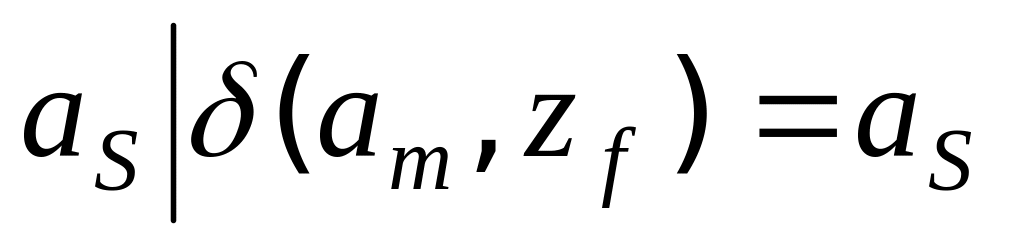символом
.
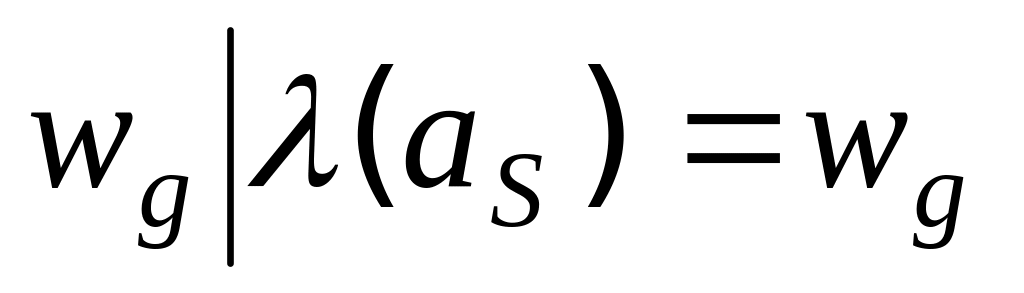Из самого способа построения автомата Мили очевидно, что он эквивалентен автомату Мура .
Преобразование автомата Мили в автомат Мура
Каждая
пара
,
где
- сигнал на стрелке входящей в
,
графа автомата Мили порождает отдельную
вершину
,
отмеченную сигналом
,
в графе автомата Мура.
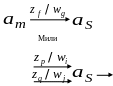
Дан автомат Мили :
Построим автомат Мура :
Необходимым условием эквивалентности автоматов является:
, .
1)
Определим
:
Каждому
состоянию
поставим в соответствие множество
всех пар вида
,
где
- выходной сигнал, приписанный дуге,
входящей в вершину
.
Пример:
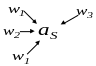
Число элементов в можно взять равным числу дуг, входящих в , но достаточно взять столько элементов, сколько различных сигналов приписано входящим дугам.
Множество состояний автомата получим объединением множеств .
,
где
- количество состояний в
.
2)
Определим
и
.
2.1. Каждому состоянию , представляющему собой пару вида поставим в соответствие выходной сигнал .
2.2.
Если в
был переход
и при этом
,
то в
будет переход из множества состояний
,
порождаемых состоянием
,
в состояние
под действием того же входного сигнала
.
3)
В качестве начального состояния
можно взять любое из состояний множества
,
порождаемого состоянием
.
Пример:
Дан
автомат Мили
.
В
автомате
имеем:
,
,
,
,
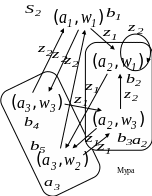и
определяются графом автомата.
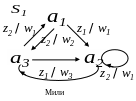
Рассмотренные
преобразования автоматов показывают,
что при преобразовании Мура
Мили
количество состояний автомата сохраняется.
При преобразовании Мили
Мура
количество состояний может увеличиваться.
Таким образом, эквивалентные автоматы могут иметь различное число состояний. В связи с этим возникает задача нахождения автомата эквивалентного данному с минимальным числом состояний.
Лекция 5.