Тема 4.3. Конечные автоматы как распознаватели.

Итак, существует иерархия формальных грамматик. Иерархии формальных грамматик соответствует иерархия формальных языков. С другой стороны, типы языков могут быть определены типами абстрактных распознающих устройств (автоматов). При этом язык определяется как множество цепочек, допускаемых распознающим устройством. Таким образом, между формальными языками, формальными грамматиками и абстрактными автоматами имеются взаимно однозначные соответствия, показанные на рис.3.1.

Распознаватели (акцепторы)

Выше рассматривались вопросы, связанные с заданием языков с помощью грамматик, т.е. с помощью механизма порождения цепочек языка.

Как отмечалось ранее, язык может задаваться с помощью распознавателей, т.е. с помощью механизма распознавания цепочек языка. В качестве таких распознавателей будут рассмотрены в первую очередь конечные автоматы (автоматы с конечным числом состояний) специального типа, называемые акцепторами.

Содержательное описание акцептора

На содержательном уровне распознаватель можно представить состоящим из трех частей:

• входной ленты;

• управляющего устройства с конечной памятью;

• вспомогательной или рабочей памяти.

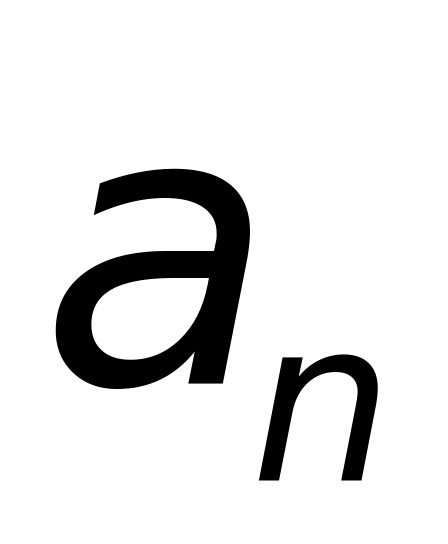
Входная лента

Р и с. 3.2

Входная лента – линейная последовательность клеток, или ячеек, каждая из которых содержит точно один символ из некоторого конечного алфавита. На ленте находится цепочка символов алфавита , ограниченная особыми концевыми маркерами не являющимися символами алфавита . Маркеры могут стоять с обеих сторон, либо только справа, либо маркеров может не быть.

Управляющее устройство с конечной памятью имеет входную головку, которая в каждый момент времени читает (или, как говорят, обозревает) одну ячейку ленты. Передвигаясь вдоль ленты в дискретные моменты времени головка символ за символом считывает цепочку символов с ленты. Обычно входная головка только читает.

Распознаватель, который никогда не передвигает входную головку влево, называется односторонним.

Рабочей памятью может быть хранилище информации любого типа. Хранящаяся в памяти информация построена из символов алфавита памяти.

Если распознаватель представляет собой конечный акцептор, то он решает задачу распознавания не прибегая к использованию рабочей памяти и работает при этом как односторонний.

Работа конечного акцептора представляет собой некоторую последовательность тактов. Содержание такта определяется состоянием управляющего устройства и входным символом, считываемым в данный момент входной головкой. Такт состоит из изменения состояния и сдвига входной головки на одну ячейку вправо.

Детерминированный акцептор

Детерминированный акцептор с конечным числом состояний (конечный акцептор, анализатор) задается пятеркой:

, где

- конечное множество состояний;

- конечное множество допустимых входных символов;

- отображение множества в множество :

. Для детерминированного акцептора это отображение является функциональным, и называется функцией переходов;

- начальное состояние акцептора;

- множество состояний, называемых заключительными или принимающими состояниями акцептора: .

Пара называется конфигурацией автомата , если (т.е. если ). В процессе работы акцептора цепочка представляет собой последовательность символов на входной ленте, начинающуюся с символа, обозреваемого головкой в состоянии , и всеми символами еще не считанными с ленты, т.е. находящимися справа от обозреваемого символа.

Конфигурация называется начальной. При этом - это цепочка символов, которая должна быть проанализирована акцептором и либо принята им (классифицирована как принадлежащая языку , задаваемому акцептором), либо отвергнута как не принадлежащая языку .

Пара , где называется заключительной или допускающей. означает, что вся входная цепочка считана с ленты.

Такт автомата представляется бинарным отношением ⊢ (или ⊢, если подразумевается), определенным на конфигурациях.

Отношение ⊢ означает следующее:

• автомат находится в состоянии и его входная головка обозревает ячейку ленты с символом ;

• в результате выполнения данного такта автомат перейдет в состояние и сдвинет входную головку на одну ячейку вправо.

Необходимо отметить, что существуют грамматические модели, не входящие в иерархию Хомского. Такие грамматики были разработаны в процессе поиска порождающих механизмов, которые бы лучше представляли весь синтаксис и/или семантику языков программирования.

Лекция 8.