§11.1. Сандық қатарлар
1. Сандық қатар және оның қосындысы.
─
сандық
қатардың n-дербес
қосындысы деп
аталады.
Егер
(11.2)
бар және ақырлы болса, онда сандық қатар жинақты, ал (11.2) шек жоқ немесе шектелмеген болса, қатар жинақсыз деп аталады. Берілген (11.1) қатардың шегі болатын S саны оның қосындысы деп аталады.
М.1*.
а)
; ә)
;
б)
;
қатарларын жинақтылыққа зерттеп, егер
жинақты болса олардың қосындысын
табайық.
Шешу.
а)
Берілген қатардың мүшелері
еселігі
болатын, геометриялық прогресия болып
табылады. Ендеше, оның алғашқы
-мүшесінің
қосындысы,
(*)
өрнегімен
анықталады. Бұдан
болғанда
,
ал
болатындығын көреміз. Еендеше, (*)
n-дербес
қосындыдан шекке көшсек,
болғанда қатардың қосындысы
болып шығады. Демек, қатар жинақты.
Егер
де,
болса, берілген қатар жинақсыз.
ә)
Берілген сандық қатардың бөлімін
түрлендіру арқылы, жәй бөлшектерге
жіктейік. Сондықтан,
болғандықтан
.
(1)
Онда (1) жәй бөлшекті пайдаланып берілген сандық қатардың n-дербес мүшесін мына түрде жазуға болады:
(2)
Енді бұл қосындыны жеке-жеке ашып жазайық,
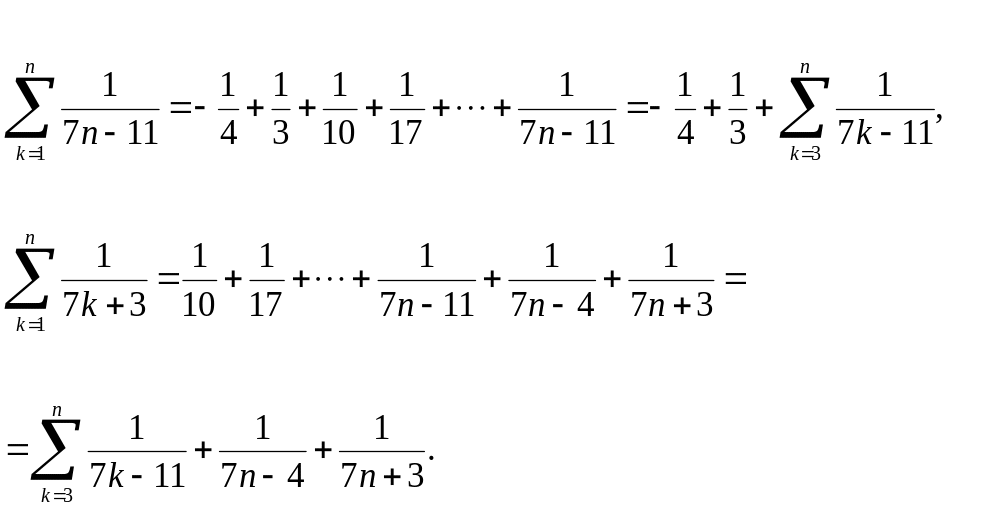
Онда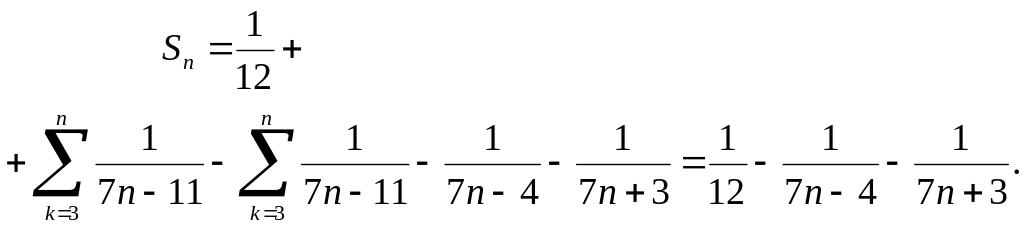
Демек, (11.2) шекті тапсақ
Ендеше,
берілген сандық қатар жинақты, ал оның
қосындысы
.
б) Жаңағы тәсіл бойынша қатар астындағы өрнекті жәй бөлшектерге жіктейік
Онда
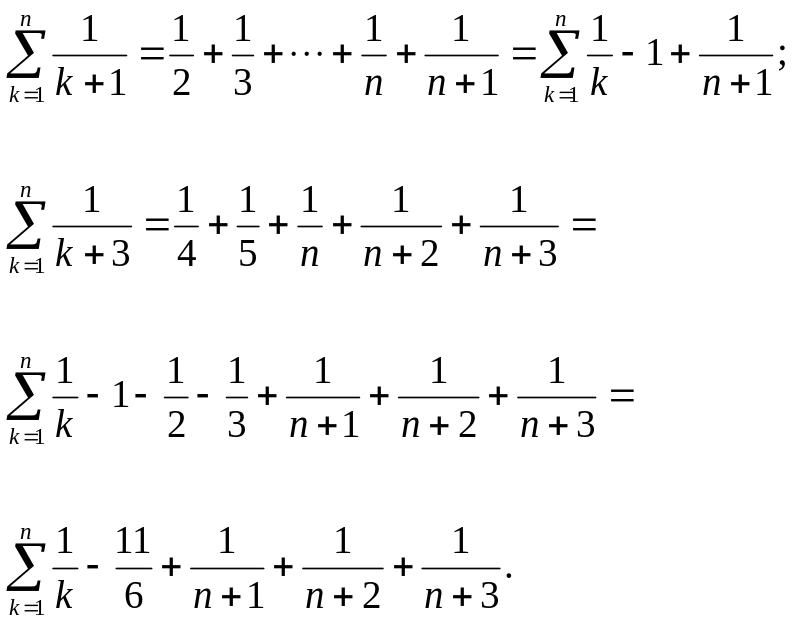
Енді берілген қатарға сәйкес n-дербес қосындыны құрайық, яғни
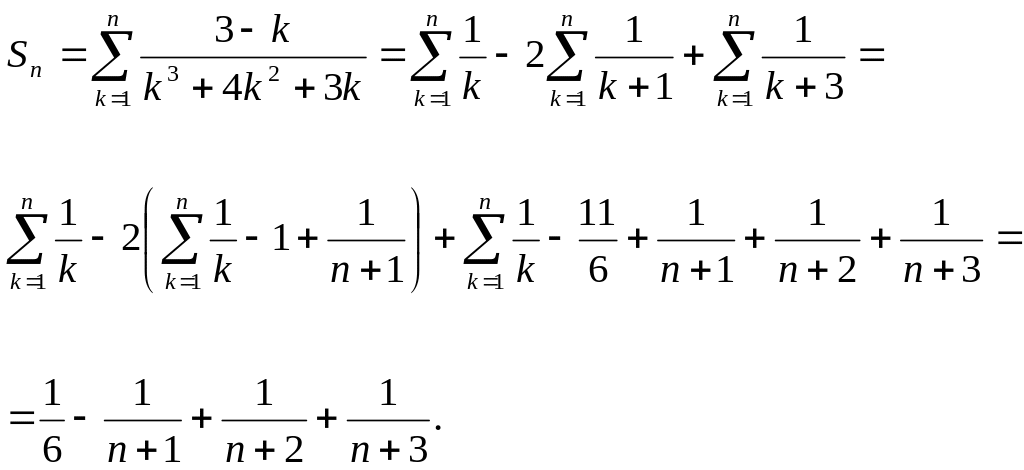
Ендеше,
Бұдан
берілген қатар жинақты, ал оның қосындысы
болсын.
(11.3)
қалдық қатар деп аталады.
М. 4*.
а)
,
ә)
қатарларын жинақтылыққа зерттейік.
Шешуі. а) Бірінші қатардан
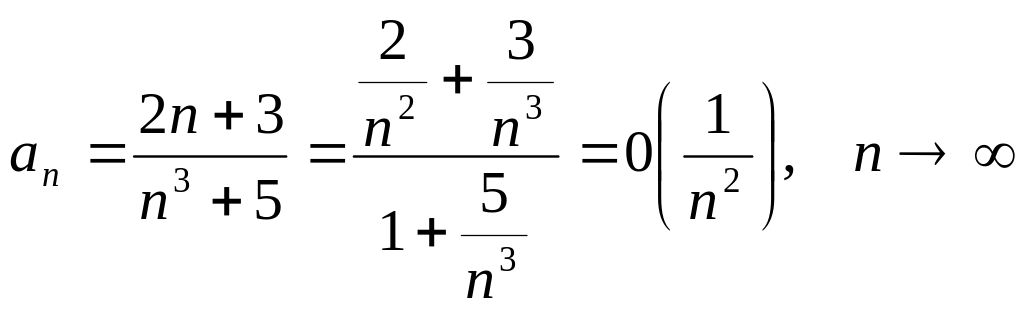
Болғандықтан,
оны
бигармоникалық жинақты қатармен (М, 3*)
салыстырайық. Онда (11.7) қатынасты
қарастыралық
.
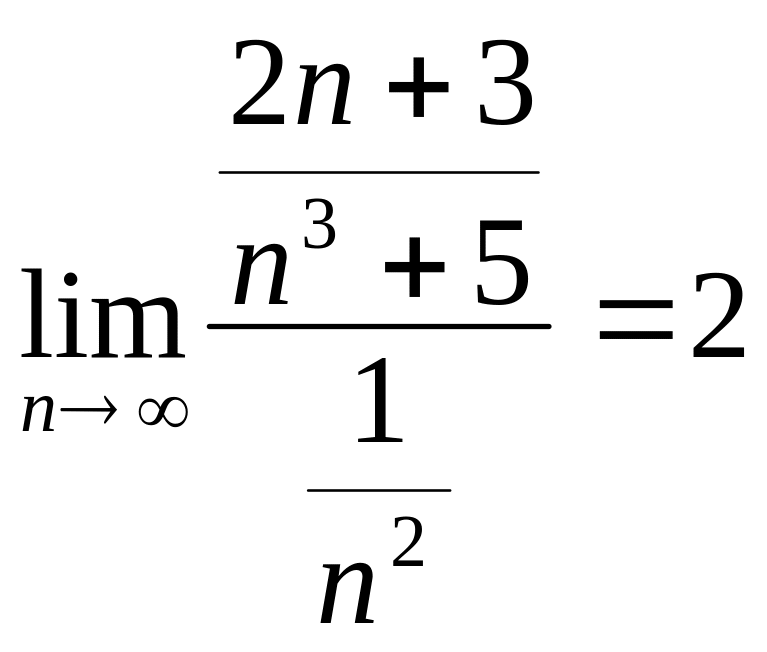Ендеше, 11.5 теорема бойынша берілген а) қатары жинақты.
ә)
Бұл қатарды
гармоникалық жинақсыз қатармен (М. 3*)
салыстырайық, 11.5-шектік теорема бойынша,
.
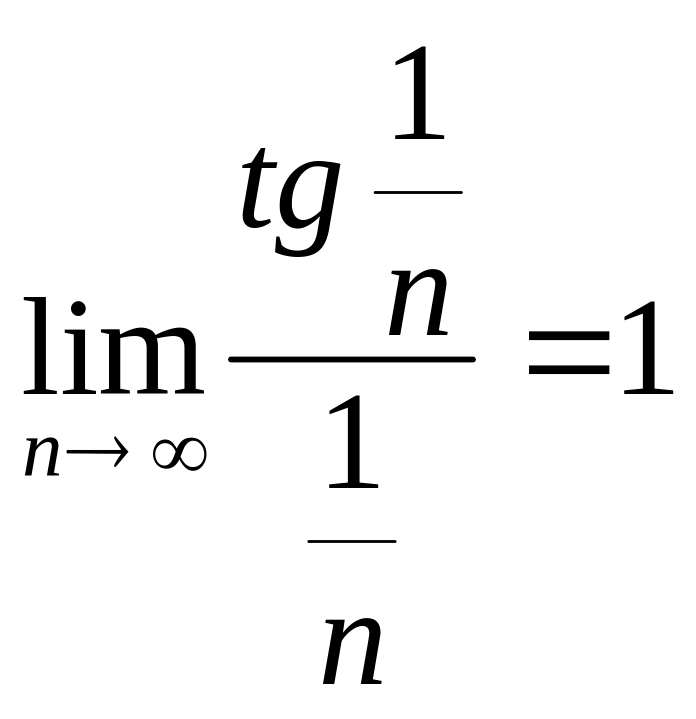Демек, берілген қатар жинақсыз.
11.6
Теорема (Д’Аламбер
белгісі).
Айталық,
қатары үшін
(11.8)
шегі бар болсын. Онда:
1º.
берілген қатар жинақты;
2º,
қатар жинақсыз.
11.7
Теорема (Коши
белгісі).
Айталық,
болғандағы
сандық қатары үшін
(11.9)
шегі бар болсын. Онда:
1º. қатар жинақты;
2º. қатар жинақсыз.
М.5*.
а)
;
ә)
қатарларын
жинақтылыққа зерттейік.
Шешуі. Д’аламбер белгісі бойынша тексерейік,
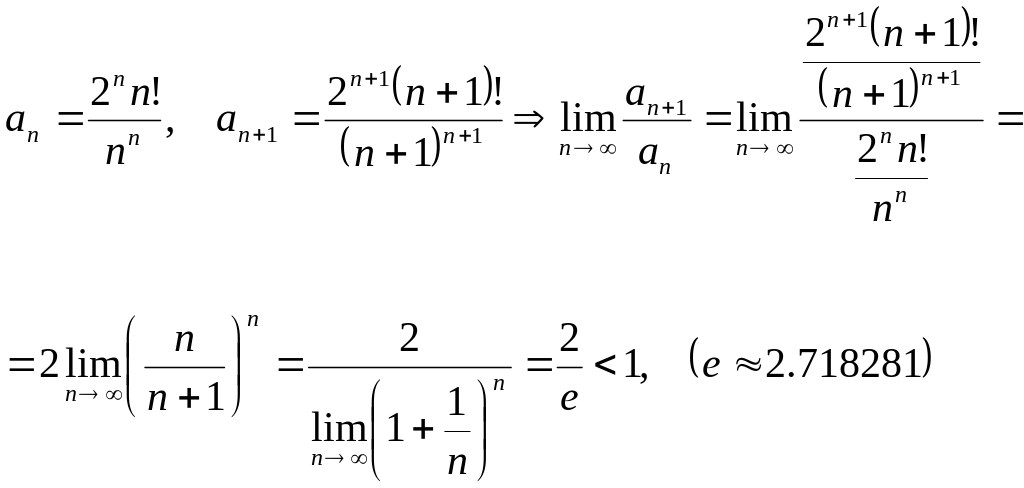
Демек, берілген қатар жинақты.
ә) Коши белгісін пайдаланайық,
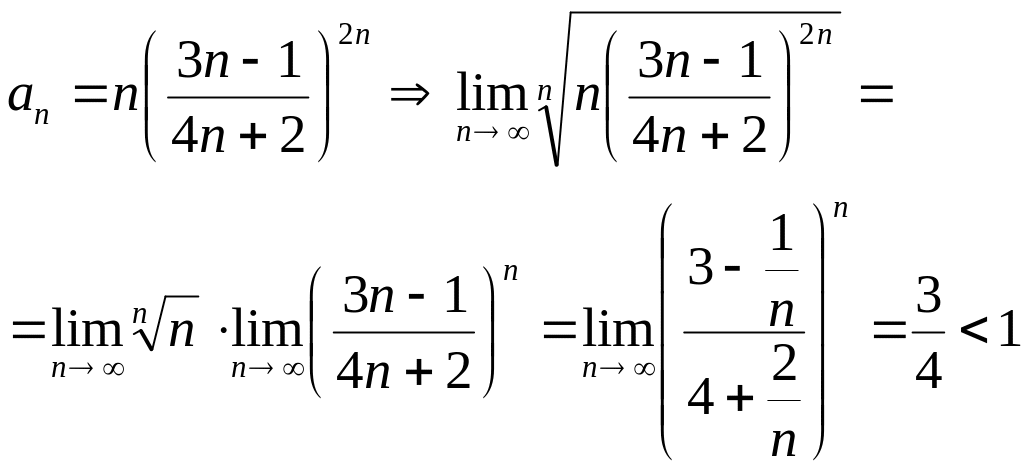
Ендеше, берілген қатар жинақты.
Ескерту.
Егер
,
болғанда,
зерттелетін қатар жинақты да, жинақсыз
да болуы мүмкін. Мысал үшін, гармоникалық
және бигармоникалық қатарлар үшін:
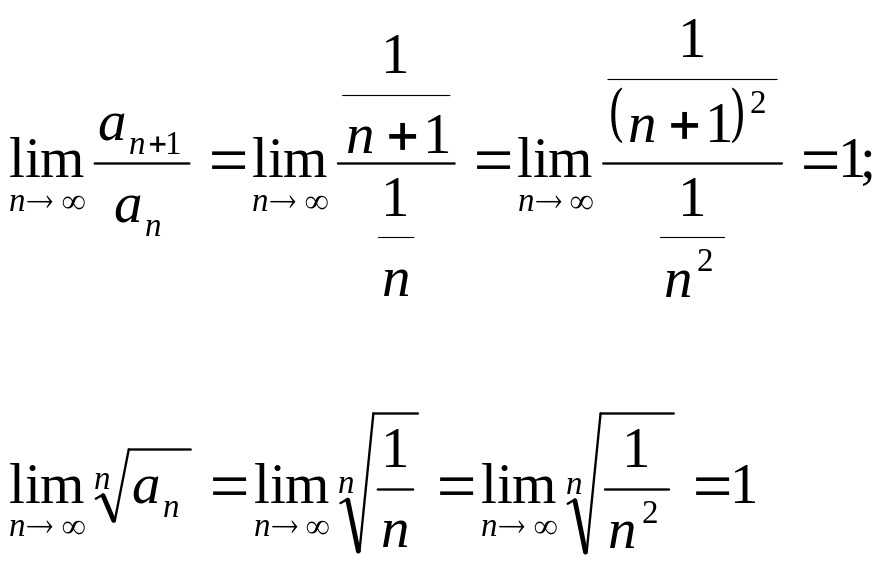
Ал,
─
гармоникалық қатардың жинақсыз.
─
бигармоникалық қатардың жинақты
болатындығы, жоғары да 3*-мысалда
көрсетілген.
11.8
Теорема (Коши
теоремасы).
Мүшелер
ара қатынаста болатын
қатарының жинақты болуы,
қатарының жинақты болуымен тікелей байланысты.
М.6*.
─
Дирихле қатарын жинақтылыққа зерттейік.
Шешуі.
Егер
болады
да, қатар жинақтылының қажетті шарты
орындалмайды. Демек,
болғанда Дирихле қатары жинақсыз.
Айталық,
болсын.
Енді көмекші
қатарын
қарастырайық, Егер
болса, (*) қатары, еселігі
болатын геометриялық прогрессияның
қосындысы болғандықтан, жинақсыз
болады. Ал
болғанда (*) қатары
болғандықтан, жинақты.
Сонымен,
соңғы 11.8 Коши теоремасы бойынша,
─
Дирихле қатары
болғанда жинақты және
болғанда жинақсыз болады.
М.7*.
қатарын жинақтылыққа зерттейік.
Шешуі.
Берілген қатарды
-дықтан,
мүшелері
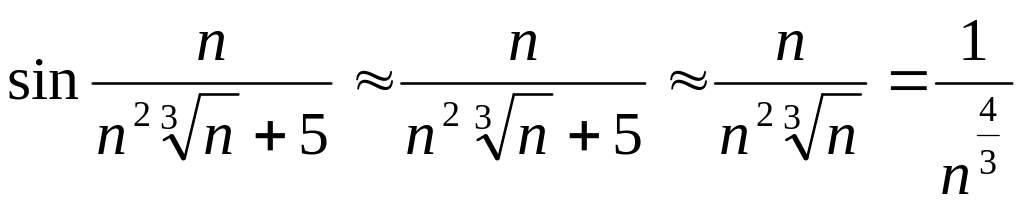
болатын қатармен салыстырудың шектік белгісімен (11.5 Т. ) салыстырамыз, яғни
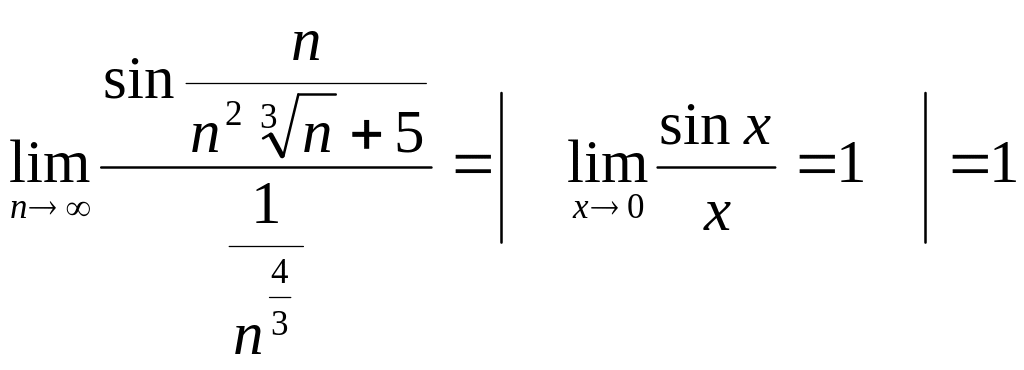
Демек,
─
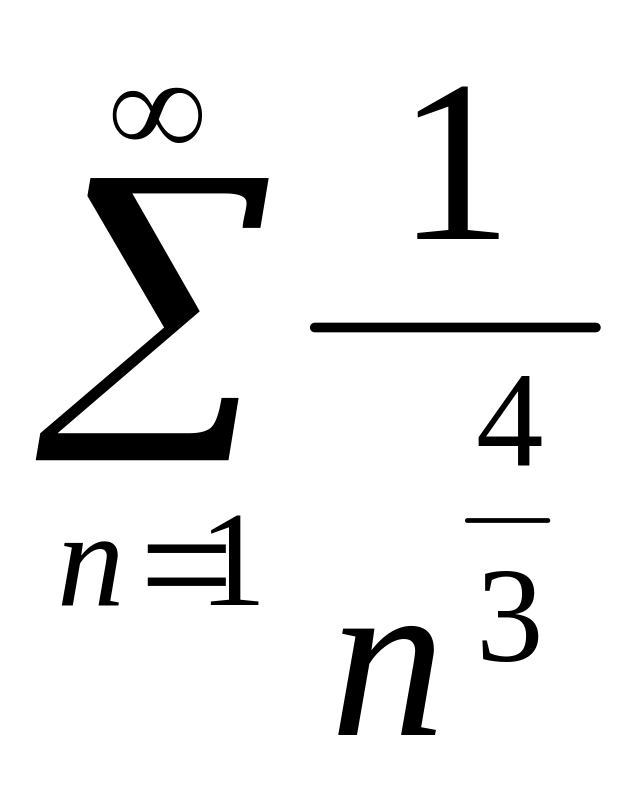Дирихле қатары
болғандықтан жинақты. Ендеше, берілген
қатар жинақты.
11.9
Теорема
(Коши-Маклореннің
интегралдық белгісі).
Айталық,
қатарының барлық мүшесін (көңілде ғана
(формально))
аралығында теріс болмайтын монотонды
функция ретінде қарастырайық. Онда
берілген
қатарының жинақты (я жинақсыз) болуы,
меншіксіз интегралының жинақты (я
жинақсыз) болуымен тікелей байланысты
болады.
М.8*.
қатарын жинақтылыққа зерттейік.
Шешуі.
Келтірілген Коши-Маклореннің интегралдық
белгісін бірден қолдансақ,
меншіксіз интегралын жинақтылыққа
зерттеуіміз қажет. Бірақ ол ауырлыққа
келтіретін болғандықтан,
үшін
(*)
Енді
берілген қатарды одан үлкенірек болатын
қатарымен салыстырамыз. Бұған
Коши-Маклореннің интегралдық белгісін
қолдану жеңіл. Сонымен,
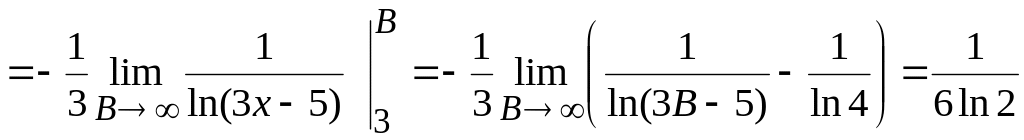
Демек, меншіксіз интеграл жинақты. Онда оған сәйкес қатары жинақты. Өз кезегінде, (*) ара қатынасты еске алсақ, жинақтылықтың салыстыру белгісі бойынша, берілген қатардың жинақтылықтылығы шығады.
М.9*.
қатарының қосындысын
-ге
дейінгі дәлдікпен табайық.
Шешуі.
болғандықтан, берілген қатарға сәйкес
қалдық қатар үшін алынған (11.10) бағаны
ескеру арқылы:
Бұдан
екендігі шығады. Ендеше,
