Побудова злачх розімкненої скоригованої сау
Для визначення коефіцієнта посилення
розімкненої системи будуємо на одній
площині ЗБЛАЧХ та ЗЛАЧХ не скоригованої
частини САР (рис. 24). Коефіцієнт
посилення розімкненої системи k,
визначається з рис. 24 як різниця між
ЗЛАЧХ не скоригованої частини та ЗБЛАЧХ
при частоті
.
Моментна складова похибки визначається рівнянням .
де
– струм короткого замикання в якірному
ланцюгу двигуна при номінальній напрузі,
що визначається рівнянням ,
– номінальна швидкість двигуна, яка
визначається рівнянням .
Швидкісна складова похибки системи визначається рівнянням .
Повна похибка системи визначається рівнянням .
Для перевірки того, що слідкуюча система задовольняє шуканим показникам точності скористаємося виразом та нерівністю (9.6). Слід зазначити, що в разі невиконання нерівності необхідно підвищувати значення коефіцієнту посилення системи.
Рис. 24. ЗБЛАЧХ та ЗЛАЧХ не скоригованої частини САР
Оскільки умова виконується але
,
то необхідно вводити послідовний
корегуючий пристрій (ПКП)
диференціально-інтегруючого типу .
,
при
.
Параметр
треба вибирати таким чином, щоб одержаний
після корекції результуючий
коефіцієнт
підсилення задовольняв умові:
.
Для ЗБЛАЧХ третього типу рекомендовано
обирати
;
для ЗБЛАЧХ другого типу рекомендовано
обирати
.
Для нашого прикладу приймаємо
та
Звідси
визначається рівнянням , а
рівнянням .
Після введення ПКП диференціально-інтегруючого типу передаточна функція ЗЛАЧХ незмінної частини прийме вигляд:
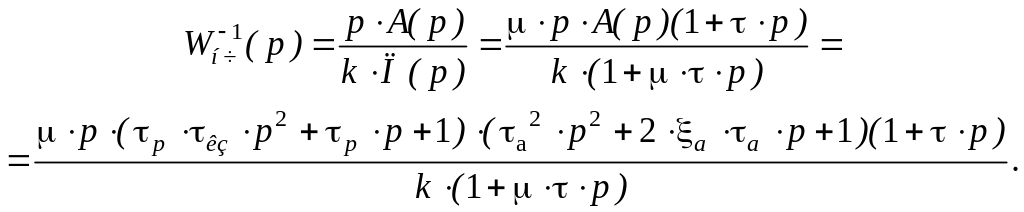
Отже, після частоти
нахил характеристики L|(jω)A(jω)|
зменшується на 1, а на частоті
- збільшується на 1.
Визначаємо спрягаючі частоти за рівняннями -.
Будуємо ЗЛАЧХ незмінної частини після введення ПКП диференціально-інтегруючого типу (ламана ABNLJX на рис. 24).
Визначаємо моментну складову похибки за рівнянням .
де
,
.
Швидкісна складова похибки системи визначається рівнянням .
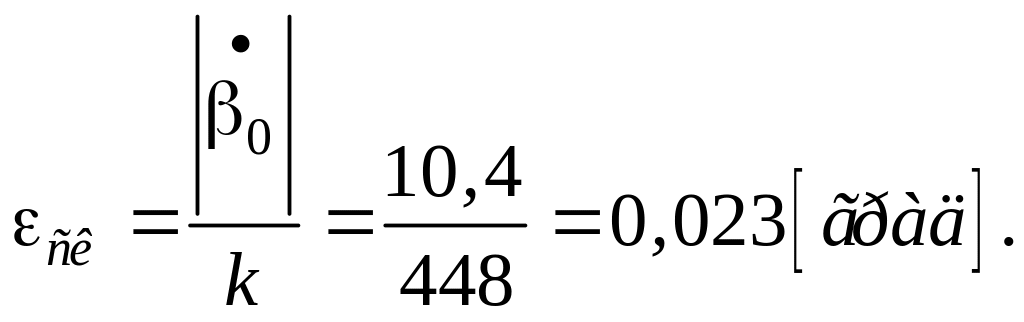
Повна похибка системи визначається рівнянням .
Як бачимо, розрахована сумарна похибка
системи менша за умовну та
,
що задовольняє умовам синтезу слідкуючої
системи.
Знайдемо мінімальне значення коефіцієнта
посилення
яке задовольняє умові
за рівнянням .
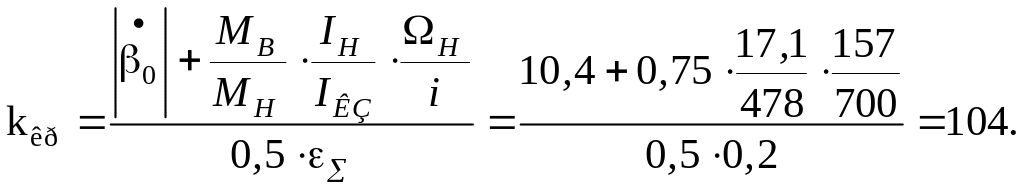
Зміщуємо отриману ЗЛАЧХ вниз до її
перетину з ЗБЛАЧХ при частоті
.
Та отримаємо ЗЛАЧХ розімкненої
скоригованої САУ (ламана AZFGHJX
на рис. 28). Значення частоти
має бути принаймні в 2 рази менше за
робочу частоту
[3, т., с.].
Згідно з рис. 24
.
Постійна часу
визначається за рівнянням .
На основі передаточної функції послідовного корегуючого пристрою вибираємо схему (рис. 25) послідовного корегуючого пристрою користуючись довідковою таблицею [2, с. 172-177].
Рис. 25. Схема послідовного корегуючого пристрою
Введемо заміну
,
та
.Передаточна
функція послідовно корегуючого пристрою
за рис. 25 має вигляд .
де
Задамось . Тоді елементи схеми (рис.8) визначаються за рівняннями -.
Після введення послідовного корегуючого пристрою принципова схема прийме вигляд (рис. 26).
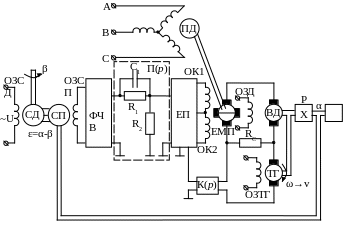
Рис. 26. Принципова схема слідкуючої САУ після введення послідовного корегуючого пристрою
Після синтезу послідовного коректуючого пристрою слід перевірити систему на точність шляхом визначення сумарної помилки та порівняння її із заданою . Має виконуватися нерівність та, відповідно, .
Рис. 27. ЗЛАЧХ після введення послідовного корегуючого пристрою
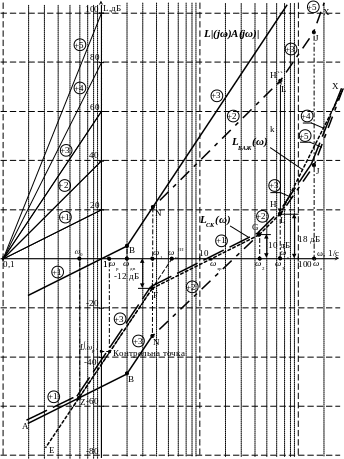
Рис. 28. ЗЛАЧХ розімкненої скоригованої САУ