Методические указания по выполнению задачи 1

К выполнению задачи 1 целесообразно приступить после изучения темы «Арифметические основы цифровой техники». Материал данной темы подробно освещен в [1, С. 72-92], [2, С. 151-166], [3, С. 9-19, 23‑34, 87-94].

Изучите правила и примеры, представленные в учебниках и данных методических указаниях. Затем приступайте к решению задачи 1.

Правила и примеры перевода чисел в десятичную систему счисления из двоичной и шестнадцатеричной систем счисления приведены в [1, С. 73], [2, С. 151, 152, 155, 156].

Рассмотрим пример перевода шестнадцатеричного числа A5F,C83 в десятичную систему счисления:

Правила и примеры перевода чисел в двоичную систему счисления из шестнадцатеричной приведены в [1, с. 75], [2, с. 154].

Рассмотрим пример:

Переводить десятичные числа в двоичную систему счисления можно различными способами. Наиболее простым является следующий расчетный метод:

Целую часть числа последовательно делят на два до тех пор, пока целая часть частного от последовательного деления станет равна 0. Результат перевода состоит из цифр остатков, причем последний остаток будет представлять старший разряд в записи целой части двоичного числа.

Дробную часть переводят путем последовательного умножения на два. Результат перевода дробной части получают из цифр целых частей частичных произведений, причем старшим разрядом является первая целая часть.

Целая часть числа переводится точно, дробная – приблизительно. Точность перевода дробной части зависит от числа знаков после запятой (см. [3, С. 14-19]).

Рассмотрим пример перевода десятичного числа 283,64 в двоичную систему счисления с точностью до семи знаков после запятой.

Переведем целую часть числа:

З апишем результат перевода целой части:

Переведем дробную часть числа, умножая последовательно на два только дробь, стоящую справа от запятой.

Запишем результат перевода дробной части:

Полный результат перевода:

Правила представления и суммирования двоичных чисел в дополнительном коде приведены в [3], С. 30-33, 81-87]. Перед решением пункта 3 задачи 1 изучите теоретический материал и примеры, приведенные в данных методических указаниях.

Дополнительный код отрицательного двоичного числа находится как дополнения модуля этого числа до граничного числа, представляемого в данной разрядной сетке. Дополнительный код для двоичных чисел меньших единицы образуется по формуле:

где –граничное число, причем .

Рассмотрим примеры:

= + 0,1101;

= – 0,1101;

Из формулы и примеров видно, что изображение положительного числа в дополнительном коде совпадает с его изображением в прямом коде. Для представления отрицательного двоичного числа в дополнительном коде необходимо в знаковом разряде поставить единицу, произвести замену цифр исходного числа на обратные и к полученному коду прибавить единицу младшего разряда.

Обратное преобразование, т.е. получение числа из дополнительного кода выполняется по тому же правилу, что и получение дополнительного кода. Рассмотрим пример:

При алгебраическом сложении двоичных чисел в дополнительном коде используются следующие правила:

а) знаковые разряды суммируются так же, как и значащие разряды числа;

б) единица переноса из знакового разряда при сложении в дополнительном коде отбрасывается;

в) если в знаковом разряде суммы получился нуль, то сумма положительна и для перехода к естественной форме числа обратное преобразование не требуется. Если же в знаковом разряде суммы получилась единица, то сумма отрицательна и требуется обратное преобразование.

Рассмотрим примеры.

Пример 1

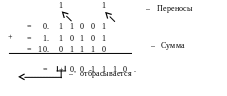Выполним суммирование двух двоичных чисел X₁ = + 0,11001 и X₂ = – 0,01011 в дополнительном коде.

Результат получился положительным, и обратное преобразование не требуется.

Пример 2

Поменяем знаки чисел и и выполним суммирование в дополнительном коде. Результат получится отрицательным, и потребуется обратное преобразование.

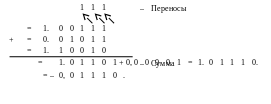При сложении чисел одного знака может произойти переполнение разрядной сетки, что приведет к искажению результата. На практике для выявления переполнения разрядной сетки применяют модифицированные машинные коды, в которых два знаковых разряда. Для положительных чисел в знаковых разрядах записывается 00, для отрицательных – 11. Появление комбинаций 01 или 10 в знаковых разрядах свидетельствует о переполнении разрядной сетки, т.е. является сигналом ошибки. Например, двоичное число X = – 0,1101 в модифицированном дополнительном коде будет записано следующим образом:

= 11.0011.

Пример 3

Выполним суммирование двух десятичных чисел  = + 0,450 и  = – 0,575 в двоичной СС с точностью до пяти знаков после запятой в дополнительном модифицированном коде и сравним результаты суммирования в двоичной и десятичной СС.

Т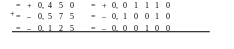 ак как |   | > |   |, то в естественной форме следует выполнить вычитание числа X₁ из числа X₂ и результату присвоить знак минус.

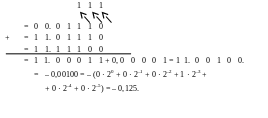
Результаты суммирования в естественной форме и дополнительном модифицированном коде совпадают.

Правило и пример перевода десятичного числа в двоично-десятичный код 8421 приведены в [1, С. 73, 74] и [5, С. 19, 20].

Рассмотрим пример:

Правило и примеры суммирования десятичных чисел в коде 8421 приведены в [1, С. 85, 86], [2, С. 165], [3, С. 91, 92].

Рассмотрим пример суммирования десятичных чисел  = 458 и  = 629 в десятичной СС и коде 8421.

Десятичная система счисления:

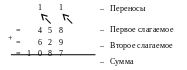
Код 8421:

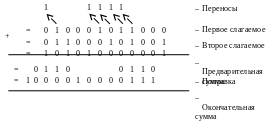
В младшей тетраде коррекция проведена из-за наличия единицы переноса во вторую тетраду.

Результаты суммирования в десятичной и двоично-десятич­ной системах счисления совпадают.