УДК 519.17 Инв. № ___ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ Национальный аэрокосмический университет им. Н. Е. Жуковского «ХАИ» Кафедра 304 ОБРАБОТКА РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ пояснительная записка к расчетно-графическому заданию по дисциплине «Основы информационных технологий и программирования» Выполнил студент гр. 212 И. И. Иванов «____»_______201_ г. (подпись, дата) Проверил к.т.н., доцент Ю. А. Скоб «____»_______201_ г. 2014

Расчетно-графическая работа №2

ОБРАБОТКА РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ

Цель – закрепить навыки разработки графического приложения Fortran для решения простейших инженерных задач; освоить приемы работы с выводом графика нескольких функций; изучить основы применения численной аппроксимации таблично заданных функций методом наименьших квадратов и решения систем линейных алгебраических уравнений методом исключений Гаусса.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Аппроксимация данных методом наименьших квадратов

Пусть в результате эксперимента получена таблица значений функции:

X	x0	x1	x2	…	xn
Y	y0	y1	y2	…	yn

Требуется аппроксимировать эту функцию многочленом степени m (m<n):

.

Согласно методу наименьших квадратов (МНК) ищем значения параметров , при которых сумма квадратов

принимает минимальное значение.

С учетом необходимых условий существования экстремума функции нескольких переменных получаем систему уравнений для определения неизвестных :

Доказано, что система уравнений имеет единственное решение, при котором принимает минимальное значение.

Рассмотрим частные случаи.

Случай 1. Пусть , т.е. функцию аппроксимируем многочленом первой степени:

.

Система уравнений для вычисления параметров , имеет следующий вид:

Решив систему, можем записать требуемый многочлен .

Случай 2. Пусть , т.е. функцию аппроксимируем многочленом второй степени:

.

Система уравнений для определения параметров имеет следующий вид:

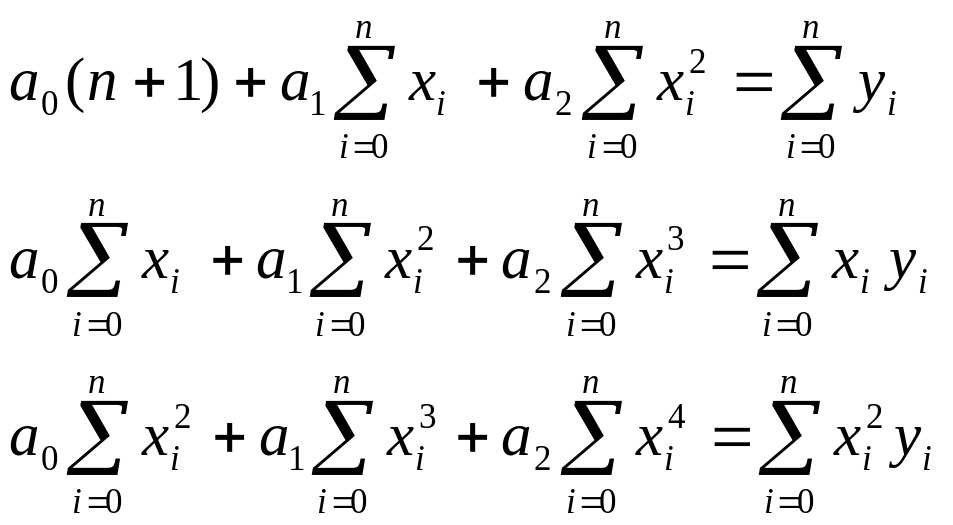
Решив систему, можно записать многочлен .

Решение системы линейных алгебраических уравнений методом Гаусса

Представим исходную систему линейных алгебраических уравнений (СЛАУ) в виде

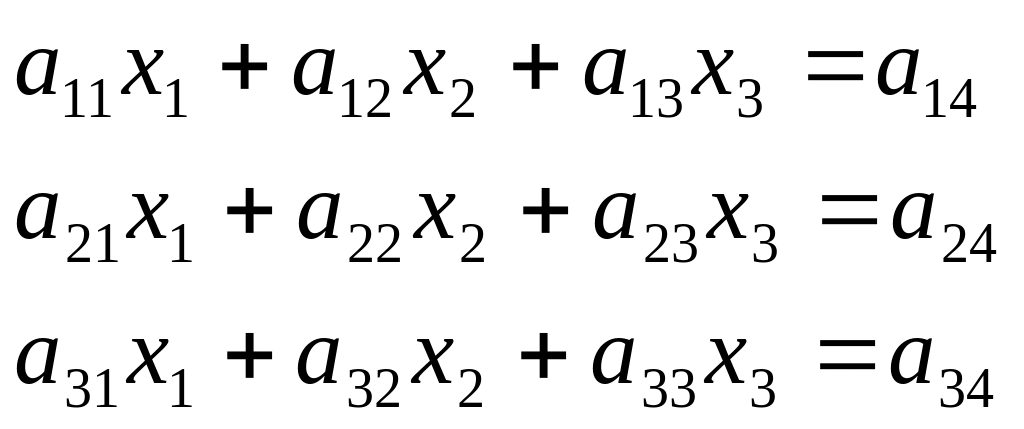(1)

Делим первое уравнение системы (1) на . В результате получим уравнение

, (2)

где .

Из второго уравнения системы (1) вычитаем уравнение (2), умноженное на , а из третьего уравнения системы (1) – уравнение (2), умноженное на . Получаем систему

(3)

где .

Делим первое уравнение системы (3) на . В результате получим уравнение

, (4)

где .

Умножая уравнение (4) на и вычитая его из второго уравнения системы (3), получаем:

, (5)

где .

Наконец, разделив уравнение (5) на , получим:

, (6)

Используя уравнения (4) и (2), находим последовательно и .

Вариант задания

№ вари­анта	Исходные данные
6	x	-1	0	1	2	3	4	5
	y	3,1	2,8	2,4	2,1	1,9	2,2	2,6

Требуется методом наименьших квадратов найти многочлены первой и второй степеней, аппроксимирующие заданную функцию.

ВЫПОЛНЕНИЕ ВАРИАНТА

1. Текстовый файл DZ_V1.txt .

2. Результаты аппроксимации таблично заданной функции с помощью метода наименьших квадратов. Кривая параболы должна более качественно и точнее отвечать процессу, представленному таблично заданной функцией.

ПРИЛОЖЕНИЕ 1