Лабораторная работа № 14

ОПРЕДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКИХ ТРАНСЦЕНДЕНТНЫХ

УРАВНЕНИЙ МЕТОДОМ ПОЛОВИННОГО ДЕЛЕНИЯ

Цель работы – освоить навыки приближенного нахождения корней алгебраических трансцендентных уравнений методом половинного деления в различных средах программирования; научиться реализовывать вычислительный процесс с помощью приложения Windows диалогового типа

Постановка задачи:

Используя метод половинного деления, вычислить с заданной точностью ( 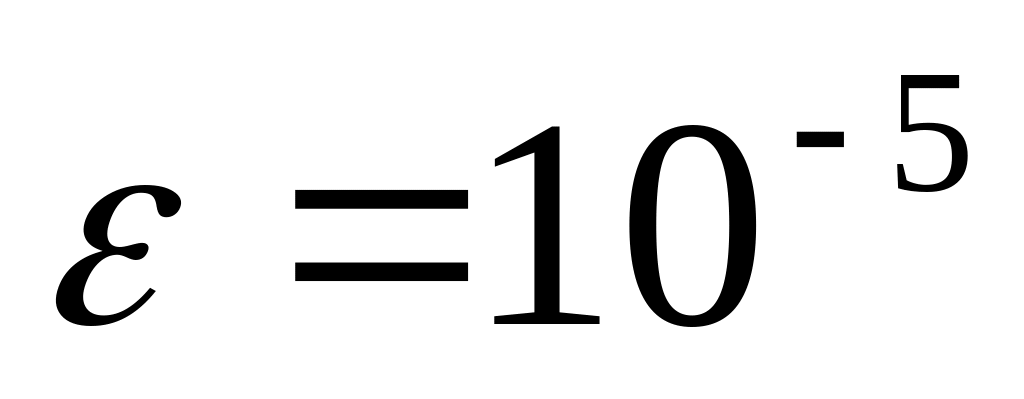) действительные корни заданного алгебраического уравнения .
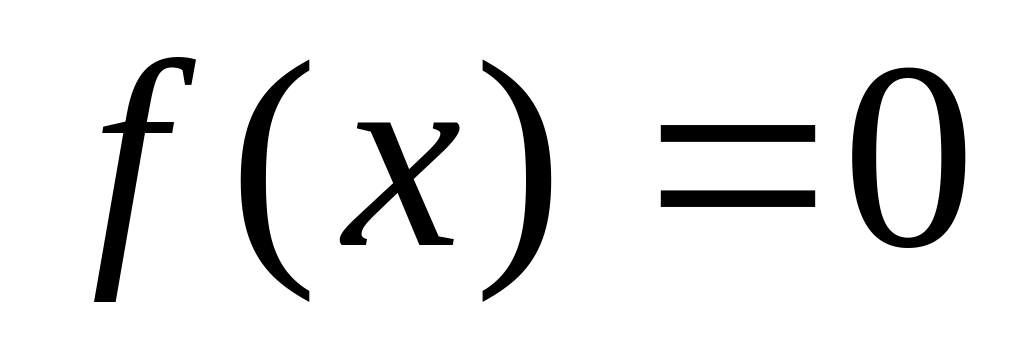Решить задачу в различных средах: Fortran, MS Excel и MathCad.

Теоретические сведения

1. Отделение действительных корней. Рассмотрим уравнение . Для отделения корней можно использовать следующую теорему: если непрерывная функция принимает значения разных знаков на концах отрезка , т.е. , то внутри этого отрезка находится, по крайней мере, один корень уравнения .

Отделение корней происходит так. Находим знаки функции в ряде точек из области определения функции , , , … . Если , то в силу сформулированной выше теоремы на отрезке имеется, по крайней мере, один корень уравнения . Необходимо одним из способов проверить, является ли этот корень единственным. Если на отрезке не меняет знак, корень - единственный (в силу монотонности ).

Для отделения корней можно использовать графические методы. Строим график функции и по чертежу находим интервалы, содержащие точки пересечения графика с осью , т.е. корни уравнения . Иногда уравнение удобно представить в виде и, построив графики функций и , определить интервалы, содержащие точки их пересечения.

Пример. Отделить корни уравнения .

Способ 1. Определяем знаки функции в ряде точек (таблица):

	-3	-2	-1	0	1	2	3
	-	-	+	+	+	-	+

Найдены три отрезка, на концах которых функция имеет разные знаки: , , .

Алгебраическое уравнение третьей степени имеет три корня. Следовательно, каждый из трёх указанных отрезков содержит один корень уравнения.

2. Метод половинного деления. Пусть найден отрезок , на котором находится единственный корень уравнения . Обозначим его . Для нахождения корня уравнения делим отрезок пополам. Если , то и задача решена. В случае выбираем ту половину отрезка , на концах которой функция имеет противоположные знаки. Новый суженный отрезок снова делим пополам, повторяем те же действия и т.д. В результате на каком-то этапе получаем точный корень уравнения или последовательность вложенных друг в друга отрезков , ,…, ,… . Доказано, что . Для вычисления корня уравнения с точностью до , отрезок делим до тех пор, пока выполнится условие . За приближённое значение корня берём среднюю точность отрезка :