Пример. Фирма может принять решение о строительстве крупного или

мелкого предприятия. Строительство крупного предприятия относительно

дешевле, в случае если будет высокий спрос на производимые товары, мел-

кое предприятие можно расширить. Деятельность фирмы рассматривается в

течение десяти лет, причём в случае строительства мелкого предприятия во-

прос о расширении будет рассматриваться через два года. Спрос заранее не-

известен.

p=0,75

1,0

крупное

2

p=0,25

0,3

1

мелкое

3

p=0,75

4

расш

без расш.

5

6

p=0,75

p=0,25

p=0,75

p=0,25

0,9

0,2

0,25

0,2

2 года

p=0,25

8 лет

0,2

Рис. 67

Введём градацию случайного спроса: высокий (p>0,75) и низкий

(p<0,25). Затраты и доходы: строительство крупного предприятия - 5 млн. $;

строительство мелкого - 1 млн. $; затраты на расширение - 4,2 млн. $; круп-

ное предприятие при высоком спросе даёт доход - 1 млн. $ ежегодно, а при

низком - 300 тыс. $; мелкое предприятие при высоком спросе - 250 тыс. $

ежегодно, при низком - 200 тыс. $; расширенное предприятие в случае высо-

кого спроса приносит доход - 900 тыс. $ в год, и при низком спросе - 200

тыс. $; мелкое предприятие без расширения при высоком спросе на произво-

димый продукт приносит в течение двух лет по 250 тыс. $ ежегодно, а в те-

чение следующих восьми по 200 тыс. $. Нарисуем дерево решений.

Применим для решения этой задачи метод динамического программиро-

вания. В качестве критерия применим средний выигрыш, т. е. МО выигрыша.

Сама величина критерия равна доходу без затрат на строительство. Начнём с

последнего четвёртого шага, подсчитаем средний выигрыш:

166

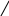
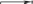
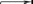
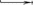
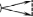
4

4

1

1

Исходя из полученного результата, оптимальным будет сразу строить

крупное предприятие.

Другим примером оптимизации многоэтапных операций является из-

вестная «задача о секретарше».

Директор собирается принять на работу секретаршу. Прежний опыт де-

лит секретарш на три категории: отличных (3 балла), хороших (2 балла) и

посредственных (1 балл). Анализ учебных заведений по подготовке секре-

тарш даёт статистику выпускниц заведений: вероятность взять на работу от-

личную секретаршу - 0,2, хорошую - 0,5, посредственную - 0,3. директор

может испытать только трёх претенденток, причём в случае отказа директора

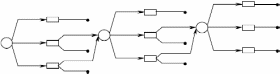
кандидат убывает на другую работу. Построим дерево решений.

p=0,2

stop

1

p=0,2

p=0,3

p=0,5

stop

a=3

пр о до лжить

stop

a=1

пр о до лжить

stop

a=2

2

p=0,2

p=0,3

p=0,5

stop

a=3

пр о до лжить

stop

a=1

пр о до лжить

stop

a=2

3

p=0,3

p=0,5

stop

stop

Рис. 68

В соответствии с процедурой динамического программирования начнём

искать оптимальное решение с последнего шага. Определим математическое

ожидание «выигрыша», если мы испытываем третьего кандидата:

a3 3*0, 2 2*0,5 1*0,3 1,9 .

Далее определим средний выигрыш, если мы испытываем второго и

третьего, с учетом того, что если второй будет посредственный, то мы про-

должим и получим в среднем 1.9.

a2 3*0, 2 2*0,5 1,9* 0,3 2,17 .

167

a расш 0,9 * 0,75 0, 2 * 0, 25 *8− 4, 2 1,6 ,

aбез расш 0, 25* 0,75 0, 2 * 0, 25 *8 1,9 ,

aкруп1* 0,75 0,3* 0, 25 *10− 5,0 3, 25 ,

aмелк1,9 2 * 0, 25 * 0,75 0, 2 *10 * 0, 25 1,3 .

Поэтому если во втором испытании попалась хорошая секретарша, надо

остановиться, т.к. получим 2, а если продолжим, то только 1.9.

При первом испытании, надо остановиться, только если попалась отлич-

ная, а в третьем испытании берём любую. Найдём средний оптимальный вы-

игрыш при оптимальном правиле испытания трех кандидатов:

a1 3*0,2 2,17 *0,5 2,17 *0,3 2,336 .

Следовательно, за счет возможности испытывать трех секретарш мы по-

лучаем дополнительный выигрыш 2,336 – 1,9 = 0,436.

168

10. Экспертные процедуры

ДЛЯ ПРИНЯТИЯ РЕШЕНИЙ

В практических задачах принятия оптимального решения альтернативы

не являются «математическими объектами», а чаще представляют собой кон-

кретные физические системы: продукты, технологии, организация техниче-

ского мероприятия, системы и т.д. Для описания альтернатив и оценки по-

следствий их принятия необходимо решить следующие задачи:

– построить множество возможных и допустимых альтернатив;

– сформировать набор аспектов, существенных для оценки альтернатив;

– определить критериальное пространство;

– упорядочить альтернативы по аспектам;

– получить оценку альтернатив по критериям, то есть найти отображение

Ω в критериальное пространство (см. главу 7).

Все эти задачи являются модификацией общей задачи оценивания: со-

поставление числа или нескольких чисел рассматриваемой альтернативе.

Методы решения задачи оценивания основаны на использовании экс-

пертных процедур, поэтому их называют методами экспертных оценок.

10.1. Общая схема экспертизы

В общем случае из-за сложности оценивания систем привлекаются люди

– специалисты в данной предметной области – эксперты. Решение задач оце-

нивания называют э к с п е р т и з о й. Вопросы, связанные с экспертизой, рассмат-

риваются и решаются к о н су л ь т а н т о м. Он определяет Ω, а иногда и вспомога-

тельное множество для экспертизы Ωэ и организует всю процедуру эксперти-

зы.

1. Консультант находит множество допустимых оценок Ω, в которых

содержится исходная оценка.

2. Он определяет множество допустимых оценок Ωэ, из которого осу-

ществляют выбор эксперты.

3. Каждый эксперт выбирает свою оценку ai Ci (Ωэ), i= 1, N . При этом

эксперты могут взаимодействовать между собой.

4. По заранее разработанному алгоритму (формуле) консультант произво-

дит обработку полученной от экспертов информации и находит результирующую

оценку, являющуюся решением исходной задачи оценивания.

5. Если полученное решение не устраивает консультанта, то он предос-

тавляет экспертам дополнительную информацию, то есть организует обрат-

Отформат

Отступ: Сл

строка: 14

нумерованн

+ Стиль ну

… + Начать

Выравнива

Выровнять

Табуляция

Отступ: 36

Поз.табуля

Выровнять

табуляции

ную связь, после чего они вновь решают задачу оценивания.

169

10.2. Задача оценивания

Смысл оценивания состоит в сопоставлении альтернативе вектора из Еm.

Перечислим типичные варианты этой задачи:

1.

2.

Пусть X∈ – альтернатива в задаче принятия решений. Имеются m кри-

териев. Требуется альтернативе X∈ сопоставить вектор

[f1(x),f(x),…fm(x)]∈Еm.

Пусть k1, k2, …, km – критерии, учитывающиеся при выборе. Их необхо-

димо упорядочить по важности. Тогда системе S=(k1, k2, …, km) сопостав-

ляется перестановке натуральных чисел от 1 до m, i1,…im ,где ik – номер

k-ого критерия при упорядочивании по важности.

Отформ

ширине,

Уровень:

нумераци

Начать с

Выравни

Выровня

Табуляци

Отступ:

3.

Пусть множество D разбито на l подмножеств D1, D2, …, Dl. Для эле-

мента х∈ D необходимо указать, к какому из подмножеств Di (i =1, l ) он

относится. То есть х сопоставляется одно из чисел от 1 до l. Пусть х от-

резок, длину которого надо измерить. То есть отрезку надо сопоставить

действительное число; f(x) – длина отрезка.

Отформ

ширине,

Уровень:

нумераци

Начать с

Выравни

Выровня

Задача №1 – это общая задача м н о г о к р и т е р и а л ь н о й о ц е н к и.

Задача №2 – это задача ранжирования.

Табуляци

Отступ:

Задача №3 – это задача к л ас с и ф и к а ц и и.

Задача №4 – это обычная задача и з м е р е н и я.

Обозначим Ω – исходное множество допустимых значений оценок

(МДО).

Ωэ - МДО для экспертов;

L – взаимодействие между экспертами;

Q – обратная связь;

N

Назовем схемой экспертизы пятерку параметров (Ω,Ωэ,L,Q,φ).

Подготовка экспертизы – это предварительная разработка схем

экспер-

тизы и подбор экспертов.

Реализация экспертизы – получение от экспертов информации и её обра-

ботка.