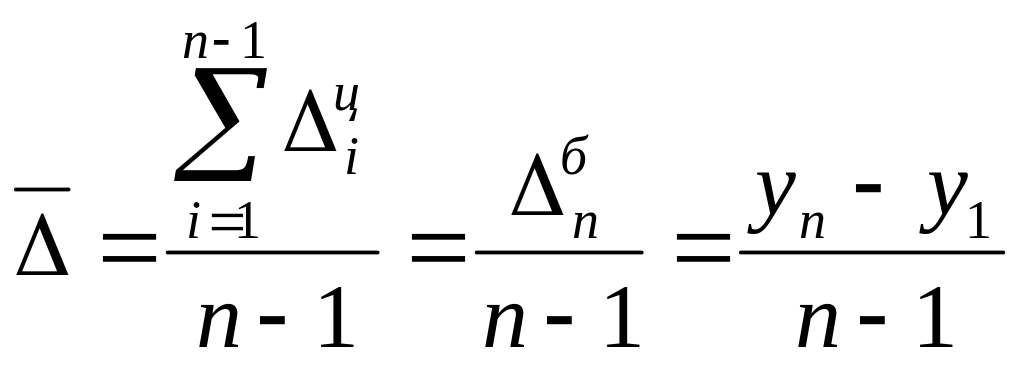9.3.3. Средние показатели изменения уровней ряда

Для обобщающей характеристики динамики исследуемого явления в целом за анализируемый период определяют средние показатели изменения уровней ряда: средний абсолютный прирост, средние коэффициенты (или темпы) роста и прироста, среднее абсолютное значение одного процента прироста. Средние показатели изменения уровней ряда рассчитываются как на основе цепных, так и на основе базисных показателей изменения уровней ряда.

Средний абсолютный прирост рассчитывается как средняя арифметическая из цепных абсолютных приростов ряда:

(9.21)

Для динамического ряда численности населения РФ за 2003 – 2007 годы, приведенного в таблице 9.11, средний абсолютный прирост численности населения равен млн. человек в год.

Средний коэффициент роста вычисляется по формуле средней геометрической из цепных коэффициентов роста ряда:

(9.22)

Средний коэффициент роста показывает, во сколько раз в среднем за единицу времени изменялись уровни динамического ряда.

Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах.

(9.23)

Средние коэффициент и темп роста являются обобщенными показателями интенсивности развития явления за длительный период времени, поэтому имеют важное значение при выявлении и описании долговременной тенденции развития.

По данным о динамике среднемесячной номинальной начисленной заработной платы работающих в РФ за 2002-2007 годы, приведенные в таблице 9.12, средний коэффициент роста среднемесячной зарплаты в год равен , а средний темп роста составляет 125,4% в год.

Средние коэффициент и темп прироста рассчитываются на основе средних коэффициента и темпа роста:

	(9.24)
	(9.25)

Средний темп прироста показывает, на сколько процентов в среднем за единицу времени изменялись уровни динамического ряда.

Средний коэффициент прироста среднемесячной номинальной начисленной заработной платы работающих в год а течение анализируемого периода составил , а средний темп прироста составляет 25,4% в год.

Среднее абсолютное значение одного процента прироста можно рассчитать по формуле:

(9.26)

На практике применение средних показателей изменения уровней ряда позволяет получить хорошие результаты в случае более или менее постоянного изменения уровней. В случае сильной колеблемости уровней ряда использование средних показателей может дать искаженное представление о средней интенсивности изменения уровней ряда. В таких случаях предлагается рассчитывать средние коэффициент роста и прироста после некоторого предварительного преобразования динамического ряда (например, выравнивание уровней).

Особую осторожность при применении средних абсолютных приростов или средних темпов роста (прироста) следует соблюдать в тех случаях, когда в ряду наблюдается резкое изменение существующей тенденции развития признака. В этом случае средние показатели изменения уровней ряда не будут информативными.