Курсовая работа по механике

Омский Государственный Технический Университет

Кафедра «Сопротивление материалов»

Курсовая работа по механике

Расчет плоских ферм

Выполнил:

ст. гр. Э-236

Мельникова Н.А.

Проверил

доцент

Подколзин Г.П.

Омск 2007.

Рассчитаем ферму, изображенную на рисунке 1.

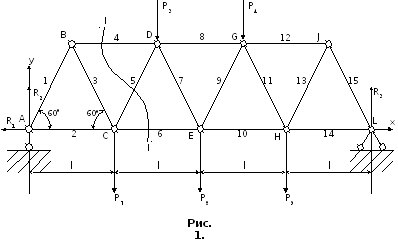
Все стержни имеют длину l = 1,6 м. Силы, действующие в узлах D, G, C, E и Н из­вестны: P₃=100 кН, P₄=160 кН, P₇=120 кН, P₈=P₉=50 кН. Материал стержней – сталь с расчетным сопро­тивлением R = 200 МПа. Коэффициент условий работы стержней =0,75.

Определим продольные силы в стержнях 4, 5 и 6 и подберем сечение в виде равно­полочного уголка для наиболее нагруженного сжатого стержня из рассчитываемых стержней.

1. Проверка геометрической неизменяемости и статической определимости фермы.

В рассматриваемой ферме число стержней S = 15, а число узлов K = 9. Проверим геометрическую неизменяемость и статическую определимость фермы по условию ():

.

Условие выполняется, т.е. ферма геометрически неизменяема и статически опреде­лима.

2. Определение реакций опор.

Под действием внешних активных и реактивных сил ферма находится в равнове­сии. Составим уравнения равновесия для определения неизвестных реактивных сил.

Вначале составим уравнение в виде суммы моментов всех внешних сил относи­тельно узла А:

.

Тогда реактивная сила R₃ равна:

Составим уравнения равновесия в виде сумм проекций всех внешних сил на оси ху:

откуда:

Итак, R₁=0, R₂=480 кН, R₃=250 кН.

3. Определение продольных сил в стержнях 4,5,6.

Для определения продольных сил в стержнях 4,5, и 6 рассечем ферму так, чтобы в сечение попадали эти стержни (линия I – I на рис. 1). Разрезав таким образом ферму на две части, одну из них отбросим и рассмотрим условия равновесия той части, ко­торая имеет меньшее количество узлов. В данном случае – левую часть. Она остается в равновесии под действием внешних сил R₁, R₂, P₇ и внутренних продольных сил N₄, N₅, N₆ в рассеченных стержнях, которые заменяют действие отброшенной правой части фермы. Вначале считаем продольные силы растягивающими.

Продольную силу N₄ определим из уравнения равновесия в виде суммы моментов всех сил относительно узла С:

откуда,

.

Плечо продольной силы N₄ h=lcos30⁰. Тогда:

­­

Из полученного результата следует, что в действительности сила N₄ направлена к сечению, т.е. она сжимающая.

Продольную силу N₅ определим из уравнения равновесия в виде суммы проекций всех сил на ось y (рис. 1.1.).

откуда,

.

Из полученного результата следует что сила N₅ в действительности направлена к узлу С от сечения.

Продольную силу N₆ определим из уравнения в виде суммы моментов всех сил от­носительно точки D:

учитывая, что h=lcos30⁰, находим:

.

4. Подбор сечения сжатого стержня фермы из расчета на устойчивость

Первое приближение

­­

Принимаем и находим требуемую площадь поперечного сечения сжатого стержня N₆ по формуле .

По ГОСТ 8509-86 принимаем равнополочный уголок с площадью поперечного сечения и минимальным радиусом инерции. Гибкость стержня

.

Для данного расчетного сопротивления находим:

Определим величину погрешности в определении коэффициента продольного изгиба в первом приближении:

Погрешность превышает допустимую величину. Необходимо второе приближение.

Второе приближение

Требуемая площадь поперечного сечения стержня

По ГОСТ 8509-86 принимаем равнополочный уголок с площадью поперечного сечения и минимальным радиусом инерции. Гибкость стержня

.

Для данного расчетного сопротивления находим:

Определим величину погрешности в определении коэффициента изгиба во втором приближении:

Погрешность превышает допустимую величину, необходимо третье приближение.

Третье приближение

Требуемая площадь поперечного сечения стержня

По ГОСТ 8509-86 принимаем равнополочный уголок с площадью поперечного сечения и минимальным радиусом инерции. Гибкость стержня

.

Для данного расчетного сопротивления находим:

Определим величину погрешности в определении коэффициента изгиба в третьем приближении:

Поскольку погрешность не превышает допустимой величины, на этом расчеты можно закончить.

Убедимся в том, что подобранное сечение удовлетворяет условию устойчивости:

;

;

Условие устойчивости выполняется.

Итак, принимаем по ГОСТ 8509-86 равнополочный уголок №20 с площадью поперечного сечения .