8.6. Транспортна задача у сітьовій постановці

Транспортну задачу можна зобразити графом, на якому кожна дуга має значення , та кожна вершина – значення зі знаком „+” або зі знаком „-”.

Транспортна задача у сітьовій постановці відображається такою математичною моделлю:

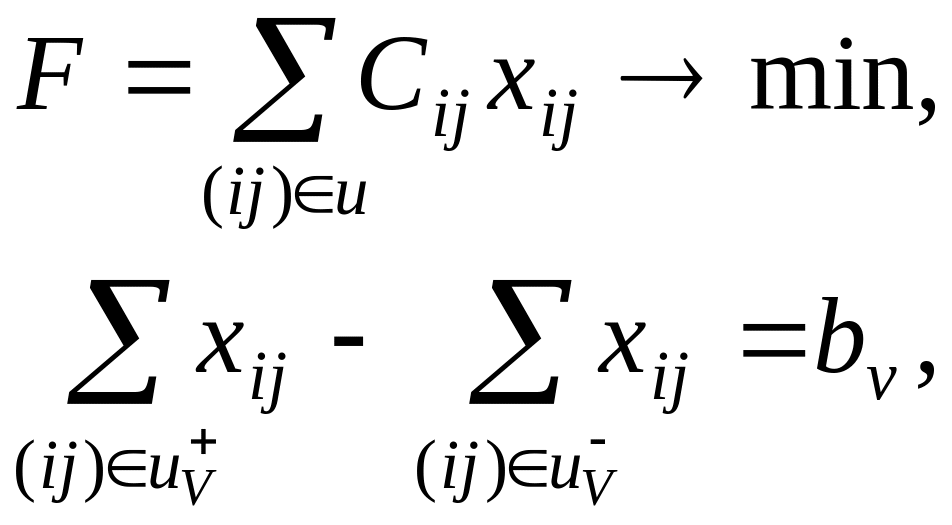
де – потужність постачальника або попит споживача; – множина дуг, які входять до вершини ; – множина дуг, які виходять з вершини ; – множина дуг графа .

Напрямок переміщування вантажу вказується дугою. До графу також входять вершини, які не відображують постачальника чи споживача; такі вершини є проміжними з нульовими запасами чи потребами (так звані перевалочні бази).

Для знаходження оптимального варіанта згідно з графом транспортної задачі будується який-небудь перший розв’язок цієї задачі з урахуванням ребер неорієнтовного графа та значень . Таким чином, між пуктами, де йде переміщення вантажу, ребро графа має значення . Знаходження оцінки кожного ребра ведеться як

, де .

Якщо для усіх ребер графа , то план розвязку є оптимальним.

Розміщення значень та за вершинами здійснюється так. Вибирається для однієї з вершин постачальника довільне значення и. Потім згідно з напрямком дуг і величин знаходяться значення для інших вершин, як , де знаки „+” або „-” відповідають обходу за напрямком чи протилежно напрямку дуг відповідно.

Якщо план довільний , то знаходяться значення для ребер графа (без напрямку), а для ребер з будується цикл з дугою від до і. Потім вибирають усі протилежні дуги і з них знаходиться величина , яка і буде відповідати значенню перевезення вантажу від до і. Це ребро доповнюється стрілкою-дугою. Дуга з мінімальним значенням постачання ліквідується, залишається тільки ребро між цими вершинами. Величина додається до значень усіх дуг цього напрямку та віднімається від дуг протилежного напрямку.

Приклад. Нехай є транспортна задача у сітьовій постановці (рис. 8.11).

4 3

3 2

1

Рис.8.11

Перший базисний розв’язок має вигляд (рис. 8.12).

15 10

10 4 3 12

40 3 2

1 20

20 20

Рис.8.12

Перевірка:

, тобто не є оптимальним.

Для ребра (14) будується дуга(14), потім для неї знаходиться цикл (1, 4, 2, 5, 3) та обчислюється з дуг протилежного напрямку.

Дузі (14) надається значення : дуга (12) ліквідується (як з мінімальним значенням ) та залишається тільки ребро між вершинами 2 та 4. Потім знаходиться решта згідно з напрямком дуг:

Будується новий план розподілу ресурсів (рис. 8.13).

10 14

10 4 3

12

30

1 30

10

14

Рис.8.13

варіант є оптимальним.