7.2.2. Перший алгоритм Гоморі

Алгоритм розв’язування передбачає знаходження оптимального розв’язку повністю цілочислових задач і має таку послідовність.

Розв’язування задачі симплекс-методом, не враховуючи вимоги цілочисловості.
Аналіз знайденого розв’язку. Якщо розв’язок цілочисловий, то знайдено оптимальний цілочисловий розв’язок. Якщо хоча б одна базисна змінна не є цілочисловою величиною, то для і-го рядку симплекс-таблиці треба скласти додаткове обмеження.
Складання додаткового обмеження-умови:
- знаходиться дрібова частина вільного члена для всіх рядків

де – ціла частина числа , але менша від самого числа , тобто , наприклад,

вибирається такий 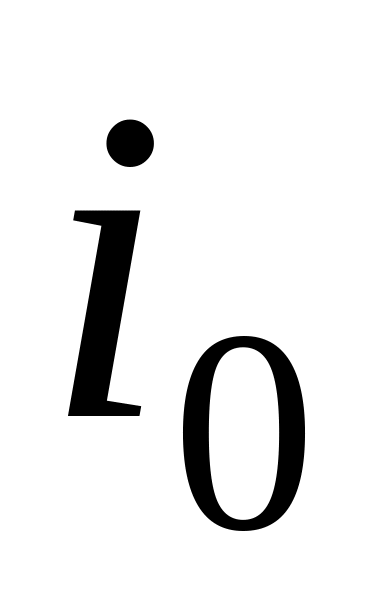-й рядок, для якого

знаходяться дрібові частини коефіцієнтів як

складається додаткове обмеження згідно з формулою

Якщо всі , то задача не має цілочислового розв’язку.

Доповнення початкової математичної моделі задачі додатковим обмеженням, перетворення її до простого виду (якщо це можливо) та перехід до п.1 алгоритму для розв’язування побудованої моделі симплекс-методом.

Треба пам’ятати, що додаткове обмеження доцільно додавати не до початкової моделі, а до симплекс-таблиці знайденого оптимального нецілочислового розв’язку. При цьому треба використовувати двоїстий симплекс-метод, що набагато зменшує обсяг обчислювань. Але для того, щоб використовувати двоїстий симплекс-метод, зручніше початкову модель задачі звести до задачі на мінімум. Це пов’язано з невід’ємністю симплексного відношення, яке може бути тільки при від’ємних оцінках індексного рядку.

У цьому випадку симплексна таблиця оптимального нецілочислового розв’язку доповнюється рядком з базисною змінною :

Це цілком очевидно, якщо додаткове обмеження звести до нерівності типу „ ”, а потім до строгого рівняння за допомогою додаткової змінної .

Побудовану таким чином симплекс-таблицю продовжують розв’язувати двоїстим методом, причому у першу чергу з базису виводиться змінна , тому що для цього рядку .