6.7. Задача управління запасами

Ця задача є характерним прикладом використання методу динамічного програмування, тому що сам процес зміни запасів ресурсів, їх складування та витрати носять часовий розподіл, тобто такий процес є динамічним.

Постановка задачі управління запасами є багатогранна. Розглянемо дискретну задачу з відомими витратами ресурсів у будь-який -й відтинок часу періоду планування .

У цій задачі:

• відомо загальне споживання ресурсів за період , воно дорівнює величині ;

• задано початкові запаси ресурсів, а також попит на ці ресурси на кожному -му відтинку періоду ;

• споживання ресурсів провадиться через склад, де вони зберігаються; витрати на збереження однієї одиниці ресурсів подаються величинами для кожного -го відтинку часу.

Необхідно знайти постачання ресурсів так, щоб цілком задовольнити споживання їх протягом періоду з мінімальними витратами на збереження їх на складі.

Якщо позначити через надходження ресурсів в -й відтинок часу, а наявність ресурсів на складі у кінці -го відтинку часу через , то обмеження математичної моделі мають вигляд:

виконання плану споживання в ресурсах

задоволення попиту на ресурси у будь-який відтинок часу

,

де – загальна величина наявності ресурсів в -й відтинок, а –попит на ці ресурси за цей самий відтинок часу.

Цільова функція має вигляд

Розв’язується задача за функціональним рівнянням

,

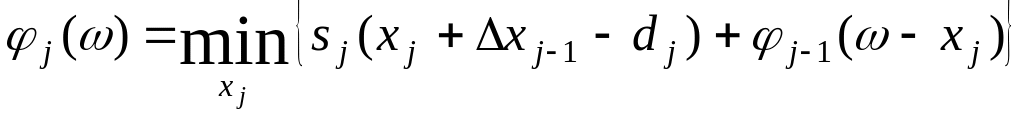де початковий стан складу знаходиться як

,

а величина попиту змінюється від 0 до с дискретним кроком , який дорівнює одній порції попиту ресурсів; величина установлюється у кожному конкретному випадку згідно з сформованими виробничими умовами або точністю розрахунків.

Висновки

1. Метод динамічного програмування використовується для задач, які мають багатокрокову структуру.

2. Метод динамічного програмування дозволяє розв’язувати задачі з заданою цільовою функцією у вигляді таблиць, графіків або діаграм з обов’язковими властивостями адитивності.

3. Обчислювальна процедура методу описується функціональними рівняннями у вигляді рекурентних співвідношень на кожному кроці оптимізації.

4. Розв’язування задач методом динамічного програмування виконується у два етапи:

• побудова таблиці оптимальних розв’язків згідно з рекурентним співвідношенням (етап умовної оптимізації);

• знаходження варіанта розв’язування з таблиці оптимальних розв’язків (етап безумовної оптимізації).

5. Таблиця оптимальних розв’язків дозволяє знаходити оптимальні варіанти для укладених задач, тобто метод дозволяє використовувати таблицю оптимальних розв’язків у випадку зменшення величини та п.

Контрольні запитання

1. Які економічні процеси розглядають моделі задач динамічного програмування?

2. Які переваги має метод динамічного програмування порівняно в іншими методами оптимізації?

3. Вимоги до цільової функції моделі у термінах методу динамічного програмування.

4. Який зміст принципу оптимальності Беллмана і як він враховується у процесі розв’язування задачі?

5. Що передбачає принцип укладення?

6. Як змінюється таблиця оптимальних розв’язків у випадку двосторонніх обмежень на змінні задачі?

7. Як відображується стан об’єкта будь-якого кроку оптимізації, як він розуміється?

8. В яких випадках є альтернативний розв’язок задачі?

РОЗДІЛ 7

ДИСКРЕТНЕ ПРОГРАМУВАННЯ