
- •6.1. Основні властивості задач динамічного програмування та недоліки методу
- •6.2. Загальна математична модель
- •6.3. Розв’язування дискретних задач
- •Рекурентне співвідношення
- •6.3.2. Таблиця оптимальних розв’язків
- •6.3.3. Приклад
- •6.4. Випадок двосторонніх обмежень на змінні
- •6.5. Задачі з багатьма видами ресурсів
- •6.6. Неперервні моделі
- •6.7. Задача управління запасами
- •Висновки
- •Контрольні запитання
- •7.1. Класифікація задач дискретного програмування
- •7.2. Лінійні цілочислові задачі
- •7.2.1. Метод відтинання. Додаткове обмеження
- •7.2.2. Перший алгоритм Гоморі
- •Приклад
- •7.3. Задачі з бульовими змінними
- •7.3.1. Задача про призначення
- •7.3.2. Угорський метод
- •7.3.3. Приклад
- •7.3.4. Задача про кільцевий маршрут
- •Метод розгалужень і меж
- •Початкова матриця
- •7.3.6. Приклад
- •Висновки
- •Контрольні запитання
6.3.2. Таблиця оптимальних розв’язків
Після
завершення розрахунку на усіх п
кроках оптимізації будується таблиця
можливих значень
![]() для будь-яких допустимих значень ресурсів
для будь-яких допустимих значень ресурсів
![]() .
.
Якщо
позначимо через
![]() значення змінної
-го
кроку при стані ресурсів
,
то таблиця оптимальних розв’язків для
всіх допустимих розв’язків задачі має
таку структуру для цілочислових значень:
значення змінної
-го
кроку при стані ресурсів
,
то таблиця оптимальних розв’язків для
всіх допустимих розв’язків задачі має
таку структуру для цілочислових значень:
|
|
|
|
|
... |
|
|
... |
|
|
0 1 2 ...
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Покажемо
у загальному вигляді, як знаходиться
![]() ,
тобто
для ресурсу, який дорівнює
,
тобто
для ресурсу, який дорівнює
![]() .
.
Значення
відповідає другому кроку оптимізації
![]() ,
для якого рекурентне співвідношення
дорівнює:
,
для якого рекурентне співвідношення
дорівнює:
у загальному вигляді
 ,
,
для конкретної величини ресурсу
 .
.
Знайдене
значення
![]() (максимум чи мінімум) заноситься у
таблицю до колонки другого крока
та рядка
поряд з
.
(максимум чи мінімум) заноситься у
таблицю до колонки другого крока
та рядка
поряд з
.
Після проходження усіх п кроків оптимізації згідно з побудованою таблицею можна знайти усі значення змінних , починаючи з останнього п-го кроку, використовуючи формулу
 ,
,
де
![]() – залишки ресурсів на всіх кроках від
першого до
-го,
а
– залишки ресурсів на всіх кроках від
першого до
-го,
а
![]() – кількість ресурсів, що розподілені
з
– кількість ресурсів, що розподілені
з
![]() -го
до останнього
-го
кроку включно.
-го
до останнього
-го
кроку включно.
Слід
підкреслити, що якщо така таблиця
побудована, то можна знайти оптимальний
варіант для всіх значень ресурсів, які
менші від значення
,
тобто для
![]() .
Крім того, з цієї таблиці можна знайти
і всі варіанти розв’язування для задач
з меншою кількістю кроків оптимізації,
тобто для
.
Крім того, з цієї таблиці можна знайти
і всі варіанти розв’язування для задач
з меншою кількістю кроків оптимізації,
тобто для
![]() .
Взагалі кажучи, ці моменти відображують
принцип укладення методу динамічного
програмування.
.
Взагалі кажучи, ці моменти відображують
принцип укладення методу динамічного
програмування.
Отже, у процесі побудови таблиці оптимальних розв’язків знаходиться множина розв’язків задач, що вписуються у розмір основної задачі, тобто є укладеними задачами до задачі більшого розміру.
Звернемо увагу на такий випадок, коли під час побудови таблиці оптимальних розв’язків оптимальна оцінка якогось -го кроку оптимізації з вибраним ресурсом досягається для різних значень . Це вказує на те, що задача має альтернативний оптимум. У цьому випадку для подальшого розв’язування задачі можна брати будь-яке з цих рівноцінних станів об’єкта на -му кроці, або спробувати зробити розрахунки усіх можливих альтернативних розв’язків.
У загальному вигляді значення змінних відповідно таблиці оптимальних розв’язків такі:
п-й
крок: ![]() ,
,
(п
– 1) -й крок: ![]() ,
,
(п
– 2) -й крок: ![]() ,
,
-й
крок : ![]() ,
,
1
- й крок: ![]()
Блок-схема алгоритму розв’язування задачі динамічного програмування дискретного типу наведена на рис.6.3 – 6.4.
Математична
модель

Дискретний
крок

J=1
![]()


![]()


Обчислення
![]()




![]()

=
Знаходження
![]()
Побудова
таблиці для j-го
кроку:
![]()
![]()
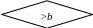
![]()

>
j
= j+1


>
Кінець
побудови таблиці оптимальних розв’язків
Рис. 6.3
Таблиця
оптимальних розв’язків
,
n,
b
![]()

![]()



Вибір
оптимального значення
![]()
Побудова
розв’язку задачі
![]()
![]()
j
= j-1
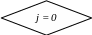

![]()

=
Розв’язок
Рис. 6.4
